Chapter 4.5, Problem 32E

(a)

To determine

To find: The number of complex zeros.

Answer to Problem 32E

2 complex zero

Explanation of Solution

Given information: Analyze the zeros of $f\left(x\right)=x^4-3x^3-2x^2+3x-5$

Calculation:

Descartes Rule tells us that there are either 1 or 3 positive real zeros,

As there are 3 changes of sign

Since $f\left(-x\right)=x^4+3x^3-2x^2-3x-5$

And there is 1 change of sign,

Then there is 1 negative real zero.

If there is 2 positive real zero and 1 negative,

Then there would be 2 complex zero remaining.

(b)

To determine

To list: The possible rational zeros.

Answer to Problem 32E

  $\pm 1,\pm 5$

Explanation of Solution

Given information: Analyze the zeros of $f\left(x\right)=x^4-3x^3-2x^2+3x-5$

Calculation:

Possible rational zeros are every factor of $\frac{5}{1}=\pm 1,\pm 5$

  $\Rightarrow \pm 1,\pm 5$

(c)

To determine

To find: The number of possible positive real zeros and the number of possible negative real zeros.

Answer to Problem 32E

1 or 3 positive real zero, 1 negative real zero

Explanation of Solution

Given information: Analyze the zeros of $f\left(x\right)=x^4-3x^3-2x^2+3x-5$

Calculation:

Descartes Rule tells us that there are either 1 or 3 positive real zeros, as there are 3 changes of sign.

Since $f\left(-x\right)=x^4+3x^3-2x^2-3x-5$ and there is 1 change of sign, then there is 1 negative real zero.

If there is 1 positive real zero a 1 negative, then there would be 2 complex zero remaining.

  

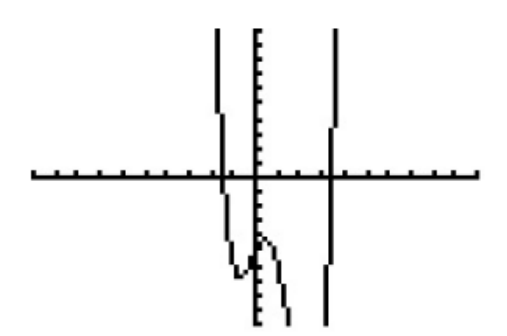
You can see from the graph there is 1 positive and 1 negative real root, leaving 2 complex roots.

(d)

To determine

The integral intervals where the zeros are located.

Answer to Problem 32E

One zero is between $x=-1\text{ and }x=-2$

The 2^nd zero is between $x=3\text{ and }x=4$

Explanation of Solution

Given information: Analyze the zeros of $f\left(x\right)=x^4-3x^3-2x^2+3x-5$

Calculation:

One zero is between $x=-1\text{ and }x=-2$

  

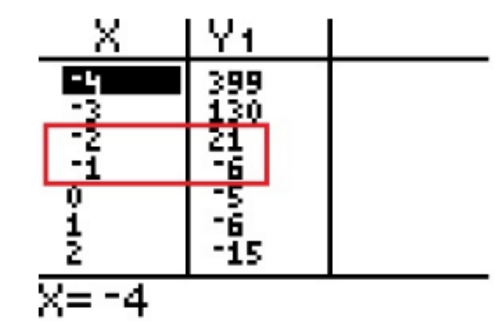
The 2^nd zero is between $x=3\text{ and }x=4$

  

(e)

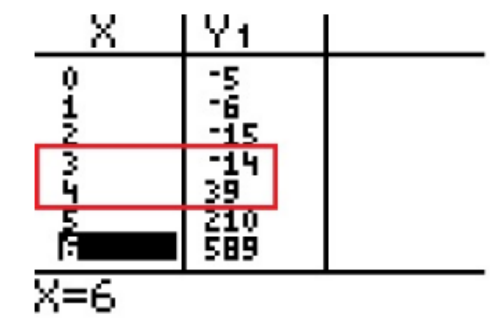
To determine

An integral upper bound of the zeros and an integral lower bound of the zeros.

Answer to Problem 32E

Upper bound: $x=5$

Lower bound: $x=-5$

Explanation of Solution

Given information: Analyze the zeros of $f\left(x\right)=x^4-3x^3-2x^2+3x-5$

Calculation:

$f\left(x\right)=x^4-3x^3-2x^2+3x-5$
r	1 - 3 -2 3 - 5
1	1 - 2 - 4 -1	- 6
5	1 2 8 43	210

Since 5 produces no change in sign in the quotient, then $x=5$ is an upper bound for $f\left(x\right)$ .

$f\left(x\right)=x^4-3x^3-2x^2+3x-5$
r	1 3 -2 3 - 5
1	1 4 2 -1	- 6
5	1 8 38 187	930

Since 5 produces no change in sign in the quotient for $f\left(-x\right)$ , then $x=-5$ is a lower bound for $f\left(x\right)$ .

(f)

To determine

The zeros to the nearest tenth.

Answer to Problem 32E

An approximate zero: $x=-1.4$

An approximate zero: $x=3.4$

Explanation of Solution

Given information: Analyze the zeros of $f\left(x\right)=x^4-3x^3-2x^2+3x-5$

Calculation:

  $f\left(x\right)=x^4-3x^3-2x^2+3x-5$

  

Since − 1.046 is closer to zero than 1.1875, then $x=-1.4$ is an approximate zero.

  

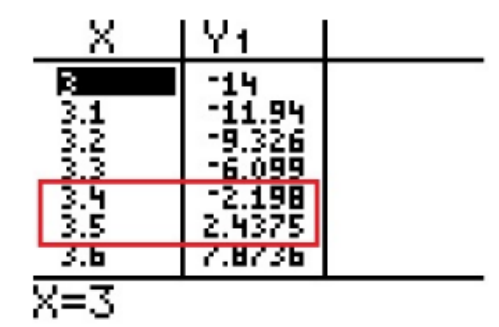
Since − 2.198 is closer to zero than 2.4375, then $x=3.4$ is an approximate zero.