
a.
Write the function for the number of bacteria after 1:00 p.m.
Given information:
The exponential function
At
Concept Used:
Substitute the value of a
Calculation:
As per the given problem
Note that for this problem the starting population
Now the working equation for this problem,
Conclusion:
Hence, the equation is
b.
Graph the function
The graph is in the solution
Given:
The exponential function
At
Concept Used:
Draw the graph Substitute the value of a
.Graph:
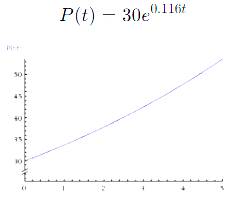
Conclusion:
Hence, the graph is above in the solution.
c.
Write the population at 5:00 P.M.
Given:
The exponential function
Concept Used:
Substitute the value of a
Calculation:
As per the given problem
Note that for 5:00 P.M that would be
Now the working equation for this problem,
Conclusion:
Hence, the population at 5:00 pm
d.
How to find the population at 3:45 P.M.
Given:
The exponential function
Concept Used:
Substitute the value of a
Calculation:
As per the given problem
Note that for 5:00 P.M that would be
Now the working equation for this problem,
Graph the function
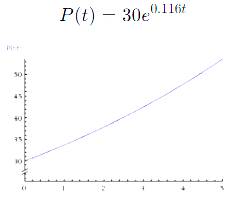
Now to find the population at
For the equation, time needs to be in hours so this would convert to
Now plug it in and do the math or a less
Conclusion:
To find the population at 3:45 pm read answer above.
Chapter 4 Solutions
EBK ALGEBRA 2
- Thank you.arrow_forwardThank you.arrow_forwardLet V, W, and Y be vector spaces. Suppose dim(V) dim(W) = dim(Y) = 2. = Let ("beta") be an ordered basis for V. Let ("gamma") be an ordered basis for W. Let ("zeta") be an ordered basis for Y. Suppose S is a linear transformation from V to W and that T is a linear trans- formation from W to Y. Remember that ToS is the function from V to Y defined by (TOS)(v) = T(S(v)). (a) Prove that To S is a linear transformation. (b) Prove that ° [T • S] = [T]{[S]}.arrow_forward
- Let W={(0, a, 0) | a Є R}. (a) List four elements from W. (b) Determine whether W is a subspace of R³, and prove that your answer is correct.arrow_forwardFor this problem, refer to the network as shown in Figure 1, answer the following questions. B A C FIGURE 1. For Problem (7). Let x₁ be the number of users at website A. Let x2 be the number of users at website B. Let x3 be the number of users at website C. Assume that there are a total of 900 users at these three websites. This gives us the following system of linear equations: x1 = x2 + 1x3 x2 = x1 + x3 x3 = x2 = 900 x1 + x2 + x3 = (a) Put this system into a standard form (with all variables on the left side and with the constants on the right), and convert that system into an augmented matrix, and then... (b) Use elementary row operations to put the augmented matrix into reduced row echelon form, and then... (c) Write down the solution space for this system of equations, and then... (d) Identify which website(s) would be ranked most highly by PageRank.arrow_forward4 2 Let C = -6 -3 (a) Find det(C). (b) Use your answer for (a) to determine whether C is invertible.arrow_forward
 Algebra and Trigonometry (6th Edition)AlgebraISBN:9780134463216Author:Robert F. BlitzerPublisher:PEARSON
Algebra and Trigonometry (6th Edition)AlgebraISBN:9780134463216Author:Robert F. BlitzerPublisher:PEARSON Contemporary Abstract AlgebraAlgebraISBN:9781305657960Author:Joseph GallianPublisher:Cengage Learning
Contemporary Abstract AlgebraAlgebraISBN:9781305657960Author:Joseph GallianPublisher:Cengage Learning Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning Algebra And Trigonometry (11th Edition)AlgebraISBN:9780135163078Author:Michael SullivanPublisher:PEARSON
Algebra And Trigonometry (11th Edition)AlgebraISBN:9780135163078Author:Michael SullivanPublisher:PEARSON Introduction to Linear Algebra, Fifth EditionAlgebraISBN:9780980232776Author:Gilbert StrangPublisher:Wellesley-Cambridge Press
Introduction to Linear Algebra, Fifth EditionAlgebraISBN:9780980232776Author:Gilbert StrangPublisher:Wellesley-Cambridge Press College Algebra (Collegiate Math)AlgebraISBN:9780077836344Author:Julie Miller, Donna GerkenPublisher:McGraw-Hill Education
College Algebra (Collegiate Math)AlgebraISBN:9780077836344Author:Julie Miller, Donna GerkenPublisher:McGraw-Hill Education





