Chapter 4.2, Problem 31PS

Solution

a.

To find: The model that gives the value of the mountain bike $y$ (in dollars) after $t$ years.

The model representing the value of the mountain bike after $t$ years is $y=200{\left(0.75\right)}^t$ .

The value of the bike after 3 years is $84.375.

Given:

The cost of a new mountain bike is $200.

Its value decreases by 25% each year.

Calculation:

Here, the initial cost is

  $a=\$200$

And, the decay rate is

  $\begin{array}{c}r=\frac{25}{100}\\ =0.25\end{array}$

Now the model is,

  $\begin{array}{l}y=a{\left(1-r\right)}^t\\ y=200{\left(1-0.25\right)}^t\\ y=200{\left(0.75\right)}^t\end{array}$

Hence, the model representing the value of the mountain bike after $t$ years is $y=200{\left(0.75\right)}^t$ .

Now, the value of the bike after 3 years is

  $\begin{array}{c}y=200{\left(0.75\right)}^3\\ =\$84.375\end{array}$

Hence, the value of the bike after 3 years is $84.375.

b.

To draw: The graph of the model.

  

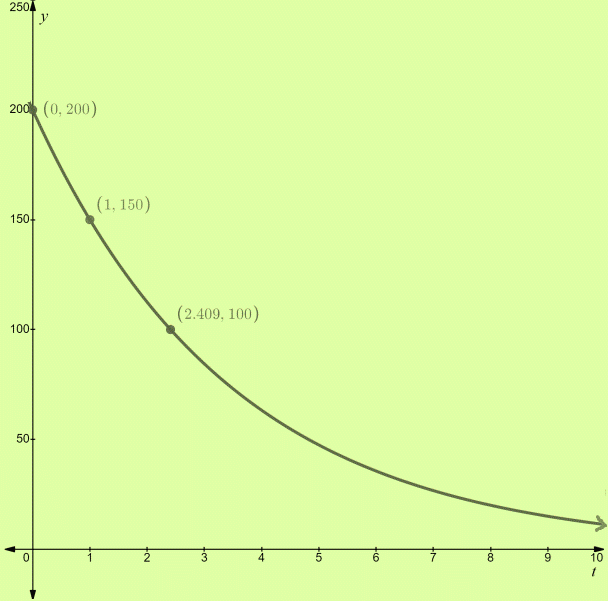
Given:

  $y=200{\left(0.75\right)}^t$

Calculation:

The graph of this model passes through the points $\left(0,200\right),\left(1,150\right)$ .

Now the graph is,

  

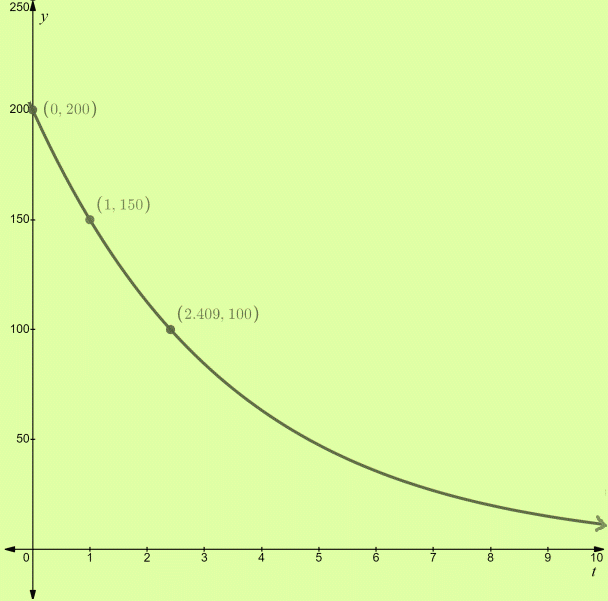
c.

To estimate: When the value of the bike is $100.

The value of a mountain bike is $100 after about 2 years.

Given:

  $y=200{\left(0.75\right)}^t$

Calculation:

From the graph in subpart (b), it can be seen that the value of a bike will be $100 after about 2 years.

Hence, the value of a mountain bike is $100 after about 2 years.