Chapter 4.2, Problem 85E

(a)

To determine

Find the symmetry of the points $(x_{1,}{y}_1)$ and $(x_{2,}{y}_2)$ .

Answer to Problem 85E

y − axis symmetry.

Explanation of Solution

Given: Draw two points $(x_{1,}{y}_1)$ and $(x_{2,}{y}_2)$ on the unit circle corresponding to $t=t_1$ and $t=\text{π}-t_1$ respectively.

Concept Used:

 Mathematically, symmetry means that one shape becomes exactly like another when you move it in some way: turn, flip or slide. For two objects to be symmetrical, they must be the same size and shape, with one object having a different orientation from the first. There can also be symmetry in one object, such as a face. If you draw a line of symmetry down the centre of your face, you can see that the left side is a mirror image of the right side. Not all objects have symmetry; if an object is not symmetrical, it is called asymmetric

Calculation:

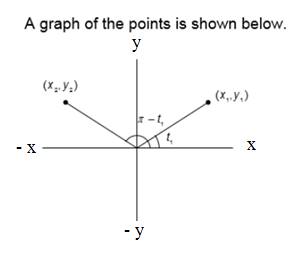Let $(x_{1,}{y}_1)$ and $(x_{2,}{y}_2)$ on the unit circle corresponding to $t=t_1$ and $t=\text{π}-t_1$respectively.   $\begin{array}{l}{x}_1=\cos t_1;y_1=\sin t_1\\ $ x_2=\cos {(\text{π}-t_1)}_1;y_2=\sin (\text{π}-t_1)$\end{array}$ And the both points are reflection of each other with respect to y − axis Therefore they are related as $(x_2,y_2)=(-x_1,y_1)$. Hence the points are Y − axis symmetry.

Thus, the points are y − axis symmetry.

(b)

To determine

Make a conjecture about any relationship between $\sin t_1$ and $\sin (\text{π}-t_1)$

Answer to Problem 85E

  $\sin t_1=\sin (\text{π}-t_1)$

Explanation of Solution

Given: Draw two points $(x_{1,}{y}_1)$ and $(x_{2,}{y}_2)$ on the unit circle corresponding to $t=t_1$ and $t=\text{π}-t_1$ respectively.

Concept Used:

The line (or "axis") of symmetry is the y-axis, also known as the line x = 0. This line is marked green in the picture. The graph is said to be "symmetric about the y-axis", and this line of symmetry is also called the "axis of symmetry" 

Calculation:

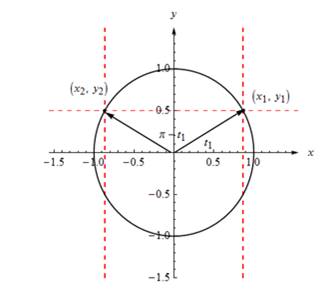Draw two points$(x_{1,}{y}_1)$ and $(x_{2,}{y}_2)$ on the unit circle corresponding to $t=t_1$ and $t=\text{π}-t_1$respectively. $\begin{array}{l}{x}_1=\cos t_1;y_1=\sin t_1\\ $ x_2=\cos {(\text{π}-t_1)}_1;y_2=\sin (\text{π}-t_1)$\end{array}$ And the both points are reflection of each other with respect to y − axis Therefore they are related as $(x_2,y_2)=(-x_1,y_1)$. Now we can see the points $(x_{1,}{y}_1)$ and $(x_{2,}{y}_2)$ are in y − axis symmetry. Since the graph has symmetry to the y − axis, the y − coordinates are the same which means $\sin t_1=\sin (\text{π}-t_1)$

Thus, $\sin t_1=\sin (\text{π}-t_1)$

(c)

To determine

Make a conjecture about any relationship between $\cos t_1$ and $\cos (\text{π}-t_1)$

Answer to Problem 85E

  $\cos t_1=-\cos (\text{π}-t_1)$

Explanation of Solution

Given:

Draw two points $(x_{1,}{y}_1)$ and $(x_{2,}{y}_2)$ on the unit circle corresponding to $t=t_1$ and $t=\text{π}-t_1$ respectively.

Concept Used:

The line (or "axis") of symmetry is the y-axis, also known as the line x = 0. This line is marked green in the picture. The graph is said to be "symmetric about the y-axis", and this line of symmetry is also called the "axis of symmetry" 

Calculation:

Draw two points $(x_{1,}{y}_1)$ and $(x_{2,}{y}_2)$ on the unit circle corresponding to $t=t_1$ and $t=\text{π}-t_1$ respectively. $\begin{array}{l}{x}_1=\cos t_1;y_1=\sin t_1\\ $ x_2=\cos {(\text{π}-t_1)}_1;y_2=\sin (\text{π}-t_1)$\end{array}$ And the both points are reflection of each other with respect to y − axis Therefore they are related as $(x_2,y_2)=(-x_1,y_1)$. Now we can see the points $(x_{1,}{y}_1)$ and $(x_{2,}{y}_2)$ are in y − axis symmetry. Since the graph has symmetry to the y − axis, the y − coordinatesare the same but the x − coordinatesare in opposite sign which means   $\cos t_1=-\cos (\text{π}-t_1)$

Thus, $\cos t_1=-\cos (\text{π}-t_1)$