Chapter 4.1, Problem 3P

a.

To determine

To graph: showing the height with respect to time.

Explanation of Solution

Given:

A person starts swinging from the ground, then attains a maximum height and then slows down until the swing stops.

Concept used:

Given example is of a damped oscillation where the swing is oscillating between its amplitude and due to damping force, its amplitude is continuously decreasing.

For a simple oscillation without damping the equation is $y=a\sin (\omega t)$

But as stated the height of the swing will first increase meaning that the amplitude will increase and then decrease, thus there will be 2 parts of the graph, one with increasing amplitude and one with decreasing amplitude.

The equation of graph for the part when swing starts from the ground and increases its amplitude will be $y=e^{-0.4t}\cos \left(9t\right)$ .

Here it must be noted that the power of eand value of $\omega$ is decided as arbitrarily so as to facilitate a easily observable graph.

Thus the graph formed is given below.

Graph:

  

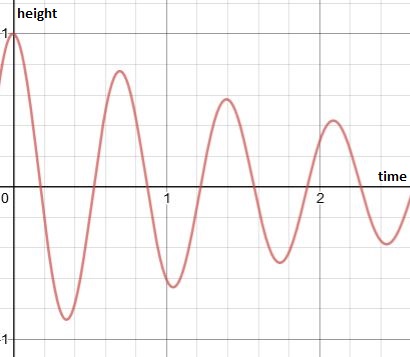
Interpretation:

The height of the swing gradually increases from 0 up to maximum height while passing through the mean position every time.

Here height at 0 doesn’t mean ground level but the mean height from the ground

Now, for the second part of the graph where the height of the swing decreases gradually until it stop, the equation will have cosine function as it starts from maximum value and ends at 0

So the equation for this graph will be $y=e^{-0.4t}\cos \left(9t\right)$ .

Conclusion:

The height of swing will decrease gradually because of the damped forces acting such as friction. Eventually the height becomes zero and the swing stops.

b.

To determine

To find: the change in the graph if instead of slowing down the person jumps from the swing.

Answer to Problem 3P

A parabola will be formed

Explanation of Solution

Given:

A person is swingfrom any point from him, and jumps to land on the ground.

Concept used:

When the person is swinging, he already has some momentum because of the motion of the swing.

If he jumps from the swing at any point he will follow a parabolic path because of his velocity in horizontal direction and due to the gravitational force in vertical direction

Due to the momentum the person will be launched into air from the swing and he will follow a parabolic path.

Graph:

The 1^st part of graph will be similar as there are no changes while speeding up but the second part of graph will be different as given below.

  

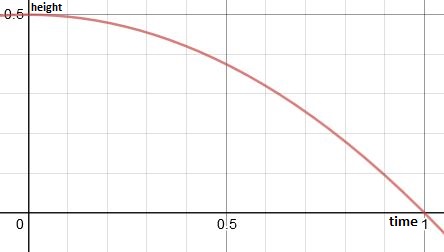
Conclusion:

If the person jumps from the swing mid-air instead of slowing down, he follows a trajectory of a parabola.