
Concept explainers
(a)
The acceleration of the objects and the tension in the string in terms of
(a)
Answer to Problem 75P
The expression for the tension in the string is
Explanation of Solution
Calculation:
The free body diagram for the blocks is shown in Figure 1
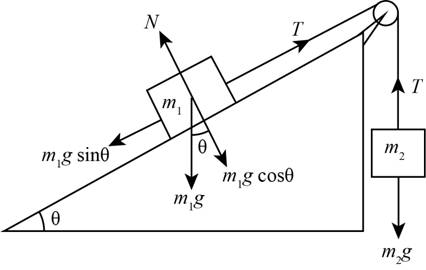
Figure 1
Consider the tension in the string is
The expression for the tension
The expression for the tension in terms of the acceleration for mass
The expression for the tension
The expression for the tension in terms of the acceleration for mass
The expression for the acceleration is evaluated as,
The expression for the tension in terms of acceleration is given by,
Conclusion:
Therefore, the expression for the tension in the string is
(b)
The acceleration and the tension of the string.
(b)
Answer to Problem 75P
The tension of the string is
Explanation of Solution
Given:
The angle of inclination is
The mass of first block is
The mass of the second block is
Calculation:
The acceleration of the string is calculated as,
The tension in the string is calculated as,
Conclusion:
Therefore, the tension of the string is
Want to see more full solutions like this?
Chapter 4 Solutions
EBK PHYSICS FOR SCIENTISTS AND ENGINEER
- Two conductors having net charges of +14.0 µC and -14.0 µC have a potential difference of 14.0 V between them. (a) Determine the capacitance of the system. F (b) What is the potential difference between the two conductors if the charges on each are increased to +196.0 µC and -196.0 µC? Varrow_forwardPlease see the attached image and answer the set of questions with proof.arrow_forwardHow, Please type the whole transcript correctly using comma and periods as needed. I have uploaded the picture of a video on YouTube. Thanks,arrow_forward
- A spectra is a graph that has amplitude on the Y-axis and frequency on the X-axis. A harmonic spectra simply draws a vertical line at each frequency that a harmonic would be produced. The height of the line indicates the amplitude at which that harmonic would be produced. If the Fo of a sound is 125 Hz, please sketch a spectra (amplitude on the Y axis, frequency on the X axis) of the harmonic series up to the 4th harmonic. Include actual values on Y and X axis.arrow_forwardSketch a sign wave depicting 3 seconds of wave activity for a 5 Hz tone.arrow_forwardSketch a sine wave depicting 3 seconds of wave activity for a 5 Hz tone.arrow_forward
- The drawing shows two long, straight wires that are suspended from the ceiling. The mass per unit length of each wire is 0.050 kg/m. Each of the four strings suspending the wires has a length of 1.2 m. When the wires carry identical currents in opposite directions, the angle between the strings holding the two wires is 20°. (a) Draw the free-body diagram showing the forces that act on the right wire with respect to the x axis. Account for each of the strings separately. (b) What is the current in each wire? 1.2 m 20° I -20° 1.2 marrow_forwardplease solve thisarrow_forwardplease solve everything in detailarrow_forward
- 6). What is the magnitude of the potential difference across the 20-02 resistor? 10 Ω 11 V - -Imm 20 Ω 10 Ω 5.00 10 Ω a. 3.2 V b. 7.8 V C. 11 V d. 5.0 V e. 8.6 Varrow_forward2). How much energy is stored in the 50-μF capacitor when Va - V₁ = 22V? 25 µF b 25 µF 50 µFarrow_forward9). A series RC circuit has a time constant of 1.0 s. The battery has a voltage of 50 V and the maximum current just after closing the switch is 500 mA. The capacitor is initially uncharged. What is the charge on the capacitor 2.0 s after the switch is closed? R 50 V a. 0.43 C b. 0 66 C c. 0.86 C d. 0.99 C Carrow_forward
 Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill
Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University
University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning Classical Dynamics of Particles and SystemsPhysicsISBN:9780534408961Author:Stephen T. Thornton, Jerry B. MarionPublisher:Cengage Learning
Classical Dynamics of Particles and SystemsPhysicsISBN:9780534408961Author:Stephen T. Thornton, Jerry B. MarionPublisher:Cengage Learning Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning





