Chapter 4, Problem 4.152RP

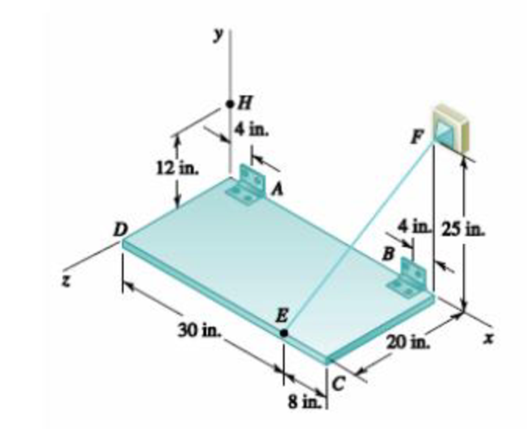
The rectangular plate shown weighs 75 lb and is held in the position shown by hinges at A and B and by cable EF. Assuming that the hinge at B does not exert any axial thrust, determine (a) the tension in the cable, (b) the reactions at A and B.

To determine

The tension in the cable.

Answer to Problem 4.152RP

The tension in the cable is $49.5\text{ lb}$ .

Explanation of Solution

The free-body diagram is shown in figure 1.

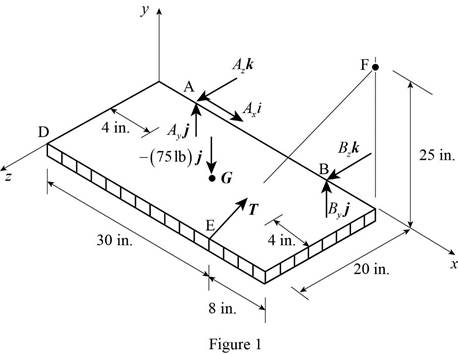
Write the expression for the tension in the cable.

$\overrightarrow{T}=T\frac{\overrightarrow{EF}}{EF}$ (I)

Here, $\overrightarrow{T}$  is the tension in the cable and $T$ is the magnitude of $\overrightarrow{T}$ .

Write the expression of the vector $\overrightarrow{EF}$ .

$\overrightarrow{EF}=\left(8\text{ in}\right)\widehat{i}+\left(25\text{ in}\right)\widehat{j}-\left(20\text{ in}\right)\widehat{k}$ (II)

Find the magnitude of the vector $\overrightarrow{EF}$ .

$\begin{array}{c}EF=\sqrt{{\left(8\text{ in}\right)}^2+{\left(25\text{ in}\right)}^2+{\left(-20\text{ in}\right)}^2}\\ =33\text{ in}\end{array}$ (III)

Put equations (II) and (III) in equation (I).

$\begin{array}{c}\overrightarrow{T}=T\frac{\left(8\text{ in}\right)\widehat{i}+\left(25\text{ in}\right)\widehat{j}-\left(20\text{ in}\right)\widehat{k}}{33\text{ in}}\\ =\frac{T}{33}\left(8\widehat{i}+25\widehat{j}-20\widehat{k}\right)\end{array}$ (IV)

Write the expressions for the position vectors.

$\begin{array}{c}{\overrightarrow{r}}_{B/A}=\left(38-8\right)\widehat{i}\\ =30\widehat{i}\\ {\overrightarrow{r}}_{E/A}=\left(30-4\right)\widehat{i}+20\widehat{k}\\ =26\widehat{i}+20\widehat{k}\\ {\overrightarrow{r}}_{G/A}=\frac{38}{2}\widehat{i}+10\widehat{k}\\ =19\widehat{i}+10\widehat{k}\end{array}$ (V)

Here, ${\overrightarrow{r}}_{B/A}$ , ${\overrightarrow{r}}_{E/A}$ and ${\overrightarrow{r}}_{G/A}$ are position vectors.

Sum of the moments of the forces about the point A must be zero.

$\Sigma M_A=0$ (VI)

Here, $\Sigma M_A$ is the sum of the moments of forces about the point A.

Write the expression for the sum of the moments about the point A.

$\Sigma M_A={\overrightarrow{r}}_{E/A}\times T+{\overrightarrow{r}}_{G/A}\times \left(-75\widehat{j}\right)+{\overrightarrow{r}}_{B/A}\times B$

Here, $\overrightarrow{B}$ is the reaction at the point B.

Put the above equation in equation (VI) and use determinants.

$\begin{array}{c}{\overrightarrow{r}}_{E/A}\times T+{\overrightarrow{r}}_{G/A}\times \left(-75\widehat{j}\right)+{\overrightarrow{r}}_{B/A}\times B=0\\ \left|\begin{array}{ccc}\widehat{i}& \widehat{j}& \widehat{k}\\ 26& 0& 20\\ 8& 25& -20\end{array}\right|\frac{T}{33}+\left|\begin{array}{ccc}\widehat{i}& \widehat{j}& \widehat{k}\\ 19& 0& 10\\ 0& -75& 0\end{array}\right|+\left|\begin{array}{ccc}\widehat{i}& \widehat{j}& \widehat{k}\\ 30& 0& 0\\ 0& {\overrightarrow{B}}_y& {\overrightarrow{B}}_z\end{array}\right|=0\end{array}$ (VII)

Conclusion:

Equate the coefficient of $\widehat{i}$ in equation (VII) to zero.

$\begin{array}{c}-\left(25\right)\left(20\right)\frac{T}{33}+750=0\\ T=\frac{\left(750\right)\left(33\right)}{500}\\ =49.5\text{ lb}\end{array}$

Thus, the tension in the cable is $49.5\text{ lb}$ .

To determine

The reactions at A and B.

Answer to Problem 4.152RP

The reaction at A is $-\left(12.00\text{ lb}\right)\widehat{i}+\left(22.5\text{ lb}\right)\widehat{j}-\left(4.00\text{ lb}\right)\widehat{k}$ and the reaction at B is $\left(15.00\text{ lb}\right)\widehat{j}+\left(34.0\text{ lb}\right)\widehat{k}$.

Explanation of Solution

Equate the coefficient of $\widehat{j}$ in equation (VII) to zero.

$\left(160+520\right)\frac{T}{33}-30B_z=0$

Here, $B_z$ is the $z$ component of $\overrightarrow{B}$ .

Substitute $49.5\text{ lb}$ for $T$ in the above equation to find $B_z$ .

$\begin{array}{c}\left(160+520\right)\frac{49.5\text{ lb}}{33}-30B_z=0\\ B_z=\frac{\left(680\right)49.5\text{ lb}}{\left(33\right)\left(30\right)}\\ =34\text{ lb}\end{array}$

Equate the coefficient of $\widehat{k}$ in equation (VII) to zero.

$\left(26\right)\left(25\right)\frac{T}{33}-1425+30B_y=0$

Here, $B_y$ is the $y$ component of $\overrightarrow{B}$ .

Substitute $49.5\text{ lb}$ for $T$ in the above equation to find $B_y$ .

$\begin{array}{c}{B}_y=\frac{1}{30}\left(1425-\left(26\right)\left(25\right)\frac{49.5\text{ lb}}{33}\right)\\ =15\text{ lb}\end{array}$

Write the expression for $\overrightarrow{B}$.

$\overrightarrow{B}=B_y\widehat{j}+B_z\widehat{k}$

Substitute $34\text{ lb}$ for $B_z$ and $15\text{ lb}$ for $B_y$ in the above equation to find $\overrightarrow{B}$ .

$\overrightarrow{B}=\left(15\text{ lb}\right)\widehat{j}+\left(34\text{ lb}\right)\widehat{k}$

Refer figure 1.

The net force must be equal to zero.

$\Sigma F=0$ (VIII)

Here, $\Sigma F$ is the net force.

Write the expression for the net force.

$\Sigma F=\overrightarrow{A}+\overrightarrow{B}+\overrightarrow{T}-\left(75\text{ lb}\right)\widehat{j}$

Here, $\overrightarrow{A}$ is the reaction at the point A.

Put the above equation in equation (VIII).

$\begin{array}{c}\overrightarrow{A}+\overrightarrow{B}+\overrightarrow{T}-\left(75\text{ lb}\right)\widehat{j}=0\\ \left(A_x\widehat{i}+A_y\widehat{j}+A_z\widehat{k}\right)+\left(B_y\widehat{j}+B_z\widehat{k}\right)+\left(T_x\widehat{i}+T_y\widehat{j}+T_z\widehat{k}\right)-\left(75\text{ lb}\right)\widehat{j}=0\\ \left(A_x\widehat{i}+A_y\widehat{j}+A_z\widehat{k}\right)+\left(15\text{ lb}\right)\widehat{j}+\left(34\text{ lb}\right)\widehat{k}+\frac{49.5\text{ lb}}{33}\left(8\widehat{i}+25\widehat{j}-20\widehat{k}\right)-\left(75\text{ lb}\right)\widehat{j}=0\end{array}$ (IX)

Equate the coefficient of $\widehat{i}$ in equation (IX) to zero.

$\begin{array}{c}{A}_x+\frac{8}{33}\left(49.5\right)=0\\ A_x=-12.00\text{ lb}\end{array}$

Equate the coefficient of $\widehat{j}$ in equation (IX) to zero.

$\begin{array}{c}{A}_y+15+\frac{25}{33}\left(49.5\right)-75=0\\ A_y=75-15-\frac{25}{33}\left(49.5\right)\\ =22.5\text{ lb}\end{array}$

Equate the coefficient of $\widehat{k}$ in equation (IX) to zero.

$\begin{array}{c}{A}_z+34-\frac{20}{33}\left(49.5\right)=0\\ A_z=\frac{20}{33}\left(49.5\right)-34\\ =-4.00\text{ lb}\end{array}$

Write the expression of $\overrightarrow{A}$ .

$\overrightarrow{A}=-\left(12.00\text{ lb}\right)\widehat{i}+\left(22.5\text{ lb}\right)\widehat{j}-\left(4.00\text{ lb}\right)\widehat{k}$

Conclusion:

Thus, the reaction at A is $-\left(12.00\text{ lb}\right)\widehat{i}+\left(22.5\text{ lb}\right)\widehat{j}-\left(4.00\text{ lb}\right)\widehat{k}$ and the reaction at B is $\left(15.00\text{ lb}\right)\widehat{j}+\left(34.0\text{ lb}\right)\widehat{k}$.