
Table 3.P.1 lists drug concentration measurements made in blood and tissue compartments over a period of
TABLE 3.P.1 Compartment concentration measurements.
Estimating Eigenvalues and Eigenvectors of
respectively. The solution of Eq. (1) can be expressed as
where
(a) For values of
Given that both components of the data
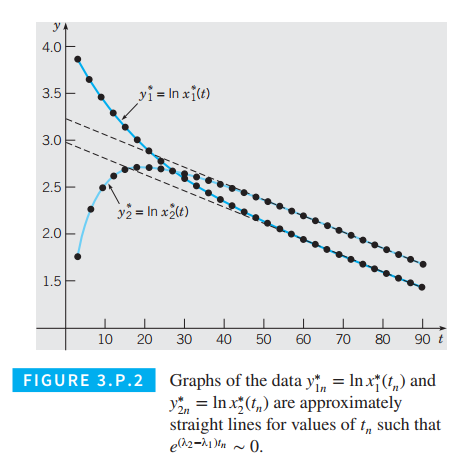
Computing the Entries of
and
or, using matrix notation,
Given estimates
Want to see the full answer?
Check out a sample textbook solution
Chapter 3 Solutions
DIFFERENTIAL EQUATIONS-NEXTGEN WILEYPLUS
Additional Math Textbook Solutions
Pre-Algebra Student Edition
Calculus for Business, Economics, Life Sciences, and Social Sciences (14th Edition)
Basic Business Statistics, Student Value Edition
A Problem Solving Approach To Mathematics For Elementary School Teachers (13th Edition)
A First Course in Probability (10th Edition)
Intro Stats, Books a la Carte Edition (5th Edition)
- pls helparrow_forwardQ1: A: Let M and N be two subspace of finite dimension linear space X, show that if M = N then dim M = dim N but the converse need not to be true. B: Let A and B two balanced subsets of a linear space X, show that whether An B and AUB are balanced sets or nor. Q2: Answer only two A:Let M be a subset of a linear space X, show that M is a hyperplane of X iff there exists ƒ€ X'/{0} and a € F such that M = (x = x/f&x) = x}. fe B:Show that every two norms on finite dimension linear space are equivalent C: Let f be a linear function from a normed space X in to a normed space Y, show that continuous at x, E X iff for any sequence (x) in X converge to Xo then the sequence (f(x)) converge to (f(x)) in Y. Q3: A:Let M be a closed subspace of a normed space X, constract a linear space X/M as normed space B: Let A be a finite dimension subspace of a Banach space X, show that A is closed. C: Show that every finite dimension normed space is Banach space.arrow_forwardpls helparrow_forward
 Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
