
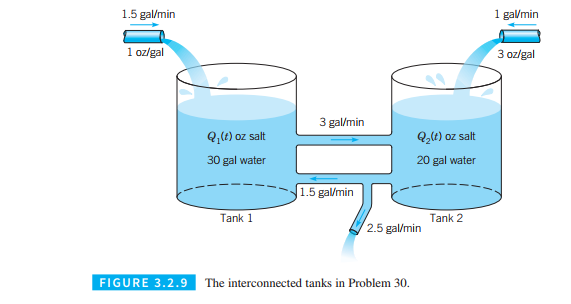
Consider two interconnected tanks similar to those on Figure 3.2.9. Tank
(a) Draw a diagram that depicts the flow process described above. Let
(b) Find the equilibrium values
(c) Is it possible (by adjusting
(d) Describe which equilibrium states are possible for this system for various values of
Want to see the full answer?
Check out a sample textbook solution
Chapter 3 Solutions
DIFFERENTIAL EQUATIONS-NEXTGEN WILEYPLUS
Additional Math Textbook Solutions
Elementary Statistics Using The Ti-83/84 Plus Calculator, Books A La Carte Edition (5th Edition)
Thinking Mathematically (6th Edition)
Calculus for Business, Economics, Life Sciences, and Social Sciences (14th Edition)
Intro Stats, Books a la Carte Edition (5th Edition)
Elementary Statistics (13th Edition)
- Problem 5 ( Marybeth is also interested in the experiment from Problem 2 (associated with the enhancements for Captain America's shield), so she decides to start a detailed literature review on the subject. Among others, she found a paper where they used a 2"(4-1) fractional factorial design in the factors: (A) shield material, (B) throwing mechanism, (C) edge modification, and (D) handle adjustment. The experimental design used in the paper is shown in the table below. a. Run A B с D 1 (1) -1 -1 -1 1 2 a 1 -1 -1 1 3 bd -1 1 -1 1 4 abd 1 1 -1 1 5 cd -1 -1 1 -1 6 acd 1 -1 1 -1 7 bc -1 1 1 -1 abc 1 1 1 -1 paper? s) What was the generator used in the 2"(4-1) fractional factorial design described in the b. Based on the resolution of this design, what do you think about the generator used in the paper? Do you think it was a good choice, or would you have selected a different one? Explain your answer in detail.arrow_forwardNot use ai pleasearrow_forwardIn the xy-plane, an angle 0, in standard position, has a measure of the following is true? T. Which of 3 A The slope of the terminal ray of the angle is 1. B The slope of the terminal ray of the angle is 1. C D 3 The slope of the terminal ray of the angle is ✓ 2 The slope of the terminal ray of the angle is √3.arrow_forward
- y'''-3y''+4y=e^2x Find particular solutionarrow_forwardNo chatgpt pls will upvote Already got wrong chatgpt answer Plzarrow_forward1 -1- Ο Graph of f y = + y = 1 + 1/2 ·2· x Graph of g y = 1- 플 The figure gives the graphs of the functions f and g in the xy-plane. The function of is given by f(x) = tan¹ x. Which of the following defines g(x)? A tan 1 x + 1 B - tan 1 x + П 2 C tan-1 (2/2) + 1 D tan-1 (2/2) + 1/1arrow_forward
- In Problems 10-4, use the method of undetermined coefficients to determine the form of a particular solution for the given equation.arrow_forwardIn Problems 10-40, use the method of undetermined coefficients to determine the form of a particular solution for the given equation. 2 1. y"" - 2y" - 5y/+6y= e² + x²arrow_forwardmatch the equation to it's respective directional field in the image, justify your answer a. dy/dx=x-1 b. dy/dx=1 - y^2 c. dy/dx=y^2 - x^2 d. dy/dx=1-x e. dy/dx=1-y f. dy/dx=x^2 - y^2 g. dy/dx=1+y h. dy/dx=y^2 - 1arrow_forward
- 4. The runway at the Piarco International airport has an equation of -3(x-2y) = 6. If the Priority Bus Route passes through the geometric coordinate (1,-9) and is perpendicular to the runway at the Piarco International airport. Determine the following: a. State two geometric coordinates which the runway at the Piarco International airport passes through. b. Derive the equation of the Priority Bus Route. [2 marks] [6 marks]arrow_forwardUse Euler and Heun methods to solve y' = 2y-x, h=0.1, y(0)=0, compute y₁ys, calculate the Abs_Error.arrow_forwardTY D om E h om ng 00 C B A G F Q ו 3 13 Details Find an Euler path for the graph. Enter your response as a sequence of vertices in the order they are visited, for example, ABCDEA. fic ► Question Help: Video Message instructor Submit Question tor arch 園 A Wind advisoryarrow_forward
 Discrete Mathematics and Its Applications ( 8th I...MathISBN:9781259676512Author:Kenneth H RosenPublisher:McGraw-Hill Education
Discrete Mathematics and Its Applications ( 8th I...MathISBN:9781259676512Author:Kenneth H RosenPublisher:McGraw-Hill Education Mathematics for Elementary Teachers with Activiti...MathISBN:9780134392790Author:Beckmann, SybillaPublisher:PEARSON
Mathematics for Elementary Teachers with Activiti...MathISBN:9780134392790Author:Beckmann, SybillaPublisher:PEARSON
 Thinking Mathematically (7th Edition)MathISBN:9780134683713Author:Robert F. BlitzerPublisher:PEARSON
Thinking Mathematically (7th Edition)MathISBN:9780134683713Author:Robert F. BlitzerPublisher:PEARSON Discrete Mathematics With ApplicationsMathISBN:9781337694193Author:EPP, Susanna S.Publisher:Cengage Learning,
Discrete Mathematics With ApplicationsMathISBN:9781337694193Author:EPP, Susanna S.Publisher:Cengage Learning, Pathways To Math Literacy (looseleaf)MathISBN:9781259985607Author:David Sobecki Professor, Brian A. MercerPublisher:McGraw-Hill Education
Pathways To Math Literacy (looseleaf)MathISBN:9781259985607Author:David Sobecki Professor, Brian A. MercerPublisher:McGraw-Hill Education





