Differential Equations: Computing and Modeling (5th Edition), Edwards, Penney & Calvis
5th Edition
ISBN: 9780321816252
Author: C. Henry Edwards, David E. Penney, David Calvis
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 3.7, Problem 4P
Problems 1 through 6 deal with the RL circuit of Fig. 3.7.7, a series circuit containing an inductor with an inductance of L henries, a resistor with a resistance of R ohms, and a source of electromotive force (emf), but no capacitor In this case Eq. (2) reduces to the linear first-order equation FIGURE 3.7.7. The circuit for Problems 1 through 6.
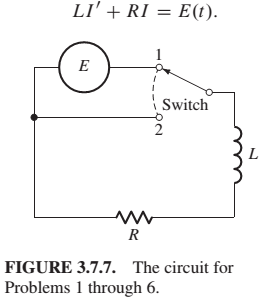
In the circuit of Fig. 3.7.7, with the switch in position 1, suppose that
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Please answer the JAVA OOP Programming Assignment scenario below:
Patriot Ships is a new cruise line company which has a fleet of 10 cruise ships, each with a capacity of 300 passengers. To manage its operations efficiently, the company is looking for a program that can help track its fleet, manage bookings, and calculate revenue for each cruise.
Each cruise is tracked by a Cruise Identifier (must be 5 characters long), cruise route (e.g. Miami to Nassau), and ticket price. The program should also track how many tickets have been sold for each cruise.
Create an object-oriented solution with a menu that allows a user to select one of the following options:
1. Create Cruise – This option allows a user to create a new cruise by entering all necessary details (Cruise ID, route, ticket price). If the maximum number of cruises has already been created, display an error message.
2. Search Cruise – This option allows to search a cruise by the user provided cruise ID.
3. Remove Cruise – This op…
I need to know about the use and configuration of files and folders, and their attributes in Windows Server 2019.
Southern Airline has 15 daily flights from Miami to New York. Each flight requires two pilots. Flights that do not have two pilots are canceled (passengers are transferred to other airlines). The average profit per flight is $6000. Because pilots get sick from time to time, the airline is considering a policy of keeping four *reserve pilots on standby to replace sick pilots. Such pilots would introduce an additional cost of $1800 per reserve pilot (whether they fly or not).
The pilots on each flight are distinct and the likelihood of any pilot getting sick is independent of the likelihood of any other pilot getting sick. Southern believes that the probability of any given pilot getting sick is 0.15.
A) Run a simulation of this situation with at least 1000 iterations and report the following for the present policy (no reserve pilots) and the proposed policy (four reserve pilots):
The average daily utilization of the aircraft (percentage of total flights that fly)
The…
Chapter 3 Solutions
Differential Equations: Computing and Modeling (5th Edition), Edwards, Penney & Calvis
Ch. 3.1 - In Problems 1 through 16, a homogeneous...Ch. 3.1 - Prob. 2PCh. 3.1 - Prob. 3PCh. 3.1 - Prob. 4PCh. 3.1 - Prob. 5PCh. 3.1 - Prob. 6PCh. 3.1 - Prob. 7PCh. 3.1 - Prob. 8PCh. 3.1 - Prob. 9PCh. 3.1 - Prob. 10P
Ch. 3.1 - Prob. 11PCh. 3.1 - Prob. 12PCh. 3.1 - Prob. 13PCh. 3.1 - Prob. 14PCh. 3.1 - Prob. 15PCh. 3.1 - Prob. 16PCh. 3.1 - Prob. 17PCh. 3.1 - Prob. 18PCh. 3.1 - Prob. 19PCh. 3.1 - Prob. 20PCh. 3.1 - Prob. 21PCh. 3.1 - Prob. 22PCh. 3.1 - Prob. 23PCh. 3.1 - Prob. 24PCh. 3.1 - Prob. 25PCh. 3.1 - Prob. 26PCh. 3.1 - Prob. 27PCh. 3.1 - Prob. 28PCh. 3.1 - Prob. 29PCh. 3.1 - Prob. 30PCh. 3.1 - Prob. 31PCh. 3.1 - Let y1andy2 be two solutions of...Ch. 3.1 - Prob. 33PCh. 3.1 - Prob. 34PCh. 3.1 - Prob. 35PCh. 3.1 - Prob. 36PCh. 3.1 - Prob. 37PCh. 3.1 - Prob. 38PCh. 3.1 - Prob. 39PCh. 3.1 - Prob. 40PCh. 3.1 - Prob. 41PCh. 3.1 - Prob. 42PCh. 3.1 - Prob. 43PCh. 3.1 - Prob. 44PCh. 3.1 - Prob. 45PCh. 3.1 - Prob. 46PCh. 3.1 - Prob. 47PCh. 3.1 - Prob. 48PCh. 3.1 - Prob. 49PCh. 3.1 - Prob. 50PCh. 3.1 - Prob. 51PCh. 3.1 - Prob. 52PCh. 3.1 - Prob. 53PCh. 3.1 - Prob. 54PCh. 3.1 - Prob. 55PCh. 3.1 - Prob. 56PCh. 3.2 - Prob. 1PCh. 3.2 - Prob. 2PCh. 3.2 - Prob. 3PCh. 3.2 - Prob. 4PCh. 3.2 - Prob. 5PCh. 3.2 - Prob. 6PCh. 3.2 - Prob. 7PCh. 3.2 - Prob. 8PCh. 3.2 - Prob. 9PCh. 3.2 - Prob. 10PCh. 3.2 - Prob. 11PCh. 3.2 - Prob. 12PCh. 3.2 - Prob. 13PCh. 3.2 - Prob. 14PCh. 3.2 - Prob. 15PCh. 3.2 - Prob. 16PCh. 3.2 - Prob. 17PCh. 3.2 - Prob. 18PCh. 3.2 - Prob. 19PCh. 3.2 - Prob. 20PCh. 3.2 - Prob. 21PCh. 3.2 - Prob. 22PCh. 3.2 - Prob. 23PCh. 3.2 - Prob. 24PCh. 3.2 - Let Ly=y+py+qy. Suppose that y1 and y2 are two...Ch. 3.2 - Prob. 26PCh. 3.2 - Prob. 27PCh. 3.2 - Prob. 28PCh. 3.2 - Prob. 29PCh. 3.2 - Prob. 30PCh. 3.2 - Prob. 31PCh. 3.2 - Prob. 32PCh. 3.2 - Prob. 33PCh. 3.2 - Assume as known that the Vandermonde determinant...Ch. 3.2 - Prob. 35PCh. 3.2 - Prob. 36PCh. 3.2 - Prob. 37PCh. 3.2 - Prob. 38PCh. 3.2 - Prob. 39PCh. 3.2 - Prob. 40PCh. 3.2 - Prob. 41PCh. 3.2 - Prob. 42PCh. 3.2 - Prob. 43PCh. 3.2 - Prob. 44PCh. 3.3 - Find the general solutions of the differential...Ch. 3.3 - Prob. 2PCh. 3.3 - Prob. 3PCh. 3.3 - Prob. 4PCh. 3.3 - Prob. 5PCh. 3.3 - Prob. 6PCh. 3.3 - Prob. 7PCh. 3.3 - Prob. 8PCh. 3.3 - Prob. 9PCh. 3.3 - Prob. 10PCh. 3.3 - Prob. 11PCh. 3.3 - Prob. 12PCh. 3.3 - Prob. 13PCh. 3.3 - Prob. 14PCh. 3.3 - Prob. 15PCh. 3.3 - Prob. 16PCh. 3.3 - Prob. 17PCh. 3.3 - Prob. 18PCh. 3.3 - Prob. 19PCh. 3.3 - Prob. 20PCh. 3.3 - Prob. 21PCh. 3.3 - Prob. 22PCh. 3.3 - Prob. 23PCh. 3.3 - Prob. 24PCh. 3.3 - Prob. 25PCh. 3.3 - Prob. 26PCh. 3.3 - Prob. 27PCh. 3.3 - Prob. 28PCh. 3.3 - Prob. 29PCh. 3.3 - Prob. 30PCh. 3.3 - Prob. 31PCh. 3.3 - Prob. 32PCh. 3.3 - Prob. 33PCh. 3.3 - Prob. 34PCh. 3.3 - Prob. 35PCh. 3.3 - Prob. 36PCh. 3.3 - Find a function y (x ) such that y(4)(x)=y(3)(x)...Ch. 3.3 - Solve the initial value problem...Ch. 3.3 - Prob. 39PCh. 3.3 - Prob. 40PCh. 3.3 - Prob. 41PCh. 3.3 - Prob. 42PCh. 3.3 - Prob. 43PCh. 3.3 - Prob. 44PCh. 3.3 - Prob. 45PCh. 3.3 - Prob. 46PCh. 3.3 - Prob. 47PCh. 3.3 - Prob. 48PCh. 3.3 - Solve the initial value problem...Ch. 3.3 - Prob. 50PCh. 3.3 - Prob. 51PCh. 3.3 - Prob. 52PCh. 3.3 - Prob. 53PCh. 3.3 - Prob. 54PCh. 3.3 - Prob. 55PCh. 3.3 - Prob. 56PCh. 3.3 - Prob. 57PCh. 3.3 - Prob. 58PCh. 3.4 - Prob. 1PCh. 3.4 - Prob. 2PCh. 3.4 - Prob. 3PCh. 3.4 - Prob. 4PCh. 3.4 - Prob. 5PCh. 3.4 - Prob. 6PCh. 3.4 - Prob. 7PCh. 3.4 - Prob. 8PCh. 3.4 - Prob. 9PCh. 3.4 - Prob. 10PCh. 3.4 - Prob. 11PCh. 3.4 - Prob. 12PCh. 3.4 - Prob. 13PCh. 3.4 - Prob. 14PCh. 3.4 - Prob. 15PCh. 3.4 - Prob. 16PCh. 3.4 - Prob. 17PCh. 3.4 - Prob. 18PCh. 3.4 - Prob. 19PCh. 3.4 - Prob. 20PCh. 3.4 - Prob. 21PCh. 3.4 - Prob. 22PCh. 3.4 - Prob. 23PCh. 3.4 - Prob. 24PCh. 3.4 - Prob. 25PCh. 3.4 - Prob. 26PCh. 3.4 - Prob. 27PCh. 3.4 - Prob. 28PCh. 3.4 - Prob. 29PCh. 3.4 - Prob. 30PCh. 3.4 - Prob. 31PCh. 3.4 - Prob. 32PCh. 3.4 - Prob. 33PCh. 3.4 - Prob. 34PCh. 3.4 - Prob. 35PCh. 3.4 - Prob. 36PCh. 3.4 - Prob. 37PCh. 3.4 - Prob. 38PCh. 3.5 - In Problems 1 through 20, find a particular...Ch. 3.5 - Prob. 2PCh. 3.5 - Prob. 3PCh. 3.5 - Prob. 4PCh. 3.5 - Prob. 5PCh. 3.5 - Prob. 6PCh. 3.5 - Prob. 7PCh. 3.5 - Prob. 8PCh. 3.5 - Prob. 9PCh. 3.5 - Prob. 10PCh. 3.5 - Prob. 11PCh. 3.5 - Prob. 12PCh. 3.5 - Prob. 13PCh. 3.5 - Prob. 14PCh. 3.5 - Prob. 15PCh. 3.5 - Prob. 16PCh. 3.5 - Prob. 17PCh. 3.5 - Prob. 18PCh. 3.5 - Prob. 19PCh. 3.5 - Prob. 20PCh. 3.5 - Prob. 21PCh. 3.5 - Prob. 22PCh. 3.5 - Prob. 23PCh. 3.5 - Prob. 24PCh. 3.5 - Prob. 25PCh. 3.5 - Prob. 26PCh. 3.5 - Prob. 27PCh. 3.5 - Prob. 28PCh. 3.5 - Prob. 29PCh. 3.5 - Prob. 30PCh. 3.5 - Prob. 31PCh. 3.5 - Prob. 32PCh. 3.5 - Prob. 33PCh. 3.5 - Prob. 34PCh. 3.5 - Prob. 35PCh. 3.5 - Prob. 36PCh. 3.5 - Prob. 37PCh. 3.5 - Prob. 38PCh. 3.5 - Prob. 39PCh. 3.5 - Prob. 40PCh. 3.5 - Prob. 41PCh. 3.5 - Prob. 42PCh. 3.5 - Prob. 43PCh. 3.5 - Prob. 44PCh. 3.5 - Prob. 45PCh. 3.5 - Prob. 46PCh. 3.5 - Prob. 47PCh. 3.5 - Prob. 48PCh. 3.5 - Prob. 49PCh. 3.5 - Prob. 50PCh. 3.5 - Prob. 51PCh. 3.5 - Prob. 52PCh. 3.5 - Prob. 53PCh. 3.5 - Prob. 54PCh. 3.5 - Prob. 55PCh. 3.5 - Prob. 56PCh. 3.5 - You can verify by substitution that yc=c1x+c2x1 is...Ch. 3.5 - Prob. 58PCh. 3.5 - Prob. 59PCh. 3.5 - Prob. 60PCh. 3.5 - Prob. 61PCh. 3.5 - Prob. 62PCh. 3.5 - Prob. 63PCh. 3.5 - Prob. 64PCh. 3.6 - Prob. 1PCh. 3.6 - Prob. 2PCh. 3.6 - Prob. 3PCh. 3.6 - Prob. 4PCh. 3.6 - Prob. 5PCh. 3.6 - Prob. 6PCh. 3.6 - Prob. 7PCh. 3.6 - Prob. 8PCh. 3.6 - Prob. 9PCh. 3.6 - Prob. 10PCh. 3.6 - Prob. 11PCh. 3.6 - Prob. 12PCh. 3.6 - Prob. 13PCh. 3.6 - Prob. 14PCh. 3.6 - Each of Problems 15 through 18 gives the...Ch. 3.6 - Prob. 16PCh. 3.6 - Prob. 17PCh. 3.6 - Prob. 18PCh. 3.6 - A mass weighing 100 lb (mass m=3.125 slugs in fps...Ch. 3.6 - Prob. 20PCh. 3.6 - Prob. 21PCh. 3.6 - Prob. 22PCh. 3.6 - Prob. 23PCh. 3.6 - A mass on a spring without damping is acted on by...Ch. 3.6 - Prob. 25PCh. 3.6 - Prob. 26PCh. 3.6 - Prob. 27PCh. 3.6 - Prob. 28PCh. 3.6 - Prob. 29PCh. 3.6 - Prob. 30PCh. 3.7 - Problems 1 through 6 deal with the RL circuit of...Ch. 3.7 - Problems 1 through 6 deal with the RL circuit of...Ch. 3.7 - Problems 1 through 6 deal with the RL circuit of...Ch. 3.7 - Problems 1 through 6 deal with the RL circuit of...Ch. 3.7 - Problems 1 through 6 deal with the RL circuit of...Ch. 3.7 - Problems 1 through 6 deal with the RL circuit of...Ch. 3.7 - Problems 7 through 10 deal with the RC circuit in...Ch. 3.7 - Problems 7 through 10 deal with the RC circuit in...Ch. 3.7 - Problems 7 through 10 deal with the RC circuit in...Ch. 3.7 - Problems 7 through 10 deal with the RC circuit in...Ch. 3.7 - In Problems 11 through 16, the parameters of an...Ch. 3.7 - In Problems 11 through 16, the parameters of an...Ch. 3.7 - In Problems 11 through 16, the parameters of an...Ch. 3.7 - In Problems 11 through 16, the parameters of an...Ch. 3.7 - In Problems 11 through 16, the parameters of an...Ch. 3.7 - In Problems 11 through 16, the parameters of an...Ch. 3.7 - In Problems 17 through 22, an RLC circuit with...Ch. 3.7 - In Problems 17 through 22, an RLC circuit with...Ch. 3.7 - In Problems 17 through 22, an RLC circuit with...Ch. 3.7 - In Problems 17 through 22, an RLC circuit with...Ch. 3.7 - In Problems 17 through 22, an RLC circuit with...Ch. 3.7 - In Problems 17 through 22, an RLC circuit with...Ch. 3.7 - Consider an LC circuit—that is, an RLC circuit...Ch. 3.7 - Prob. 24PCh. 3.7 - Prob. 25PCh. 3.8 - Prob. 1PCh. 3.8 - Prob. 2PCh. 3.8 - Prob. 3PCh. 3.8 - Prob. 4PCh. 3.8 - Prob. 5PCh. 3.8 - Prob. 6PCh. 3.8 - Prob. 7PCh. 3.8 - Prob. 8PCh. 3.8 - Prob. 9PCh. 3.8 - Prove that the eigenvalue problem...Ch. 3.8 - Prob. 11PCh. 3.8 - Prob. 12PCh. 3.8 - Prob. 13PCh. 3.8 - Prob. 14PCh. 3.8 - A uniform cantilever beam is fixed at x=0 and free...Ch. 3.8 - Suppose that a beam is fixed at its ends...Ch. 3.8 - For the simply supported beam whose deflection...Ch. 3.8 - A beam is fixed at its left end x=0 but is simply...
Additional Engineering Textbook Solutions
Find more solutions based on key concepts
ICA 8-57
A 100-watt [W] motor (60% efficient) is available to raise a load 5 meters [m] into the air. If the ta...
Thinking Like an Engineer: An Active Learning Approach (4th Edition)
Broaching machines are simpler in a basic design than most other machine tools. Why is this?
Degarmo's Materials And Processes In Manufacturing
In Exercises 55 through 60, find the value of the given function where a and b are numeric variables of type Do...
Introduction To Programming Using Visual Basic (11th Edition)
Which category of C++ reference variables always produces aliases?
Concepts Of Programming Languages
Further modify the C++ program that you already modified in Practice Program 2. Change the multiplication sign ...
Problem Solving with C++ (10th Edition)
Explain the term cursor.
Database Concepts (8th Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, computer-science and related others by exploring similar questions and additional content below.Similar questions
- Why is JAVA OOP is really difficult to study?arrow_forwardMy daughter is a Girl Scout and it is time for our cookie sales. There are 15 neighbors nearby and she plans to visit every neighbor this evening. There is a 40% likelihood that someone will be home. If someone is home, there is an 85% likelihood that person will make a purchase. If a purchase is made, the revenue generated from the sale follows the Normal distribution with mean $18 and standard deviation $5. Using @RISK, simulate our door-to-door sales using at least 1000 iterations and report the expected revenue, the maximum revenue, and the average number of purchasers. What is the probability that the revenue will be greater than $120?arrow_forwardQ4 For the network of Fig. 1.41: a- Determine re b- Find Aymid =VolVi =Vo/Vi c- Calculate Zi. d- Find Ay smid e-Determine fL, JLC, and fLE f-Determine the low cutoff frequency. g- Sketch the asymptotes of the Bode plot defined by the cutoff frequencies of part (e). h-Sketch the low-frequency response for the amplifier using the results of part (f). Ans: 28.48 2, -72.91, 2.455 KS2, -54.68, 103.4 Hz. 38.05 Hz. 235.79 Hz. 235.79 Hz. 14V 15.6ΚΩ 68kQ 0.47µF Vo 0.82 ΚΩ V₁ B-120 3.3kQ 0.47µF 10kQ 1.2k0 =20µF Z₁ Fig. 1.41 Circuit forarrow_forward
- a. [10 pts] Write a Boolean equation in sum-of-products canonical form for the truth table shown below: A B C Y 0 0 0 1 0 0 1 0 0 1 0 0 0 1 1 0 1 0 0 1 1 0 1 0 1 1 1 1 0 1 1 0 a. [10 pts] Minimize the Boolean equation you obtained in (a). b. [10 pts] Implement, using Logisim, the simplified logic circuit. Include an image of the circuit in your report.arrow_forwardUsing XML, design a simple user interface for a fictional app. Your UI should include at least three different UI components (e.g., TextView, Button, EditText). Explain the purpose of each component in your design-you need to add screenshots of your work with your name as part of the code to appear on the interface-. Screenshot is needed.arrow_forwardQ4) A thin ring of radius 5 cm is placed on plane z = 1 cm so that its center is at (0,0,1 cm). If the ring carries 50 mA along a^, find H at (0,0,a).arrow_forward
- 4. [15 pts] A logic function F of four variables a; b; c; d is described by the following K-map. Derive the fully minimized SOP logic expression form of F. cd ab 00 01 11 10 00 0 0 0 1 01 1 0 0 1 11 1 0 1 1 10 0 0 1 1arrow_forward2. [20 pts] Student A B will enjoy his picnic on sunny days that have no ants. He will also enjoy his picnic any day he sees a hummingbird, as well as on days where there are ants and ladybugs. a. Write a Boolean equation for his enjoyment (E) in terms of sun (S), ants (A), hummingbirds (H), and ladybugs (L). b. Implement in Logisim, the logic circuit of E function. Use the Circuit Analysis tool in Logisim to view the expression, include an image of the expression generated by Logisimarrow_forwardHow would I go about creating this computer database in MariaDB with sql? Create a database name "dbXXXXXX" Select the database using the "use [database name]" command. Now you are in the database. Based on the above schema from Enrolment System database, create all the tables with the last 6 digits of "123456", then the table name for table Lecturer should be "123456_Lecturer". Refer to basic SQL lecture note to create table that has primary keys and Foreign Keys. Provide the datatype of each attributes. Add a column called "Department" with datatype "VARCHAR(12)" to the table "Lecturer". Shows the metadata of the updated "Lecturer" table. (Use Describe command) Drop the "Department" column from the table "Lecturer", and show the metadata of the updated "Lecturer" table. Insert three (3) data to each of the table in the tables created. Note: If you have foreign key issues, please disable foreign key constraints before inserting the data, see below SET FOREIGN_KEY_CHECKS=0;…arrow_forward
- CSE330 Discrete Mathematics 1. In the classes, we discussed three forms of floating number representations as given below, (1) Standard/General Form, (2) Normalized Form, (3) Denormalized Form. 3. Consider the real number x = (3.395) 10 (a) (b) Convert the decimal number x into binary format up to 7 binary places (7 binary digits after decimal) Convert the calculated value into denormalized form and calculate fl(x) for m=4 Don't use any Al tool show answer in pen a nd paper then take pi ctures and sendarrow_forwardSimplify the following expressions by means of a four-variable K-Map. AD+BD+ BC + ABDarrow_forwardCSE330 Discrete Mathematics 1. In the classes, we discussed three forms of floating number representations as given below, (1) Standard/General Form, (2) Normalized Form, (3) Denormalized Form. 2. Let ẞ 2, m = 6, emin = -3 and emax = 3. Answer the following questions: Compute the minimum of |x| for General and Normalized form (a) Compute the Machine Epsilon value for the General and Denormalized form. If we change the value of emax to 6 then how will it affect the value of maximum scale invariant error for the case of Normalized form? Explain your answer. show answer in pen a Don't use any Al tool nd paper then take pi ctures and sendarrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
C++ for Engineers and ScientistsComputer ScienceISBN:9781133187844Author:Bronson, Gary J.Publisher:Course Technology Ptr
Operations Research : Applications and AlgorithmsComputer ScienceISBN:9780534380588Author:Wayne L. WinstonPublisher:Brooks Cole
Systems ArchitectureComputer ScienceISBN:9781305080195Author:Stephen D. BurdPublisher:Cengage Learning
Principles of Information Systems (MindTap Course...Computer ScienceISBN:9781285867168Author:Ralph Stair, George ReynoldsPublisher:Cengage Learning
C++ Programming: From Problem Analysis to Program...Computer ScienceISBN:9781337102087Author:D. S. MalikPublisher:Cengage Learning
A Guide to SQLComputer ScienceISBN:9781111527273Author:Philip J. PrattPublisher:Course Technology Ptr
C++ for Engineers and Scientists
Computer Science
ISBN:9781133187844
Author:Bronson, Gary J.
Publisher:Course Technology Ptr
Operations Research : Applications and Algorithms
Computer Science
ISBN:9780534380588
Author:Wayne L. Winston
Publisher:Brooks Cole
Systems Architecture
Computer Science
ISBN:9781305080195
Author:Stephen D. Burd
Publisher:Cengage Learning
Principles of Information Systems (MindTap Course...
Computer Science
ISBN:9781285867168
Author:Ralph Stair, George Reynolds
Publisher:Cengage Learning
C++ Programming: From Problem Analysis to Program...
Computer Science
ISBN:9781337102087
Author:D. S. Malik
Publisher:Cengage Learning
A Guide to SQL
Computer Science
ISBN:9781111527273
Author:Philip J. Pratt
Publisher:Course Technology Ptr
Boolean Algebra - Digital Logic and Logic Families - Industrial Electronics; Author: Ekeeda;https://www.youtube.com/watch?v=u7XnJos-_Hs;License: Standard YouTube License, CC-BY
Boolean Algebra 1 – The Laws of Boolean Algebra; Author: Computer Science;https://www.youtube.com/watch?v=EPJf4owqwdA;License: Standard Youtube License