
A large, flat sheet carries a uniformly distributed
the sheet radiates an
(a) Find the wave function for the electric field of the wave to the right of the sheet. (b) Find the Poynting vector as a function of x and t. (c) Find the intensity of the wave. (d) What If? If the sheet is to emit
Figure P33.28
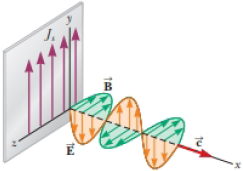
(a)
Answer to Problem 34.46P
Explanation of Solution
Given info: The wave function for the magnetic field of the wave to the right of the sheet is
Explanation:
Write the Maxwell’s third equation,
Here,
Substitute
Integrating the above equation with respect to
Substitute
The direction of electric field must be perpendicular to the direction of propagation
Conclusion:
Therefore, the wave function for the electric field of the wave to the right of the sheet is
(b)
Answer to Problem 34.46P
Explanation of Solution
Given info: The wave function for the magnetic field of the wave to the right of the sheet is
Explanation:
Write the formula to calculate the Poynting vector.
Here,
Substitute
Conclusion:
Therefore, the Poynting vector as a function of
(c)
Answer to Problem 34.46P
Explanation of Solution
Given info: The wave function for the magnetic field of the wave to the right of the sheet is
Explanation:
The wave function for the magnetic field of the wave is.
The maximum value of
The wave function for the electric field of the wave is.
The maximum value of
Write the formula to calculate the intensity of the wave is,
Here,
Substitute
Conclusion:
Therefore, the intensity of the wave is
(d)
Answer to Problem 34.46P
Explanation of Solution
Given info: The intensity of the wave is
Explanation:
The intensity of the wave from part (c) is,
Here,
Rearrange the above expression for
Substitute
Conclusion:
Therefore, the maximum value of sinusoidal current density is
Want to see more full solutions like this?
Chapter 34 Solutions
Physics for Scientists and Engineers, Technology Update (No access codes included)
- Can someone help me with this question. Thanks.arrow_forwardIdentical rays of light enter three transparent blocks composed of different materials. Light slows down upon entering the blocks.arrow_forwardFor single-slit diffraction, calculate the first three values of (the total phase difference between rays from each edge of the slit) that produce subsidiary maxima by a) using the phasor model, b) setting dr = 0, where I is given by, I = Io (sin (10) ². 2arrow_forward
 Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
 Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill
Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill





