
(a)
To draw: The sketch a graph of the electric field at the instant
(a)
Answer to Problem 46AP
The graph of the electric field is shown in the diagram below.
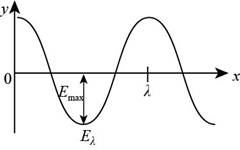
Figure (1)
Explanation of Solution
Given info: The expression for the average intensity of the wave is,
Introduction: The electric filed is a region around a charged particle within which a force would be experienced by other particles that may be attractive force or repulsive force.
The electric field in the figure is perpendicular to the magnetic field and the sinusoidal wave is travelling with the
The expression for the electric field is,
Here,
Substitute
The diagram of the electric field is shown below.
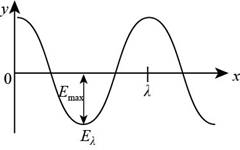
Figure (1)
(b)
The energy density
(b)
Answer to Problem 46AP
The energy density
Explanation of Solution
Given info: The expression for the average intensity of the wave is,
The formula to calculate the energy density in the electric field is,
Here,
Substitute
Thus, the energy density
Conclusion:
Therefore, the energy density
(c)
The energy density
(c)
Answer to Problem 46AP
The energy density
Explanation of Solution
Given info: The expression for the average intensity of the wave is,
The expression for the magnetic field is,
Here,
Substitute
The formula to calculate the energy density in the magnetic is,
Here,
Substitute
Thus, the energy density
Conclusion:
Therefore, the energy density
(d)
The total energy density in terms of electric field amplitude.
(d)
Answer to Problem 46AP
The total energy density in terms of electric field amplitude is
Explanation of Solution
Given info: The expression for the average intensity of the wave is,
The expression for the energy due to magnetic field at instant
The value of
Substitute
The formula to calculate the total energy density is,
Substitute
Thus, the total energy density in terms of electric field amplitude is
Conclusion:
Therefore, the total energy density in terms of electric field amplitude is
(e)
The amount of energy in the shoebox.
(e)
Answer to Problem 46AP
The amount of energy in the shoebox is
Explanation of Solution
Given info: The expression for the average intensity of the wave is,
The expression for the energy in the shoebox is,
Here,
Substitute
Integrate the above equation to find the value of
Thus, the amount of energy in the shoebox is
Conclusion:
Therefore, the amount of energy in the shoebox is
(f)
The power the wave carries through area
(f)
Answer to Problem 46AP
The power the wave carries through area
Explanation of Solution
Given info: The expression for the average intensity of the wave is,
The expression for the energy in the shoebox is,
The formula to calculate the power is,
Substitute
Thus, the power the wave carries through area
Conclusion:
Therefore, the power the wave carries through area
(g)
The intensity of the wave .
(g)
Answer to Problem 46AP
The intensity of the wave is
Explanation of Solution
Given info: The expression for the average intensity of the wave is,
The formula to calculate the intensity of the wave is,
Substitute
Thus, the intensity of the wave is
Conclusion:
Therefore, the intensity of the wave is
(h)
The comparison of the result with the equation
(h)
Answer to Problem 46AP
The expression of the result is same as that of the expression.
Explanation of Solution
Given info: The expression for the average intensity of the wave is,
The formula to calculate the average intensity is,
Substitute the average value as
Thus, the average value of the intensity is same as that given in the equation.
Conclusion:
Therefore, the expression of the result is same as that of the expression.
Want to see more full solutions like this?
Chapter 33 Solutions
Physics for Scientists and Engineers with Modern Physics
- 3) Two bumper cars of masses 600 kg and 900 kg travelling (on a smooth surface) with velocities 8m/s and 4 m/s respectively, have a head on collision. If the coefficient of restitution is 0.5. a) What sort of collision is this? b) Calculate their velocities immediately after collision. c) If the coefficient of restitution was 1 instead of 0.5, what is the amount of energy lost during collision?arrow_forwardThe rectangular loop of wire shown in the figure (Figure 1) has a mass of 0.18 g per centimeter of length and is pivoted about side ab on a frictionless axis. The current in the wire is 8.5 A in the direction shown. Find the magnitude of the magnetic field parallel to the y-axis that will cause the loop to swing up until its plane makes an angle of 30.0 ∘ with the yz-plane. Find the direction of the magnetic field parallel to the y-axis that will cause the loop to swing up until its plane makes an angle of 30.0 ∘ with the yz-plane.arrow_forwardGive a more general expression for the magnitude of the torque τ. Rewrite the answer found in Part A in terms of the magnitude of the magnetic dipole moment of the current loop m. Define the angle between the vector perpendicular to the plane of the coil and the magnetic field to be ϕ, noting that this angle is the complement of angle θ in Part A. Give your answer in terms of the magnetic moment mm, magnetic field B, and ϕ.arrow_forward
- Calculate the electric and magnetic energy densities at thesurface of a 3-mm diameter copper wire carrying a 15-A current. The resistivity ofcopper is 1.68×10-8 Ω.m.Prob. 18, page 806, Ans: uE= 5.6 10-15 J/m3 uB= 1.6 J/m3arrow_forwardA 15.8-mW laser puts out a narrow beam 2.0 mm in diameter.Suppose that the beam is in free space. What is the rms value of E in the beam? What isthe rms value of B in the beam?Prob. 28, page 834. Ans: Erms= 1380 V/m, Brms =4.59×10-6 Tarrow_forwardA 4.5 cm tall object is placed 26 cm in front of a sphericalmirror. It is desired to produce a virtual image that is upright and 3.5 cm tall.(a) What type of mirror should be used, convex, or concave?(b) Where is the image located?(c) What is the focal length of the mirror?(d) What is the radius of curvature of the mirror?Prob. 25, page 861. Ans: (a) convex, (b) di= -20.2 cm, i.e. 20.2 cm behind the mirror,(c) f= -90.55 cm, (d) r= -181.1 cm.arrow_forward
- A series RCL circuit contains an inductor with inductance L=3.32 mH, and a generator whose rms voltage is 11.2 V. At a resonant frequencyof 1.25 kHz the average power delivered to the circuit is 26.9 W.(a) Find the value of the capacitance.(b) Find the value of the resistance.(c) What is the power factor of this circuit?Ans: C=4.89 μF, R=4.66 Ω, 1.arrow_forwardA group of particles is traveling in a magnetic field of unknown magnitude and direction. You observe that a proton moving at 1.70 km/s in the +x-direction experiences a force of 2.06×10−16 N in the +y-direction, and an electron moving at 4.40 km/s in the −z-direction experiences a force of 8.10×10−16 N in the +y-direction. What is the magnitude of the magnetic force on an electron moving in the −y-direction at 3.70 km/s ? What is the direction of this the magnetic force? (in the xz-plane)arrow_forwardA particle with a charge of −5.20 nC is moving in a uniform magnetic field of B =−( 1.22 T )k^. The magnetic force on the particle is measured to be F=−( 3.50×10−7 N )i^+( 7.60×10−7 N )j^. Calculate the x component of the velocity of the particle.arrow_forward
- Is it possible for average velocity to be negative?a. Yes, in cases when the net displacement is negative.b. Yes, if the body keeps changing its direction during motion.c. No, average velocity describes only magnitude and not the direction of motion.d. No, average velocity describes only the magnitude in the positive direction of motion.arrow_forwardTutorial Exercise An air-filled spherical capacitor is constructed with an inner-shell radius of 6.95 cm and an outer-shell radius of 14.5 cm. (a) Calculate the capacitance of the device. (b) What potential difference between the spheres results in a 4.00-μC charge on the capacitor? Part 1 of 4 - Conceptualize Since the separation between the inner and outer shells is much larger than a typical electronic capacitor with separation on the order of 0.1 mm and capacitance in the microfarad range, we expect the capacitance of this spherical configuration to be on the order of picofarads. The potential difference should be sufficiently low to avoid sparking through the air that separates the shells. Part 2 of 4 - Categorize We will calculate the capacitance from the equation for a spherical shell capacitor. We will then calculate the voltage found from Q = CAV.arrow_forwardI need help figuring out how to do part 2 with the information given in part 1 and putting it in to the simulation. ( trying to match the velocity graph from the paper onto the simulation to find the applied force graph) Using this simulation https://phet.colorado.edu/sims/cheerpj/forces-1d/latest/forces-1d.html?simulation=forces-1d.arrow_forward
 Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
 Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill
Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill





