Chapter 3.3, Problem

(a)

To determine

To find the median, first and third quartiles of the Giants’ salaries.

Answer

Median $=1.30$, First quartile = $0.48$ and third quartile = $5.075$

Explanation of Solution

Given:

The data for Giants’ salaries is given by

19.00	18.25	16.17	10.00	8.50
6.00	6.00	5.00	4.85	4.25
3.20	3.00	2.20	1.58	1.30
1.25	1.00	0.75	0.63	0.62
0.56	0.48	0.48	0.48	0.48
0.48	0.48	0.48	0.48

Formula used:

First quartile $Q_1=\frac{1}{4}{(n+1)}^{th}value$

If $\frac{1}{4}(n+1)$ is not an integer, then

$Q_1=x_{\mathrm{int}eger\left(\frac{1}{4}(n+1)\right)}+\left(x_{\mathrm{int}eger\left(\frac{1}{4}(n+1)\right)+1}-x_{\mathrm{int}eger\left(\frac{1}{4}(n+1)\right)}\right)\left(decimal\left(\left(\frac{1}{4}(n+1)\right)\right)\right)$

Third quartile $Q_3=\frac{3}{4}{(n+1)}^{th}value$

If $\frac{3}{4}(n+1)$ is not an integer, then

$Q_1=x_{\mathrm{int}eger\left(\frac{3}{4}(n+1)\right)}+\left(x_{\mathrm{int}eger\left(\frac{3}{4}(n+1)\right)+1}-x_{\mathrm{int}eger\left(\frac{3}{4}(n+1)\right)}\right)\left(decimal\left(\left(\frac{3}{4}(n+1)\right)\right)\right)$

Median is given by

$\begin{array}{c}\text{Median}={\left(\frac{n+1}{2}\right)}^{th}\text{value}\text{for}\text{odd}n\\ =\frac{1}{2}\left[{\left(\frac{n}{2}\right)}^{th}\text{value}+{\left(\frac{n}{2}+1\right)}^{th}\text{value}\right]\text{for}\text{even}n\end{array}$

Calculation:

Given data sorted in ascending order:

x
0.48
0.48
0.48
0.48
0.48
0.48
0.48
0.48
0.56
0.62
0.63
0.75
1.00
1.25
1.30
1.58
2.20
3.00
3.20
4.25
4.85
5.00
6.00
6.00
8.50
10.00
16.17
18.25
19.00

Here, n = 29

First need to find First quartile and third quartile

First Quartile:

$\begin{array}{c}$ Q_1=\frac{1}{4}{(29+1)}^{th}\text{value}$$ =\frac{1}{4}{(30)}^{th}\text{value}$$ ={(7.5)}^{th}\text{value}$=0.48+0.5\times \left(0.48-0.48\right)\\ =0.48\end{array}$

First quartile is $0.48$.

Third quartile:

$\begin{array}{c}$ Q_3=\frac{3}{4}{(n+1)}^{th}\text{value}$$ =\frac{3}{4}{(29+1)}^{th}\text{value}$$ =\frac{3}{4}{(30)}^{th}\text{value}$$ ={(22.5)}^{th}\text{value}$=5.00+0.5\left(5.00-4.85\right)\\ =5.00+0.5\times 0.15\\ =5.00+0.075\\ =5.075\end{array}$

Third quartile is $5.15$.

Here $n=29$, which is odd

$\begin{array}{c}\text{Median}={\left(\frac{29+1}{2}\right)}^{th}\text{value}\\ ={15}^{th}\text{value}\\ \text{=1}\text{.30}\end{array}$

(b)

To determine

To find the median, first and third quartiles of the Tigers’ salaries.

Answer

Median $=1.10$, First quartile = $0.49$ and third quartile = $5.50$

Explanation of Solution

Given:

The data for Tigers’ salaries is given by

23.00	21.00	20.10	13.00	9.00
6.73	5.50	5.50	5.50	3.75
3.10	2.10	2.10	2.10	1.10
1.00	0.90	0.51	0.51	0.50
0.50	0.50	0.49	0.49	0.49
0.48	0.48	0.48	0.48

Formula used:

First quartile $Q_1=\frac{1}{4}{(n+1)}^{th}value$

If $\frac{1}{4}(n+1)$ is not an integer, then

$Q_1=x_{\mathrm{int}eger\left(\frac{1}{4}(n+1)\right)}+\left(x_{\mathrm{int}eger\left(\frac{1}{4}(n+1)\right)+1}-x_{\mathrm{int}eger\left(\frac{1}{4}(n+1)\right)}\right)\left(decimal\left(\left(\frac{1}{4}(n+1)\right)\right)\right)$

Third quartile $Q_3=\frac{3}{4}{(n+1)}^{th}value$

If $\frac{3}{4}(n+1)$ is not an integer, then

$Q_1=x_{\mathrm{int}eger\left(\frac{3}{4}(n+1)\right)}+\left(x_{\mathrm{int}eger\left(\frac{3}{4}(n+1)\right)+1}-x_{\mathrm{int}eger\left(\frac{3}{4}(n+1)\right)}\right)\left(decimal\left(\left(\frac{3}{4}(n+1)\right)\right)\right)$

Median is given by

$\begin{array}{c}\text{Median}={\left(\frac{n+1}{2}\right)}^{th}\text{value}\text{for}\text{odd}n\\ =\frac{1}{2}\left[{\left(\frac{n}{2}\right)}^{th}\text{value}+{\left(\frac{n}{2}+1\right)}^{th}\text{value}\right]\text{for}\text{even}n\end{array}$

Calculation:

Given data sorted in ascending order:

x
0.48
0.48
0.48
0.48
0.49
0.49
0.49
0.50
0.50
0.50
0.51
0.51
0.90
1.00
1.10
2.10
2.10
3.00
3.10
3.75
5.50
5.50
5.50
6.73
9.00
13.00
20.10
21.0
23.00

Here, n = 29

First need to find First quartile and third quartile

First Quartile:

$\begin{array}{c}$ Q_1=\frac{1}{4}{(29+1)}^{th}\text{value}$$ =\frac{1}{4}{(30)}^{th}\text{value}$$ ={(7.5)}^{th}\text{value}$=0.49+0.5\times \left(0.49-0.49\right)\\ =0.49\end{array}$

First quartile is $0.49$.

Third quartile:

$\begin{array}{c}$ Q_3=\frac{3}{4}{(n+1)}^{th}\text{value}$$ =\frac{3}{4}{(29+1)}^{th}\text{value}$$ =\frac{3}{4}{(30)}^{th}\text{value}$$ ={(22.5)}^{th}\text{value}$=5.50+0.5\left(5.50-5.50\right)\\ =5.50\end{array}$

Third quartile is $5.50$.

Here $n=29$, which is odd

$\begin{array}{c}\text{Median}={\left(\frac{29+1}{2}\right)}^{th}\text{value}\\ ={15}^{th}\text{value}\\ \text{=1}\text{.10}\end{array}$

(c)

To determine

To find upper and lower outlier boundaries of Giants’ salaries.

Answer

Lower outlier boundary of Giants’ salaries. is $-6.415$.

Upper outlier boundary of Giants’ salaries. is $11.9675$.

Explanation of Solution

Given:

From part (a)

$\begin{array}{l}{Q}_1=0.48\\ Q_3=5.075\end{array}$

Formula used:

IQR: Inter Quartile Range

$IQR=Q_3-Q_1$

Calculation:

$\begin{array}{c}IQR=Q_3-Q_1\\ =5.075-0.48\\ =4.595\end{array}$

Therefore,

$\begin{array}{c}\text{Lower outlier limit }=\left(Q_1\right)-1.5\times IQR\\ =0.48-1.5\times 4.595\\ =0.48-6.895\\ =-6.415\\ \text{Upper outlier limit }=\left(Q_3\right)+1.5\times IQR\\ =5.075+1.5\times 4.595\\ =5.075+6.895\\ =11.9675\end{array}$

d)

To determine

To find upper and lower outlier boundaries of Tigers’ salaries.

Answer

Lower outlier boundary of Tigers’ salaries. is $-7.025$.

Upper outlier boundary of Tigers’ salaries. is $13.015$.

Explanation of Solution

Given:

From part (b)

$\begin{array}{l}{Q}_1=0.49\\ Q_3=5.50\end{array}$

Formula used:

IQR: Inter Quartile Range

$IQR=Q_3-Q_1$

Calculation:

$\begin{array}{c}IQR=Q_3-Q_1\\ =5.50-0.49\\ =5.01\end{array}$

Therefore,

$\begin{array}{c}\text{Lower outlier limit }=\left(Q_1\right)-1.5\times IQR\\ =0.49-1.5\times 5.01\\ =0.49-7.515\\ =-7.025\\ \text{Upper outlier limit }=\left(Q_3\right)+1.5\times IQR\\ =5.5+1.5\times 5.01\\ =5.5+7.515\\ =13.015\end{array}$

(e)

To determine

To construct a boxplot for Tigers’ salaries and Giants’ salaries and compare.

Explanation of Solution

Boxplot from given datafor Tigers’ salaries and Giants’ salaries are constructed below.

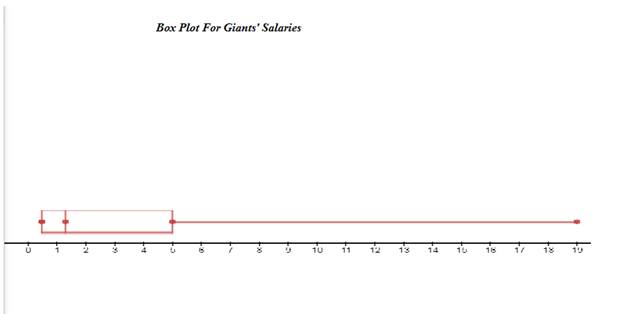
From the above box plot, it can be concluded that 19 is the outlier value which is greater than upper outlier limit.

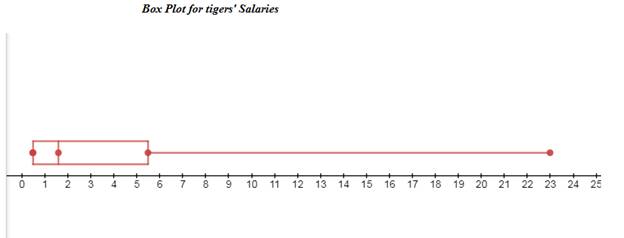
From the above box plot, it can be concluded that 23 is the outlier value which is greater than upper outlier limit.