
Concept explainers
(a)
To find the first and third
(a)
Answer to Problem 32E
First quartile = 1414.75 and third quartile = 2931
Explanation of Solution
Formula used:
First quartile
If
Third quartile
If
Calculation:
Data sorted in ascending order:
| |
|||||
| 135 | 1229 | 1658 | 2128 | 2486 | 3843 |
| 559 | 1339 | 1686 | 2155 | 2561 | 3968 |
| 700 | 1359 | 1704 | 2166 | 2831 | 4055 |
| 984 | 1366 | 1730 | 2218 | 2915 | 4392 |
| 1090 | 1431 | 1803 | 2273 | 2979 | 4472 |
| 1127 | 1433 | 1808 | 2320 | 3329 | 4809 |
| 1128 | 1507 | 1880 | 2321 | 3336 | 5434 |
| 1176 | 1526 | 2015 | 2395 | 3375 | 8460 |
| 1177 | 1592 | 2071 | 2427 | 3637 | |
| 1211 | 1598 | 2096 | 2459 | 3672 | |
Here, n = 58
First need to find First quartile and third quartile
First Quartile:
First quartile is 1414.75
Third quartile:
Third quartile is 2931.
(b)
To find
(b)
Answer to Problem 32E
Median is 2083.5
Explanation of Solution
Formula used:
Calculation:
Here
(c)
To find upper and lower outlier boundaries.
(c)
Answer to Problem 32E
Lower outlier boundary is -859.625
Upper outlier boundary is 5205.375
Explanation of Solution
Given:
From part (a)
Formula used:
IQR:
Calculation:
Therefore,
And
d)
To find the 135 and 559 are outliers or not.
d)
Answer to Problem 32E
135 and 559 are not outliers.
Explanation of Solution
Outliers are those values which are less than
Here,
Lower outlier boundary is -859.625
Upper outlier boundary is 5205.375
135 and 559 are within
(e)
To find the 8460 and 5434 are outliers or not.
(e)
Answer to Problem 32E
The 8460 and 5434 are outliers.
Explanation of Solution
Outliers are those values which are less than
Here,
Lower outlier boundary is -859.625
Upper outlier boundary is 5205.375
8460 and 5434 are greater than upper outlier limit 5205.375. Hence both are outliers.
(f)
To construct a boxplot from given data.
(f)
Explanation of Solution
Boxplot from given data:
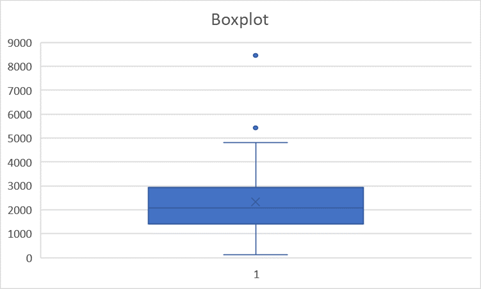
(g)
To find shape of the distribution.
(g)
Answer to Problem 32E
The shape of the distribution is Positively skewed.
Explanation of Solution
Since the difference between the median and third quartile is larger than the difference between first quartile and median. Which also means that median is close to first quartile therefore the shape of distribution is right skewed or positively skewed.
(h)
To find 15s t percentile.
(h)
Answer to Problem 32E
15s t percentile is 1176.85
Explanation of Solution
Calculation:
Therefore, the percentile can be calculated as
(i)
To find 65t h percentile.
(i)
Answer to Problem 32E
65t h percentile is 2406.2
Explanation of Solution
Calculation:
Therefore,
(j)
To find percentile rank for 1433 words.
(j)
Answer to Problem 32E
Percentile rank for 1433 words is 25.86%.
Explanation of Solution
Formula used:
Calculation:
Number of values below 1433 is 15.
Want to see more full solutions like this?
Chapter 3 Solutions
Elementary Statistics (Text Only)
- Business Discussarrow_forwardThe following data represent total ventilation measured in liters of air per minute per square meter of body area for two independent (and randomly chosen) samples. Analyze these data using the appropriate non-parametric hypothesis testarrow_forwardeach column represents before & after measurements on the same individual. Analyze with the appropriate non-parametric hypothesis test for a paired design.arrow_forward
- Should you be confident in applying your regression equation to estimate the heart rate of a python at 35°C? Why or why not?arrow_forwardGiven your fitted regression line, what would be the residual for snake #5 (10 C)?arrow_forwardCalculate the 95% confidence interval around your estimate of r using Fisher’s z-transformation. In your final answer, make sure to back-transform to the original units.arrow_forward
 Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt
Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt



