Chapter 3.2, Problem 34E

Beer: The following table presents the number of active breweries for samples of states located east and west of the Mississippi River.

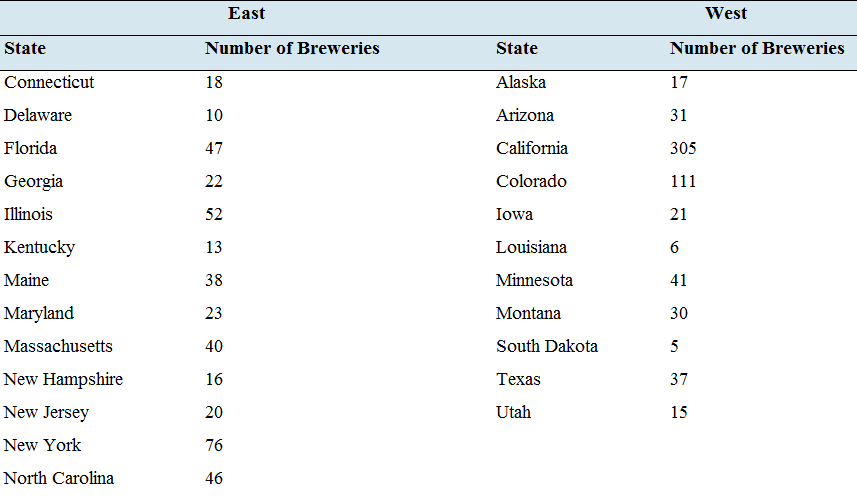
1. Compute the sample standard deviation for the number of breweries east of the Mississippi River.
2. Compute the sample standard deviation for the number of breweries west of the Mississippi River.
3. Compute the range for each data set.
4. Based on the standard deviations, which region has the greater spread in the number of breweries?
5. Based on the ranges, which region has the greater spread in the number of breweries?
6. The sample of western states happens to include California. Remove California from the sample of western states, and compute the sample standard deviation for the remaining western states. Does the result show that the standard deviation is not resistant? Explain.
7. Compute the range for the western states with California removed. Is the range resistant? Explain.

To determine

To find: the sample standard deviation of no. of breweries of east of river Mississippi.

Answer to Problem 34E

Standard deviation = 18.30

Explanation of Solution

Given:

East		West
State	Number of Breweries	State	Number of Breweries
Connecticut	18	Alaska	17
Delaware	10	Arizona	31
Florida	47	California	305
Georgia	22	Colorado	111
Illinois	52	Iowa	21
Kentucky	13	Louisiana	6
Maine	38	Minnesota	41
Maryland	23	Montana	30
Massachusetts	40	South Dakota	5
New Hampshire	16	Texas	37
New Jersey	20	Utah	15
New York	76
North Carolina	46
South Carolina	14
Tennessee	19
Vermont	20

Formula used:

  $\text{Standard}\text{Deviation = }\sqrt{\frac{\sum {\left(x_i-\overline{x}\right)}^2}{n-1}}$

Calculation:

East(x)
State	Number of Breweries	${\left(x_i-\overline{x}\right)}^2$
Connecticut	18	135.14
Delaware	10	385.14
Florida	47	301.89
Georgia	22	58.14
Illinois	52	500.64
Kentucky	13	276.39
Maine	38	70.14
Maryland	23	43.89
Massachusetts	40	107.64
New Hampshire	16	185.64
New Jersey	20	92.64
New York	76	2150.64
North Carolina	46	268.14
South Carolina	14	244.14
Tennessee	19	112.89
Vermont	20	92.64
Sum	474	5025.75
Mean	29.625
Standard deviation	18.30

  $\begin{array}{c}\text{Standard}\text{Deviation = }\sqrt{\frac{5027.75}{15}}\\ =18.30\end{array}$

To determine

To find: the sample standard deviation of no. of breweries of west of river Mississippi.

Answer to Problem 34E

Standard deviation = 18.30

Explanation of Solution

Calculation:

West(y)
State	Number of Breweries	${\left(y_i-\overline{y}\right)}^2$
Alaska	17	1542.35
Arizona	31	638.71
California	305	61865.26
Colorado	111	2995.07
Iowa	21	1244.17
Louisiana	6	2527.35
Minnesota	41	233.26
Montana	30	690.26
South Dakota	5	2628.89
Texas	37	371.44
Utah	15	1703.44
Sum	619	76440.18182
Mean	56.27
Standard deviation	87.43

  $\begin{array}{c}\text{Standard}\text{Deviation = }\sqrt{\frac{76440.18182}{10}}\\ =87.43\end{array}$

To determine

To find: the range for both data set.

Answer to Problem 34E

East = 66

West =300

Explanation of Solution

Formula used:

  $\text{Range = Highest Value - Lowest Value}$

Calculation:

  $\begin{array}{c}{\text{Range}}_{\left(\text{East}\right)}=76-10\\ =66\end{array}$

  $\begin{array}{c}{\text{Range}}_{\left(\text{West}\right)}=305-5\\ =300\end{array}$

To determine

To explain based on standard deviation which region is having more spread.

Answer to Problem 34E

West is widely spread as compared to the East.

Explanation of Solution

Since the standard deviation of East is 18.30 and for west it is 87.43, which shows that there is very high standard deviation in west.

Therefore, west is having higher spread.

To determine

To explain: based on range which region is having more spread.

Answer to Problem 34E

West is widely spread as compared to the East.

Explanation of Solution

Since the Range of East is 66 and for west it is 300, which shows that there is very high Range in west.

Therefore, west is having higher spread.

To determine

To find: the sample standard deviation of no. of breweries of west of river Mississippi. After removing the California.

Answer to Problem 34E

Standard deviation = 18.30

Explanation of Solution

Calculation:

West(y)
State	Number of Breweries	${\left(y_i-\overline{y}\right)}^2$
Alaska	17	207.36
Arizona	31	0.16
Colorado	111	6336.16
Iowa	21	108.16
Louisiana	6	645.16
Minnesota	41	92.16
Montana	30	1.96
South Dakota	5	696.96
Texas	37	31.36
Utah	15	268.96
Sum	314	8388.4
Mean	31.40
Standard deviation	30.53

  $\begin{array}{c}\text{Standard}\text{Deviation = }\sqrt{\frac{8388.4}{9}}\\ =30.53\end{array}$

Yes, the standard deviation West has decreased a lot, which shows that the standard deviation is not resistant at all.

To determine

To find the sample standard deviation of no. of breweries of west of river Mississippi. After removing the California.

Answer to Problem 34E

Range = 106

Explanation of Solution

Calculation:

West(y)
State	Number of Breweries	${\left(y_i-\overline{y}\right)}^2$
Alaska	17	207.36
Arizona	31	0.16
Colorado	111	6336.16
Iowa	21	108.16
Louisiana	6	645.16
Minnesota	41	92.16
Montana	30	1.96
South Dakota	5	696.96
Texas	37	31.36
Utah	15	268.96
Sum	314	8388.4
Mean	31.40
Standard deviation	30.53

  $\begin{array}{c}\text{Range = 111 - 5}\\ \text{=106}\end{array}$

Yes, the Range West has decreased a lot, which shows that Range is not resistant at all.

The new range is 106.