
Concept explainers
a.
To graph:
The given function using a graphing utility.
a.
Answer to Problem 99E
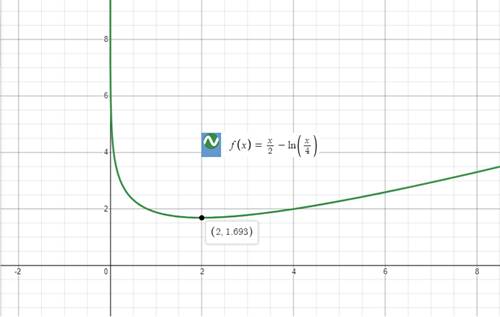
The graph of our given function would be:
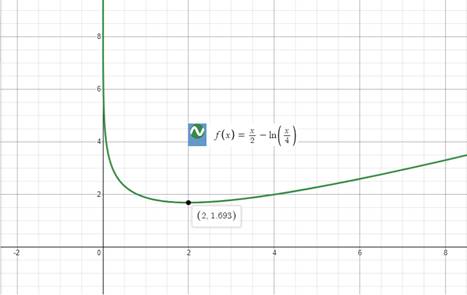
Explanation of Solution
Given:
A function:
Calculation:
Upon graphing the given functionusing a graphing utility, we will get our required graph as shown below:
b.
To find:
The domain of the given function.
b.
Answer to Problem 99E
The domain of our given logarithmic function would be
Explanation of Solution
Given:
A function:
Calculation:
We know that logarithmic functions are not defined for negative values. To find domain of our given function, we will set argument of log function greater than 0 as:
Therefore, the domain of our given logarithmic function would be
c.
To find:
Open intervals on which the given function is increasing and decreasing using the graph of function.
c.
Answer to Problem 99E
The function is decreasing on interval
Explanation of Solution
Given:
A function:
Calculation:
Upon looking at graph of our given function, we can see that function is decreasing from 0 to 2 and increasing from 2 to positive infinity.
Therefore, the function is decreasing on interval
d.
To approximate:
The
d.
Answer to Problem 99E
The relative minimum of the given function is
Explanation of Solution
Given:
A function:
Calculation:
We can see from our given graph that there is no maximum value for our given function.
We can see that the minimum value of our given function occurs at
Therefore, the relative minimum of the given function is
Chapter 3 Solutions
EP PRECALC.GRAPHING APPR.-WEBASSIGN-1YR
- For each given function f(x) find f'(x) using the rules learned in section 9.5. 1. f(x)=x32 32x 2. f(x)=7x+13 3. f(x) = x4 4. f(x) = √√x³ 5. f(x) = 3x²+ 3 x2arrow_forwardFind: lim x →-6 f (x) limx-4 f (x) lim x-1 f (x) lim x →4 f (x) (-6,3) • (-1,5) -8 -7 (-6,-2) 4+ (4,5) (4,2) • (-1,1) -6arrow_forward3 2 Find: ƒ(1) lim f(x) 14-x 2 ƒ(2) lim f(x) x-2- lim f(x) x+2+ lim f(x) x→4 3 y=f(x)arrow_forward
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





