EP PRECALC.GRAPHING APPR.-WEBASSIGN-1YR

8th Edition

ISBN: 9780357022078

Author: Larson

Publisher: CENGAGE L

See similar textbooks

Videos

Question

Chapter 3.2, Problem 114E

(a).

To determine

Tograph : the given function and approximate the required rate of ventilation in a room with 300 cubic feet of air space per child.

(a).

Expert Solution

Explanation of Solution

Given information :

The model:

y=80.4−11lnx,100≤x≤1500

The model approximates the minimum required rate of ventilation y (in cubic feet per minute per child) in a classroom with x cubic feet of air space per child.

The cubic feet of air space per child, x=300

Graph :

As per the problem,

For the function, y=80.4−11lnx,

Sketch the graph using graphing utility.

Step 1: Press WINDOW button to access the Window editor.

Step 2: Press Y= button.

Step 3: Enter the expression, y=80.4−11lnx , which is required to graph.

Step 4: Press GRAPH button to graph the functions.

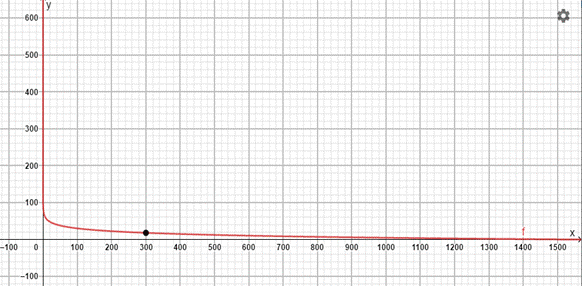
EP PRECALC.GRAPHING APPR.-WEBASSIGN-1YR, Chapter 3.2, Problem 114E , additional homework tip 1

Interpretation:From the graph,

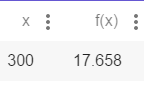
EP PRECALC.GRAPHING APPR.-WEBASSIGN-1YR, Chapter 3.2, Problem 114E , additional homework tip 2

Therefore, for 300 cubic feet of air space per child, the required rate of ventilation in a room is 17.658 cubic feet per minute per child.

(b).

To determine

Tocalculate : the rate of ventilation per child.

(b).

Expert Solution

Answer to Problem 114E

The rate of ventilation is 15 cubic feet per minute per child.

Explanation of Solution

Given information :

The model:

y=80.4−11lnx,100≤x≤1500

The model approximates the minimum required rate of ventilation y (in cubic feet per minute per child) in a classroom with x cubic feet of air space per child.

Total number of students in the classroom is 30

The total cubic feet of air per minute is 450

Calculation :

As per the problem,

Total number of students in the classroom is 30

The total cubic feet of air per minute is 450

The rate of ventilation y is the cubic feet of air per minute per child.

Therefore,

y=total cubic feet of air per minutetotal number students =45030 =15 cubic feet of air per minute per child .

(c).

To determine

Toestimate : the minimum required air space per child for the classroom in part(b), using the graph obtained in part(a).

(c).

Expert Solution

Answer to Problem 114E

382 cubic feet of air space per childis the minimum required air space per child for the classroom having 15 cubic feet per minute per child.

Explanation of Solution

Given information :

Consider the graph obtained in part (a).

The rate of ventilation per child, y=15 cubic feet per minute per child.

As per the problem,

Consider the graph obtained in part (a):

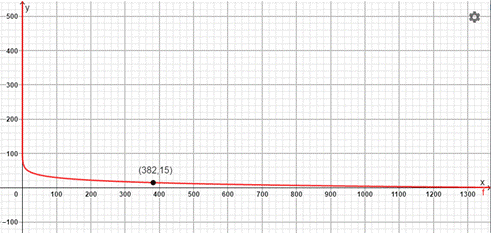
EP PRECALC.GRAPHING APPR.-WEBASSIGN-1YR, Chapter 3.2, Problem 114E , additional homework tip 3

From the graph, for y=15 , x=382

Therefore, the minimum required air space per child for the classroom, having 15 cubic feet per minute per child, is 382 cubic feet of air space per child.

(d).

To determine

Toexplain : the rate of ventilation is adequate for the classroom in part (b) having the given volume.

(d).

Expert Solution

Answer to Problem 114E

The rate of ventilation for the classroom, 15 cubic feet per minute per child, is adequate, as the minimum required rate of ventilation for the classroom is 14.9 cubic feet per minute per child.

Explanation of Solution

Given information :

The classroom of 30 students has 960 square feet of floor space and a ceiling that is 12 feet high.

Therate of ventilation for the classroom having 30 students is 15 cubic feet per minute per child (calculated in part (b)).

The model:

y=80.4−11lnx,100≤x≤1500

The model approximates the minimum required rate of ventilation y (in cubic feet per minute per child) in a classroom with x cubic feet of air space per child.

As per the problem,

Total students in the classroom is 30

The floor space of the classroom is 960 square feet.

The height of the ceiling of the classroom is 12 feet.

Therefore, volume of the classroom or the total cubic feet of air spaceis

=(960 square feet)(12 feet)=11,520 cubic feet

The cubic feet of air space per child is

x=total cubic feet of air spacetotal number students =1152030x=384 cubic feet of air per child

Substitute x=384 in the model to find the rate of ventilation, y .

y=80.4−11ln(384)y≈14.9

Therefore, the minimum required rate of ventilation for the classroom is 14.9 cubic feet per minute per child.

Thus, the rate of ventilation for the classroom, 15 cubic feet per minute per child, is adequate.

Chapter 3.2, Problem 113E

Chapter 3.2, Problem 115E

Chapter 3 Solutions

EP PRECALC.GRAPHING APPR.-WEBASSIGN-1YR

Ch. 3.1 - Prob. 1E Ch. 3.1 - Prob. 2E Ch. 3.1 - Prob. 3E Ch. 3.1 - Prob. 4E Ch. 3.1 - Prob. 5E Ch. 3.1 - Prob. 6E Ch. 3.1 - Prob. 7E Ch. 3.1 - Prob. 8E Ch. 3.1 - Prob. 9E Ch. 3.1 - Prob. 10E

Ch. 3.1 - Prob. 11E Ch. 3.1 - Prob. 12E Ch. 3.1 - Prob. 13E Ch. 3.1 - Prob. 14E Ch. 3.1 - Prob. 15E Ch. 3.1 - Prob. 16E Ch. 3.1 - Prob. 17E Ch. 3.1 - Prob. 18E Ch. 3.1 - Prob. 19E Ch. 3.1 - Prob. 20E Ch. 3.1 - Prob. 21E Ch. 3.1 - Prob. 22E Ch. 3.1 - Prob. 23E Ch. 3.1 - Prob. 24E Ch. 3.1 - Prob. 25E Ch. 3.1 - Prob. 26E Ch. 3.1 - Prob. 27E Ch. 3.1 - Prob. 28E Ch. 3.1 - Prob. 29E Ch. 3.1 - Prob. 30E Ch. 3.1 - Prob. 31E Ch. 3.1 - Prob. 32E Ch. 3.1 - Prob. 33E Ch. 3.1 - Prob. 34E Ch. 3.1 - Prob. 35E Ch. 3.1 - Prob. 36E Ch. 3.1 - Prob. 37E Ch. 3.1 - Prob. 38E Ch. 3.1 - Prob. 39E Ch. 3.1 - Prob. 40E Ch. 3.1 - Prob. 41E Ch. 3.1 - Prob. 42E Ch. 3.1 - Prob. 43E Ch. 3.1 - Prob. 44E Ch. 3.1 - Prob. 45E Ch. 3.1 - Prob. 46E Ch. 3.1 - Prob. 47E Ch. 3.1 - Prob. 48E Ch. 3.1 - Prob. 49E Ch. 3.1 - Prob. 50E Ch. 3.1 - Prob. 51E Ch. 3.1 - Prob. 52E Ch. 3.1 - Prob. 53E Ch. 3.1 - Prob. 54E Ch. 3.1 - Prob. 55E Ch. 3.1 - Prob. 56E Ch. 3.1 - Prob. 57E Ch. 3.1 - Prob. 58E Ch. 3.1 - Prob. 59E Ch. 3.1 - Prob. 60E Ch. 3.1 - Prob. 61E Ch. 3.1 - Prob. 62E Ch. 3.1 - Prob. 63E Ch. 3.1 - Prob. 64E Ch. 3.1 - Prob. 65E Ch. 3.1 - Prob. 66E Ch. 3.1 - Prob. 67E Ch. 3.1 - Prob. 68E Ch. 3.1 - Prob. 69E Ch. 3.1 - Prob. 70E Ch. 3.1 - Prob. 71E Ch. 3.1 - Prob. 72E Ch. 3.1 - Prob. 73E Ch. 3.1 - Prob. 74E Ch. 3.1 - Prob. 75E Ch. 3.1 - Prob. 76E Ch. 3.1 - Prob. 77E Ch. 3.1 - Prob. 78E Ch. 3.1 - Prob. 79E Ch. 3.1 - Prob. 80E Ch. 3.1 - Prob. 81E Ch. 3.1 - Prob. 82E Ch. 3.1 - Prob. 83E Ch. 3.1 - Prob. 84E Ch. 3.1 - Prob. 85E Ch. 3.1 - Prob. 86E Ch. 3.1 - Prob. 87E Ch. 3.1 - Prob. 88E Ch. 3.1 - Prob. 89E Ch. 3.1 - Prob. 90E Ch. 3.1 - Prob. 91E Ch. 3.1 - Prob. 92E Ch. 3.1 - Prob. 93E Ch. 3.2 - Prob. 1E Ch. 3.2 - Prob. 2E Ch. 3.2 - Prob. 3E Ch. 3.2 - Prob. 4E Ch. 3.2 - Prob. 5E Ch. 3.2 - Prob. 6E Ch. 3.2 - Prob. 7E Ch. 3.2 - Prob. 8E Ch. 3.2 - Prob. 9E Ch. 3.2 - Prob. 10E Ch. 3.2 - Prob. 11E Ch. 3.2 - Prob. 12E Ch. 3.2 - Prob. 13E Ch. 3.2 - Prob. 14E Ch. 3.2 - Prob. 15E Ch. 3.2 - Prob. 16E Ch. 3.2 - Prob. 17E Ch. 3.2 - Prob. 18E Ch. 3.2 - Prob. 19E Ch. 3.2 - Prob. 20E Ch. 3.2 - Prob. 21E Ch. 3.2 - Prob. 22E Ch. 3.2 - Prob. 23E Ch. 3.2 - Prob. 24E Ch. 3.2 - Prob. 25E Ch. 3.2 - Prob. 26E Ch. 3.2 - Prob. 27E Ch. 3.2 - Prob. 28E Ch. 3.2 - Prob. 29E Ch. 3.2 - Prob. 30E Ch. 3.2 - Prob. 31E Ch. 3.2 - Prob. 32E Ch. 3.2 - Prob. 33E Ch. 3.2 - Prob. 34E Ch. 3.2 - Prob. 35E Ch. 3.2 - Prob. 36E Ch. 3.2 - Prob. 37E Ch. 3.2 - Prob. 38E Ch. 3.2 - Prob. 39E Ch. 3.2 - Prob. 40E Ch. 3.2 - Prob. 41E Ch. 3.2 - Prob. 42E Ch. 3.2 - Prob. 43E Ch. 3.2 - Prob. 44E Ch. 3.2 - Prob. 45E Ch. 3.2 - Prob. 46E Ch. 3.2 - Prob. 47E Ch. 3.2 - Prob. 48E Ch. 3.2 - Prob. 49E Ch. 3.2 - Prob. 50E Ch. 3.2 - Prob. 51E Ch. 3.2 - Prob. 52E Ch. 3.2 - Prob. 53E Ch. 3.2 - Prob. 54E Ch. 3.2 - Prob. 55E Ch. 3.2 - Prob. 56E Ch. 3.2 - Prob. 57E Ch. 3.2 - Prob. 58E Ch. 3.2 - Prob. 59E Ch. 3.2 - Prob. 60E Ch. 3.2 - Prob. 61E Ch. 3.2 - Prob. 62E Ch. 3.2 - Prob. 63E Ch. 3.2 - Prob. 64E Ch. 3.2 - Prob. 65E Ch. 3.2 - Prob. 66E Ch. 3.2 - Prob. 67E Ch. 3.2 - Prob. 68E Ch. 3.2 - Prob. 69E Ch. 3.2 - Prob. 70E Ch. 3.2 - Prob. 71E Ch. 3.2 - Prob. 72E Ch. 3.2 - Prob. 73E Ch. 3.2 - Prob. 74E Ch. 3.2 - Prob. 75E Ch. 3.2 - Prob. 76E Ch. 3.2 - Prob. 77E Ch. 3.2 - Prob. 78E Ch. 3.2 - Prob. 79E Ch. 3.2 - Prob. 80E Ch. 3.2 - Prob. 81E Ch. 3.2 - Prob. 82E Ch. 3.2 - Prob. 83E Ch. 3.2 - Prob. 84E Ch. 3.2 - Prob. 85E Ch. 3.2 - Prob. 86E Ch. 3.2 - Prob. 87E Ch. 3.2 - Prob. 88E Ch. 3.2 - Prob. 89E Ch. 3.2 - Prob. 90E Ch. 3.2 - Prob. 91E Ch. 3.2 - Prob. 92E Ch. 3.2 - Prob. 93E Ch. 3.2 - Prob. 94E Ch. 3.2 - Prob. 95E Ch. 3.2 - Prob. 96E Ch. 3.2 - Prob. 97E Ch. 3.2 - Prob. 98E Ch. 3.2 - Prob. 99E Ch. 3.2 - Prob. 100E Ch. 3.2 - Prob. 101E Ch. 3.2 - Prob. 102E Ch. 3.2 - Prob. 103E Ch. 3.2 - Prob. 104E Ch. 3.2 - Prob. 105E Ch. 3.2 - Prob. 106E Ch. 3.2 - Prob. 107E Ch. 3.2 - Prob. 108E Ch. 3.2 - Prob. 109E Ch. 3.2 - Prob. 110E Ch. 3.2 - Prob. 111E Ch. 3.2 - Prob. 112E Ch. 3.2 - Prob. 113E Ch. 3.2 - Prob. 114E Ch. 3.2 - Prob. 115E Ch. 3.2 - Prob. 116E Ch. 3.2 - Prob. 117E Ch. 3.2 - Prob. 118E Ch. 3.2 - Prob. 119E Ch. 3.2 - Prob. 120E Ch. 3.2 - Prob. 121E Ch. 3.2 - Prob. 122E Ch. 3.2 - Prob. 123E Ch. 3.2 - Prob. 124E Ch. 3.2 - Prob. 125E Ch. 3.2 - Prob. 126E Ch. 3.2 - Prob. 127E Ch. 3.2 - Prob. 128E Ch. 3.2 - Prob. 129E Ch. 3.2 - Prob. 130E Ch. 3.2 - Prob. 131E Ch. 3.2 - Prob. 132E Ch. 3.2 - Prob. 133E Ch. 3.2 - Prob. 134E Ch. 3.3 - Prob. 1E Ch. 3.3 - Prob. 2E Ch. 3.3 - Prob. 3E Ch. 3.3 - Prob. 4E Ch. 3.3 - Prob. 5E Ch. 3.3 - Prob. 6E Ch. 3.3 - Prob. 7E Ch. 3.3 - Prob. 8E Ch. 3.3 - Prob. 9E Ch. 3.3 - Prob. 10E Ch. 3.3 - Prob. 11E Ch. 3.3 - Prob. 12E Ch. 3.3 - Prob. 13E Ch. 3.3 - Prob. 14E Ch. 3.3 - Prob. 15E Ch. 3.3 - Prob. 16E Ch. 3.3 - Prob. 17E Ch. 3.3 - Prob. 18E Ch. 3.3 - Prob. 19E Ch. 3.3 - Prob. 20E Ch. 3.3 - Prob. 21E Ch. 3.3 - Prob. 22E Ch. 3.3 - Prob. 23E Ch. 3.3 - Prob. 24E Ch. 3.3 - Prob. 25E Ch. 3.3 - Prob. 26E Ch. 3.3 - Prob. 27E Ch. 3.3 - Prob. 28E Ch. 3.3 - Prob. 29E Ch. 3.3 - Prob. 30E Ch. 3.3 - Prob. 31E Ch. 3.3 - Prob. 32E Ch. 3.3 - Prob. 33E Ch. 3.3 - Prob. 34E Ch. 3.3 - Prob. 35E Ch. 3.3 - Prob. 36E Ch. 3.3 - Prob. 37E Ch. 3.3 - Prob. 38E Ch. 3.3 - Prob. 39E Ch. 3.3 - Prob. 40E Ch. 3.3 - Prob. 41E Ch. 3.3 - Prob. 42E Ch. 3.3 - Prob. 43E Ch. 3.3 - Prob. 44E Ch. 3.3 - Prob. 45E Ch. 3.3 - Prob. 46E Ch. 3.3 - Prob. 47E Ch. 3.3 - Prob. 48E Ch. 3.3 - Prob. 49E Ch. 3.3 - Prob. 50E Ch. 3.3 - Prob. 51E Ch. 3.3 - Prob. 52E Ch. 3.3 - Prob. 53E Ch. 3.3 - Prob. 54E Ch. 3.3 - Prob. 55E Ch. 3.3 - Prob. 56E Ch. 3.3 - Prob. 57E Ch. 3.3 - Prob. 58E Ch. 3.3 - Prob. 59E Ch. 3.3 - Prob. 60E Ch. 3.3 - Prob. 61E Ch. 3.3 - Prob. 62E Ch. 3.3 - Prob. 63E Ch. 3.3 - Prob. 64E Ch. 3.3 - Prob. 65E Ch. 3.3 - Prob. 66E Ch. 3.3 - Prob. 67E Ch. 3.3 - Prob. 68E Ch. 3.3 - Prob. 69E Ch. 3.3 - Prob. 70E Ch. 3.3 - Prob. 71E Ch. 3.3 - Prob. 72E Ch. 3.3 - Prob. 73E Ch. 3.3 - Prob. 74E Ch. 3.3 - Prob. 75E Ch. 3.3 - Prob. 76E Ch. 3.3 - Prob. 77E Ch. 3.3 - Prob. 78E Ch. 3.3 - Prob. 79E Ch. 3.3 - Prob. 80E Ch. 3.3 - Prob. 81E Ch. 3.3 - Prob. 82E Ch. 3.3 - Prob. 83E Ch. 3.3 - Prob. 84E Ch. 3.3 - Prob. 85E Ch. 3.3 - Prob. 86E Ch. 3.3 - Prob. 87E Ch. 3.3 - Prob. 88E Ch. 3.3 - Prob. 89E Ch. 3.3 - Prob. 90E Ch. 3.3 - Prob. 91E Ch. 3.3 - Prob. 92E Ch. 3.3 - Prob. 93E Ch. 3.3 - Prob. 94E Ch. 3.3 - Prob. 97E Ch. 3.3 - Prob. 98E Ch. 3.3 - Prob. 99E Ch. 3.3 - Prob. 100E Ch. 3.3 - Prob. 101E Ch. 3.3 - Prob. 102E Ch. 3.3 - Prob. 103E Ch. 3.3 - Prob. 104E Ch. 3.3 - Prob. 105E Ch. 3.3 - Prob. 106E Ch. 3.3 - Prob. 107E Ch. 3.3 - Prob. 108E Ch. 3.3 - Prob. 109E Ch. 3.3 - Prob. 110E Ch. 3.3 - Prob. 111E Ch. 3.3 - Prob. 112E Ch. 3.4 - Prob. 1E Ch. 3.4 - Prob. 2E Ch. 3.4 - Prob. 3E Ch. 3.4 - Prob. 4E Ch. 3.4 - Prob. 5E Ch. 3.4 - Prob. 6E Ch. 3.4 - Prob. 7E Ch. 3.4 - Prob. 8E Ch. 3.4 - Prob. 9E Ch. 3.4 - Prob. 10E Ch. 3.4 - Prob. 11E Ch. 3.4 - Prob. 12E Ch. 3.4 - Prob. 13E Ch. 3.4 - Prob. 14E Ch. 3.4 - Prob. 15E Ch. 3.4 - Prob. 16E Ch. 3.4 - Prob. 17E Ch. 3.4 - Prob. 18E Ch. 3.4 - Prob. 19E Ch. 3.4 - Prob. 20E Ch. 3.4 - Prob. 21E Ch. 3.4 - Prob. 22E Ch. 3.4 - Prob. 23E Ch. 3.4 - Prob. 24E Ch. 3.4 - Prob. 25E Ch. 3.4 - Prob. 26E Ch. 3.4 - Prob. 27E Ch. 3.4 - Prob. 28E Ch. 3.4 - Prob. 29E Ch. 3.4 - Prob. 30E Ch. 3.4 - Prob. 31E Ch. 3.4 - Prob. 32E Ch. 3.4 - Prob. 33E Ch. 3.4 - Prob. 34E Ch. 3.4 - Prob. 35E Ch. 3.4 - Prob. 36E Ch. 3.4 - Prob. 37E Ch. 3.4 - Prob. 38E Ch. 3.4 - Prob. 39E Ch. 3.4 - Prob. 40E Ch. 3.4 - Prob. 41E Ch. 3.4 - Prob. 42E Ch. 3.4 - Prob. 43E Ch. 3.4 - Prob. 44E Ch. 3.4 - Prob. 45E Ch. 3.4 - Prob. 46E Ch. 3.4 - Prob. 47E Ch. 3.4 - Prob. 48E Ch. 3.4 - Prob. 49E Ch. 3.4 - Prob. 50E Ch. 3.4 - Prob. 51E Ch. 3.4 - Prob. 52E Ch. 3.4 - Prob. 53E Ch. 3.4 - Prob. 54E Ch. 3.4 - Prob. 55E Ch. 3.4 - Prob. 56E Ch. 3.4 - Prob. 57E Ch. 3.4 - Prob. 58E Ch. 3.4 - Prob. 59E Ch. 3.4 - Prob. 60E Ch. 3.4 - Prob. 61E Ch. 3.4 - Prob. 62E Ch. 3.4 - Prob. 63E Ch. 3.4 - Prob. 64E Ch. 3.4 - Prob. 65E Ch. 3.4 - Prob. 66E Ch. 3.4 - Prob. 67E Ch. 3.4 - Prob. 68E Ch. 3.4 - Prob. 69E Ch. 3.4 - Prob. 70E Ch. 3.4 - Prob. 71E Ch. 3.4 - Prob. 72E Ch. 3.4 - Prob. 73E Ch. 3.4 - Prob. 74E Ch. 3.4 - Prob. 75E Ch. 3.4 - Prob. 76E Ch. 3.4 - Prob. 77E Ch. 3.4 - Prob. 78E Ch. 3.4 - Prob. 79E Ch. 3.4 - Prob. 80E Ch. 3.4 - Prob. 81E Ch. 3.4 - Prob. 82E Ch. 3.4 - Prob. 83E Ch. 3.4 - Prob. 84E Ch. 3.4 - Prob. 85E Ch. 3.4 - Prob. 86E Ch. 3.4 - Prob. 87E Ch. 3.4 - Prob. 88E Ch. 3.4 - Prob. 89E Ch. 3.4 - Prob. 90E Ch. 3.4 - Prob. 91E Ch. 3.4 - Prob. 92E Ch. 3.4 - Prob. 93E Ch. 3.4 - Prob. 94E Ch. 3.4 - Prob. 95E Ch. 3.4 - Prob. 96E Ch. 3.4 - Prob. 97E Ch. 3.4 - Prob. 98E Ch. 3.4 - Prob. 99E Ch. 3.4 - Prob. 100E Ch. 3.4 - Prob. 101E Ch. 3.4 - Prob. 102E Ch. 3.4 - Prob. 103E Ch. 3.4 - Prob. 104E Ch. 3.4 - Prob. 105E Ch. 3.4 - Prob. 106E Ch. 3.4 - Prob. 107E Ch. 3.4 - Prob. 108E Ch. 3.4 - Prob. 109E Ch. 3.4 - Prob. 110E Ch. 3.4 - Prob. 111E Ch. 3.4 - Prob. 112E Ch. 3.4 - Prob. 113E Ch. 3.4 - Prob. 114E Ch. 3.4 - Prob. 115E Ch. 3.4 - Prob. 116E Ch. 3.4 - Prob. 117E Ch. 3.4 - Prob. 118E Ch. 3.4 - Prob. 119E Ch. 3.4 - Prob. 120E Ch. 3.4 - Prob. 121E Ch. 3.4 - Prob. 122E Ch. 3.4 - Prob. 123E Ch. 3.4 - Prob. 124E Ch. 3.4 - Prob. 125E Ch. 3.4 - Prob. 126E Ch. 3.4 - Prob. 127E Ch. 3.4 - Prob. 128E Ch. 3.4 - Prob. 129E Ch. 3.4 - Prob. 130E Ch. 3.4 - Prob. 131E Ch. 3.4 - Prob. 132E Ch. 3.4 - Prob. 133E Ch. 3.4 - Prob. 134E Ch. 3.4 - Prob. 135E Ch. 3.4 - Prob. 136E Ch. 3.4 - Prob. 137E Ch. 3.4 - Prob. 138E Ch. 3.4 - Prob. 139E Ch. 3.4 - Prob. 140E Ch. 3.4 - Prob. 141E Ch. 3.4 - Prob. 142E Ch. 3.4 - Prob. 143E Ch. 3.4 - Prob. 144E Ch. 3.4 - Prob. 145E Ch. 3.4 - Prob. 146E Ch. 3.5 - Prob. 1E Ch. 3.5 - Prob. 2E Ch. 3.5 - Prob. 3E Ch. 3.5 - Prob. 4E Ch. 3.5 - Prob. 5E Ch. 3.5 - Prob. 6E Ch. 3.5 - Prob. 7E Ch. 3.5 - Prob. 8E Ch. 3.5 - Prob. 9E Ch. 3.5 - Prob. 10E Ch. 3.5 - Prob. 11E Ch. 3.5 - Prob. 12E Ch. 3.5 - Prob. 13E Ch. 3.5 - Prob. 14E Ch. 3.5 - Prob. 15E Ch. 3.5 - Prob. 16E Ch. 3.5 - Prob. 17E Ch. 3.5 - Prob. 18E Ch. 3.5 - Prob. 19E Ch. 3.5 - Prob. 20E Ch. 3.5 - Prob. 21E Ch. 3.5 - Prob. 22E Ch. 3.5 - Prob. 23E Ch. 3.5 - Prob. 24E Ch. 3.5 - Prob. 25E Ch. 3.5 - Prob. 26E Ch. 3.5 - Prob. 27E Ch. 3.5 - Prob. 28E Ch. 3.5 - Prob. 29E Ch. 3.5 - Prob. 30E Ch. 3.5 - Prob. 31E Ch. 3.5 - Prob. 32E Ch. 3.5 - Prob. 33E Ch. 3.5 - Prob. 34E Ch. 3.5 - Prob. 35E Ch. 3.5 - Prob. 36E Ch. 3.5 - Prob. 37E Ch. 3.5 - Prob. 38E Ch. 3.5 - Prob. 39E Ch. 3.5 - Prob. 40E Ch. 3.5 - Prob. 41E Ch. 3.5 - Prob. 42E Ch. 3.5 - Prob. 43E Ch. 3.5 - Prob. 44E Ch. 3.5 - Prob. 45E Ch. 3.5 - Prob. 46E Ch. 3.5 - Prob. 47E Ch. 3.5 - Prob. 48E Ch. 3.5 - Prob. 49E Ch. 3.5 - Prob. 50E Ch. 3.5 - Prob. 51E Ch. 3.5 - Prob. 52E Ch. 3.5 - Prob. 53E Ch. 3.5 - Prob. 54E Ch. 3.5 - Prob. 55E Ch. 3.5 - Prob. 56E Ch. 3.5 - Prob. 57E Ch. 3.5 - Prob. 58E Ch. 3.5 - Prob. 59E Ch. 3.5 - Prob. 60E Ch. 3.5 - Prob. 61E Ch. 3.5 - Prob. 62E Ch. 3.5 - Prob. 63E Ch. 3.5 - Prob. 64E Ch. 3.5 - Prob. 65E Ch. 3.5 - Prob. 66E Ch. 3.5 - Prob. 67E Ch. 3.5 - Prob. 68E Ch. 3.5 - Prob. 69E Ch. 3.5 - Prob. 70E Ch. 3.5 - Prob. 71E Ch. 3.5 - Prob. 72E Ch. 3.5 - Prob. 73E Ch. 3.5 - Prob. 74E Ch. 3.5 - Prob. 75E Ch. 3.5 - Prob. 76E Ch. 3.5 - Prob. 77E Ch. 3.5 - Prob. 78E Ch. 3.6 - Prob. 1E Ch. 3.6 - Prob. 2E Ch. 3.6 - Prob. 3E Ch. 3.6 - Prob. 4E Ch. 3.6 - Prob. 5E Ch. 3.6 - Prob. 6E Ch. 3.6 - Prob. 7E Ch. 3.6 - Prob. 8E Ch. 3.6 - Prob. 9E Ch. 3.6 - Prob. 10E Ch. 3.6 - Prob. 11E Ch. 3.6 - Prob. 12E Ch. 3.6 - Prob. 13E Ch. 3.6 - Prob. 14E Ch. 3.6 - Prob. 15E Ch. 3.6 - Prob. 16E Ch. 3.6 - Prob. 17E Ch. 3.6 - Prob. 18E Ch. 3.6 - Prob. 19E Ch. 3.6 - Prob. 20E Ch. 3.6 - Prob. 21E Ch. 3.6 - Prob. 22E Ch. 3.6 - Prob. 23E Ch. 3.6 - Prob. 24E Ch. 3.6 - Prob. 25E Ch. 3.6 - Prob. 26E Ch. 3.6 - Prob. 27E Ch. 3.6 - Prob. 28E Ch. 3.6 - Prob. 29E Ch. 3.6 - Prob. 30E Ch. 3.6 - Prob. 31E Ch. 3.6 - Prob. 32E Ch. 3.6 - Prob. 33E Ch. 3.6 - Prob. 34E Ch. 3.6 - Prob. 35E Ch. 3.6 - Prob. 36E Ch. 3.6 - Prob. 37E Ch. 3.6 - Prob. 38E Ch. 3.6 - Prob. 39E Ch. 3.6 - Prob. 40E Ch. 3.6 - Prob. 41E Ch. 3.6 - Prob. 42E Ch. 3.6 - Prob. 43E Ch. 3.6 - Prob. 44E Ch. 3.6 - Prob. 45E Ch. 3.6 - Prob. 46E Ch. 3 - Prob. 1CR Ch. 3 - Prob. 2CR Ch. 3 - Prob. 3CR Ch. 3 - Prob. 4CR Ch. 3 - Prob. 5CR Ch. 3 - Prob. 6CR Ch. 3 - Prob. 7CR Ch. 3 - Prob. 8CR Ch. 3 - Prob. 9CR Ch. 3 - Prob. 10CR Ch. 3 - Prob. 11CR Ch. 3 - Prob. 12CR Ch. 3 - Prob. 13CR Ch. 3 - Prob. 14CR Ch. 3 - Prob. 15CR Ch. 3 - Prob. 16CR Ch. 3 - Prob. 17CR Ch. 3 - Prob. 18CR Ch. 3 - Prob. 19CR Ch. 3 - Prob. 20CR Ch. 3 - Prob. 21CR Ch. 3 - Prob. 22CR Ch. 3 - Prob. 23CR Ch. 3 - Prob. 24CR Ch. 3 - Prob. 25CR Ch. 3 - Prob. 26CR Ch. 3 - Prob. 27CR Ch. 3 - Prob. 28CR Ch. 3 - Prob. 29CR Ch. 3 - Prob. 30CR Ch. 3 - Prob. 31CR Ch. 3 - Prob. 32CR Ch. 3 - Prob. 33CR Ch. 3 - Prob. 34CR Ch. 3 - Prob. 35CR Ch. 3 - Prob. 36CR Ch. 3 - Prob. 37CR Ch. 3 - Prob. 38CR Ch. 3 - Prob. 39CR Ch. 3 - Prob. 40CR Ch. 3 - Prob. 41CR Ch. 3 - Prob. 42CR Ch. 3 - Prob. 43CR Ch. 3 - Prob. 44CR Ch. 3 - Prob. 45CR Ch. 3 - Prob. 46CR Ch. 3 - Prob. 47CR Ch. 3 - Prob. 48CR Ch. 3 - Prob. 49CR Ch. 3 - Prob. 50CR Ch. 3 - Prob. 51CR Ch. 3 - Prob. 52CR Ch. 3 - Prob. 53CR Ch. 3 - Prob. 54CR Ch. 3 - Prob. 55CR Ch. 3 - Prob. 56CR Ch. 3 - Prob. 57CR Ch. 3 - Prob. 58CR Ch. 3 - Prob. 59CR Ch. 3 - Prob. 60CR Ch. 3 - Prob. 61CR Ch. 3 - Prob. 62CR Ch. 3 - Prob. 63CR Ch. 3 - Prob. 64CR Ch. 3 - Prob. 65CR Ch. 3 - Prob. 66CR Ch. 3 - Prob. 67CR Ch. 3 - Prob. 68CR Ch. 3 - Prob. 69CR Ch. 3 - Prob. 70CR Ch. 3 - Prob. 71CR Ch. 3 - Prob. 72CR Ch. 3 - Prob. 73CR Ch. 3 - Prob. 74CR Ch. 3 - Prob. 75CR Ch. 3 - Prob. 76CR Ch. 3 - Prob. 77CR Ch. 3 - Prob. 78CR Ch. 3 - Prob. 79CR Ch. 3 - Prob. 80CR Ch. 3 - Prob. 81CR Ch. 3 - Prob. 82CR Ch. 3 - Prob. 83CR Ch. 3 - Prob. 84CR Ch. 3 - Prob. 85CR Ch. 3 - Prob. 86CR Ch. 3 - Prob. 87CR Ch. 3 - Prob. 88CR Ch. 3 - Prob. 89CR Ch. 3 - Prob. 90CR Ch. 3 - Prob. 91CR Ch. 3 - Prob. 92CR Ch. 3 - Prob. 93CR Ch. 3 - Prob. 94CR Ch. 3 - Prob. 95CR Ch. 3 - Prob. 96CR Ch. 3 - Prob. 97CR Ch. 3 - Prob. 98CR Ch. 3 - Prob. 99CR Ch. 3 - Prob. 100CR Ch. 3 - Prob. 101CR Ch. 3 - Prob. 102CR Ch. 3 - Prob. 103CR Ch. 3 - Prob. 104CR Ch. 3 - Prob. 105CR Ch. 3 - Prob. 106CR Ch. 3 - Prob. 107CR Ch. 3 - Prob. 108CR Ch. 3 - Prob. 109CR Ch. 3 - Prob. 110CR Ch. 3 - Prob. 111CR Ch. 3 - Prob. 112CR Ch. 3 - Prob. 113CR Ch. 3 - Prob. 114CR Ch. 3 - Prob. 115CR Ch. 3 - Prob. 116CR Ch. 3 - Prob. 117CR Ch. 3 - Prob. 118CR Ch. 3 - Prob. 119CR Ch. 3 - Prob. 120CR Ch. 3 - Prob. 121CR Ch. 3 - Prob. 122CR Ch. 3 - Prob. 123CR Ch. 3 - Prob. 124CR Ch. 3 - Prob. 125CR Ch. 3 - Prob. 126CR Ch. 3 - Prob. 1CT Ch. 3 - Prob. 2CT Ch. 3 - Prob. 3CT Ch. 3 - Prob. 4CT Ch. 3 - Prob. 5CT Ch. 3 - Prob. 6CT Ch. 3 - Prob. 7CT Ch. 3 - Prob. 8CT Ch. 3 - Prob. 9CT Ch. 3 - Prob. 10CT Ch. 3 - Prob. 11CT Ch. 3 - Prob. 12CT Ch. 3 - Prob. 13CT Ch. 3 - Prob. 14CT Ch. 3 - Prob. 15CT Ch. 3 - Prob. 16CT Ch. 3 - Prob. 17CT Ch. 3 - Prob. 18CT Ch. 3 - Prob. 19CT Ch. 3 - Prob. 20CT Ch. 3 - Prob. 21CT Ch. 3 - Prob. 22CT Ch. 3 - Prob. 23CT Ch. 3 - Prob. 24CT Ch. 3 - Prob. 25CT Ch. 3 - Prob. 26CT Ch. 3 - Prob. 27CT Ch. 3 - Prob. 28CT Ch. 3 - Prob. 29CT Ch. 3 - Prob. 30CT Ch. 3 - Prob. 1STP Ch. 3 - Prob. 2STP Ch. 3 - Prob. 3STP Ch. 3 - Prob. 4STP Ch. 3 - Prob. 5STP Ch. 3 - Prob. 6STP Ch. 3 - Prob. 7STP Ch. 3 - Prob. 8STP Ch. 3 - Prob. 9STP Ch. 3 - Prob. 10STP Ch. 3 - Prob. 11STP Ch. 3 - Prob. 12STP Ch. 3 - Prob. 13STP Ch. 3 - Prob. 14STP Ch. 3 - Prob. 15STP Ch. 3 - Prob. 16STP Ch. 3 - Prob. 17STP Ch. 3 - Prob. 18STP Ch. 3 - Prob. 19STP Ch. 3 - Prob. 20STP Ch. 3 - Prob. 21STP Ch. 3 - Prob. 22STP Ch. 3 - Prob. 23STP Ch. 3 - Prob. 24STP Ch. 3 - Prob. 25STP Ch. 3 - Prob. 26STP

Knowledge Booster

$Calculus$

Learn more about

Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.