EP PRECALC.GRAPHING APPR.-WEBASSIGN-1YR
EP PRECALC.GRAPHING APPR.-WEBASSIGN-1YR
8th Edition
ISBN: 9780357022078
Author: Larson
Publisher: CENGAGE L
bartleby

Concept explainers

Minimization
In mathematics, traditional optimization problems are typically expressed in terms of minimization. When we talk about minimizing or maximizing a function, we refer to the maximum and minimum possible values of that function. This can be expressed in ter…
Maxima and Minima
The extreme points of a function are the maximum and the minimum points of the function. A maximum is attained when the function takes the maximum value and a minimum is attained when the function takes the minimum value.
Derivatives
A derivative means a change. Geometrically it can be represented as a line with some steepness. Imagine climbing a mountain which is very steep and 500 meters high. Is it easier to climb? Definitely not! Suppose walking on the road for 500 meters. Which …
Concavity
In calculus, concavity is a descriptor of mathematics that tells about the shape of the graph. It is the parameter that helps to estimate the maximum and minimum value of any of the functions and the concave nature using the graphical method. We use the …
bartleby

Videos

Question
Book Icon
Chapter 3.2, Problem 91E
To determine

To find:

The domain, vertical asymptote, and x -intercept of the given logarithmic function. Sketch the graph of function.

Expert Solution & Answer
Check Mark

Answer to Problem 91E

Domain: (−∞,0) ,

Vertical asymptote: x=0 ,

The x -intercept: (−1,0) .

Explanation of Solution

Given:

A logarithm function: g(x)=ln(−x).

Calculation:

We know that logarithmic functions are not defined for negative values. To find domain of our given function, we will set argument of log function greater than 0 as:

  −x>0x<0

Therefore, the domain of our given logarithmic function would be x<0 or (−∞,0).

We know that logarithmic functions are not defined at 0. To find vertical asymptote, we will set argument of logarithmic function equal to 0 as:

  −x=0x=0

Therefore, the given logarithmic function has a vertical asymptote at x=0.

To find the x -intercept of our given function, we will set y=0 and solve for x as:

  ln(−x)=0e0=−x (Converting log to exponetial form)1=−xx=−1

Therefore, the x- intercept of our given logarithmic function is (−1,0).

Upon graphing our given logarithmic function, we will get our required graph as shown below:

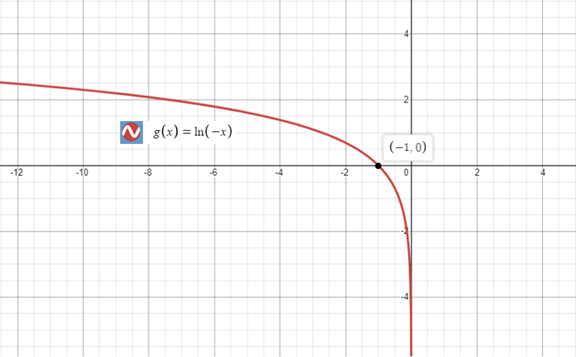
  EP PRECALC.GRAPHING APPR.-WEBASSIGN-1YR, Chapter 3.2, Problem 91E

Previous
Chapter 3.2, Problem 90E
Next
Chapter 3.2, Problem 92E

Chapter 3 Solutions

EP PRECALC.GRAPHING APPR.-WEBASSIGN-1YR

Ch. 3.1 - Prob. 1ECh. 3.1 - Prob. 2ECh. 3.1 - Prob. 3ECh. 3.1 - Prob. 4ECh. 3.1 - Prob. 5ECh. 3.1 - Prob. 6ECh. 3.1 - Prob. 7ECh. 3.1 - Prob. 8ECh. 3.1 - Prob. 9ECh. 3.1 - Prob. 10E
Ch. 3.1 - Prob. 11ECh. 3.1 - Prob. 12ECh. 3.1 - Prob. 13ECh. 3.1 - Prob. 14ECh. 3.1 - Prob. 15ECh. 3.1 - Prob. 16ECh. 3.1 - Prob. 17ECh. 3.1 - Prob. 18ECh. 3.1 - Prob. 19ECh. 3.1 - Prob. 20ECh. 3.1 - Prob. 21ECh. 3.1 - Prob. 22ECh. 3.1 - Prob. 23ECh. 3.1 - Prob. 24ECh. 3.1 - Prob. 25ECh. 3.1 - Prob. 26ECh. 3.1 - Prob. 27ECh. 3.1 - Prob. 28ECh. 3.1 - Prob. 29ECh. 3.1 - Prob. 30ECh. 3.1 - Prob. 31ECh. 3.1 - Prob. 32ECh. 3.1 - Prob. 33ECh. 3.1 - Prob. 34ECh. 3.1 - Prob. 35ECh. 3.1 - Prob. 36ECh. 3.1 - Prob. 37ECh. 3.1 - Prob. 38ECh. 3.1 - Prob. 39ECh. 3.1 - Prob. 40ECh. 3.1 - Prob. 41ECh. 3.1 - Prob. 42ECh. 3.1 - Prob. 43ECh. 3.1 - Prob. 44ECh. 3.1 - Prob. 45ECh. 3.1 - Prob. 46ECh. 3.1 - Prob. 47ECh. 3.1 - Prob. 48ECh. 3.1 - Prob. 49ECh. 3.1 - Prob. 50ECh. 3.1 - Prob. 51ECh. 3.1 - Prob. 52ECh. 3.1 - Prob. 53ECh. 3.1 - Prob. 54ECh. 3.1 - Prob. 55ECh. 3.1 - Prob. 56ECh. 3.1 - Prob. 57ECh. 3.1 - Prob. 58ECh. 3.1 - Prob. 59ECh. 3.1 - Prob. 60ECh. 3.1 - Prob. 61ECh. 3.1 - Prob. 62ECh. 3.1 - Prob. 63ECh. 3.1 - Prob. 64ECh. 3.1 - Prob. 65ECh. 3.1 - Prob. 66ECh. 3.1 - Prob. 67ECh. 3.1 - Prob. 68ECh. 3.1 - Prob. 69ECh. 3.1 - Prob. 70ECh. 3.1 - Prob. 71ECh. 3.1 - Prob. 72ECh. 3.1 - Prob. 73ECh. 3.1 - Prob. 74ECh. 3.1 - Prob. 75ECh. 3.1 - Prob. 76ECh. 3.1 - Prob. 77ECh. 3.1 - Prob. 78ECh. 3.1 - Prob. 79ECh. 3.1 - Prob. 80ECh. 3.1 - Prob. 81ECh. 3.1 - Prob. 82ECh. 3.1 - Prob. 83ECh. 3.1 - Prob. 84ECh. 3.1 - Prob. 85ECh. 3.1 - Prob. 86ECh. 3.1 - Prob. 87ECh. 3.1 - Prob. 88ECh. 3.1 - Prob. 89ECh. 3.1 - Prob. 90ECh. 3.1 - Prob. 91ECh. 3.1 - Prob. 92ECh. 3.1 - Prob. 93ECh. 3.2 - Prob. 1ECh. 3.2 - Prob. 2ECh. 3.2 - Prob. 3ECh. 3.2 - Prob. 4ECh. 3.2 - Prob. 5ECh. 3.2 - Prob. 6ECh. 3.2 - Prob. 7ECh. 3.2 - Prob. 8ECh. 3.2 - Prob. 9ECh. 3.2 - Prob. 10ECh. 3.2 - Prob. 11ECh. 3.2 - Prob. 12ECh. 3.2 - Prob. 13ECh. 3.2 - Prob. 14ECh. 3.2 - Prob. 15ECh. 3.2 - Prob. 16ECh. 3.2 - Prob. 17ECh. 3.2 - Prob. 18ECh. 3.2 - Prob. 19ECh. 3.2 - Prob. 20ECh. 3.2 - Prob. 21ECh. 3.2 - Prob. 22ECh. 3.2 - Prob. 23ECh. 3.2 - Prob. 24ECh. 3.2 - Prob. 25ECh. 3.2 - Prob. 26ECh. 3.2 - Prob. 27ECh. 3.2 - Prob. 28ECh. 3.2 - Prob. 29ECh. 3.2 - Prob. 30ECh. 3.2 - Prob. 31ECh. 3.2 - Prob. 32ECh. 3.2 - Prob. 33ECh. 3.2 - Prob. 34ECh. 3.2 - Prob. 35ECh. 3.2 - Prob. 36ECh. 3.2 - Prob. 37ECh. 3.2 - Prob. 38ECh. 3.2 - Prob. 39ECh. 3.2 - Prob. 40ECh. 3.2 - Prob. 41ECh. 3.2 - Prob. 42ECh. 3.2 - Prob. 43ECh. 3.2 - Prob. 44ECh. 3.2 - Prob. 45ECh. 3.2 - Prob. 46ECh. 3.2 - Prob. 47ECh. 3.2 - Prob. 48ECh. 3.2 - Prob. 49ECh. 3.2 - Prob. 50ECh. 3.2 - Prob. 51ECh. 3.2 - Prob. 52ECh. 3.2 - Prob. 53ECh. 3.2 - Prob. 54ECh. 3.2 - Prob. 55ECh. 3.2 - Prob. 56ECh. 3.2 - Prob. 57ECh. 3.2 - Prob. 58ECh. 3.2 - Prob. 59ECh. 3.2 - Prob. 60ECh. 3.2 - Prob. 61ECh. 3.2 - Prob. 62ECh. 3.2 - Prob. 63ECh. 3.2 - Prob. 64ECh. 3.2 - Prob. 65ECh. 3.2 - Prob. 66ECh. 3.2 - Prob. 67ECh. 3.2 - Prob. 68ECh. 3.2 - Prob. 69ECh. 3.2 - Prob. 70ECh. 3.2 - Prob. 71ECh. 3.2 - Prob. 72ECh. 3.2 - Prob. 73ECh. 3.2 - Prob. 74ECh. 3.2 - Prob. 75ECh. 3.2 - Prob. 76ECh. 3.2 - Prob. 77ECh. 3.2 - Prob. 78ECh. 3.2 - Prob. 79ECh. 3.2 - Prob. 80ECh. 3.2 - Prob. 81ECh. 3.2 - Prob. 82ECh. 3.2 - Prob. 83ECh. 3.2 - Prob. 84ECh. 3.2 - Prob. 85ECh. 3.2 - Prob. 86ECh. 3.2 - Prob. 87ECh. 3.2 - Prob. 88ECh. 3.2 - Prob. 89ECh. 3.2 - Prob. 90ECh. 3.2 - Prob. 91ECh. 3.2 - Prob. 92ECh. 3.2 - Prob. 93ECh. 3.2 - Prob. 94ECh. 3.2 - Prob. 95ECh. 3.2 - Prob. 96ECh. 3.2 - Prob. 97ECh. 3.2 - Prob. 98ECh. 3.2 - Prob. 99ECh. 3.2 - Prob. 100ECh. 3.2 - Prob. 101ECh. 3.2 - Prob. 102ECh. 3.2 - Prob. 103ECh. 3.2 - Prob. 104ECh. 3.2 - Prob. 105ECh. 3.2 - Prob. 106ECh. 3.2 - Prob. 107ECh. 3.2 - Prob. 108ECh. 3.2 - Prob. 109ECh. 3.2 - Prob. 110ECh. 3.2 - Prob. 111ECh. 3.2 - Prob. 112ECh. 3.2 - Prob. 113ECh. 3.2 - Prob. 114ECh. 3.2 - Prob. 115ECh. 3.2 - Prob. 116ECh. 3.2 - Prob. 117ECh. 3.2 - Prob. 118ECh. 3.2 - Prob. 119ECh. 3.2 - Prob. 120ECh. 3.2 - Prob. 121ECh. 3.2 - Prob. 122ECh. 3.2 - Prob. 123ECh. 3.2 - Prob. 124ECh. 3.2 - Prob. 125ECh. 3.2 - Prob. 126ECh. 3.2 - Prob. 127ECh. 3.2 - Prob. 128ECh. 3.2 - Prob. 129ECh. 3.2 - Prob. 130ECh. 3.2 - Prob. 131ECh. 3.2 - Prob. 132ECh. 3.2 - Prob. 133ECh. 3.2 - Prob. 134ECh. 3.3 - Prob. 1ECh. 3.3 - Prob. 2ECh. 3.3 - Prob. 3ECh. 3.3 - Prob. 4ECh. 3.3 - Prob. 5ECh. 3.3 - Prob. 6ECh. 3.3 - Prob. 7ECh. 3.3 - Prob. 8ECh. 3.3 - Prob. 9ECh. 3.3 - Prob. 10ECh. 3.3 - Prob. 11ECh. 3.3 - Prob. 12ECh. 3.3 - Prob. 13ECh. 3.3 - Prob. 14ECh. 3.3 - Prob. 15ECh. 3.3 - Prob. 16ECh. 3.3 - Prob. 17ECh. 3.3 - Prob. 18ECh. 3.3 - Prob. 19ECh. 3.3 - Prob. 20ECh. 3.3 - Prob. 21ECh. 3.3 - Prob. 22ECh. 3.3 - Prob. 23ECh. 3.3 - Prob. 24ECh. 3.3 - Prob. 25ECh. 3.3 - Prob. 26ECh. 3.3 - Prob. 27ECh. 3.3 - Prob. 28ECh. 3.3 - Prob. 29ECh. 3.3 - Prob. 30ECh. 3.3 - Prob. 31ECh. 3.3 - Prob. 32ECh. 3.3 - Prob. 33ECh. 3.3 - Prob. 34ECh. 3.3 - Prob. 35ECh. 3.3 - Prob. 36ECh. 3.3 - Prob. 37ECh. 3.3 - Prob. 38ECh. 3.3 - Prob. 39ECh. 3.3 - Prob. 40ECh. 3.3 - Prob. 41ECh. 3.3 - Prob. 42ECh. 3.3 - Prob. 43ECh. 3.3 - Prob. 44ECh. 3.3 - Prob. 45ECh. 3.3 - Prob. 46ECh. 3.3 - Prob. 47ECh. 3.3 - Prob. 48ECh. 3.3 - Prob. 49ECh. 3.3 - Prob. 50ECh. 3.3 - Prob. 51ECh. 3.3 - Prob. 52ECh. 3.3 - Prob. 53ECh. 3.3 - Prob. 54ECh. 3.3 - Prob. 55ECh. 3.3 - Prob. 56ECh. 3.3 - Prob. 57ECh. 3.3 - Prob. 58ECh. 3.3 - Prob. 59ECh. 3.3 - Prob. 60ECh. 3.3 - Prob. 61ECh. 3.3 - Prob. 62ECh. 3.3 - Prob. 63ECh. 3.3 - Prob. 64ECh. 3.3 - Prob. 65ECh. 3.3 - Prob. 66ECh. 3.3 - Prob. 67ECh. 3.3 - Prob. 68ECh. 3.3 - Prob. 69ECh. 3.3 - Prob. 70ECh. 3.3 - Prob. 71ECh. 3.3 - Prob. 72ECh. 3.3 - Prob. 73ECh. 3.3 - Prob. 74ECh. 3.3 - Prob. 75ECh. 3.3 - Prob. 76ECh. 3.3 - Prob. 77ECh. 3.3 - Prob. 78ECh. 3.3 - Prob. 79ECh. 3.3 - Prob. 80ECh. 3.3 - Prob. 81ECh. 3.3 - Prob. 82ECh. 3.3 - Prob. 83ECh. 3.3 - Prob. 84ECh. 3.3 - Prob. 85ECh. 3.3 - Prob. 86ECh. 3.3 - Prob. 87ECh. 3.3 - Prob. 88ECh. 3.3 - Prob. 89ECh. 3.3 - Prob. 90ECh. 3.3 - Prob. 91ECh. 3.3 - Prob. 92ECh. 3.3 - Prob. 93ECh. 3.3 - Prob. 94ECh. 3.3 - Prob. 97ECh. 3.3 - Prob. 98ECh. 3.3 - Prob. 99ECh. 3.3 - Prob. 100ECh. 3.3 - Prob. 101ECh. 3.3 - Prob. 102ECh. 3.3 - Prob. 103ECh. 3.3 - Prob. 104ECh. 3.3 - Prob. 105ECh. 3.3 - Prob. 106ECh. 3.3 - Prob. 107ECh. 3.3 - Prob. 108ECh. 3.3 - Prob. 109ECh. 3.3 - Prob. 110ECh. 3.3 - Prob. 111ECh. 3.3 - Prob. 112ECh. 3.4 - Prob. 1ECh. 3.4 - Prob. 2ECh. 3.4 - Prob. 3ECh. 3.4 - Prob. 4ECh. 3.4 - Prob. 5ECh. 3.4 - Prob. 6ECh. 3.4 - Prob. 7ECh. 3.4 - Prob. 8ECh. 3.4 - Prob. 9ECh. 3.4 - Prob. 10ECh. 3.4 - Prob. 11ECh. 3.4 - Prob. 12ECh. 3.4 - Prob. 13ECh. 3.4 - Prob. 14ECh. 3.4 - Prob. 15ECh. 3.4 - Prob. 16ECh. 3.4 - Prob. 17ECh. 3.4 - Prob. 18ECh. 3.4 - Prob. 19ECh. 3.4 - Prob. 20ECh. 3.4 - Prob. 21ECh. 3.4 - Prob. 22ECh. 3.4 - Prob. 23ECh. 3.4 - Prob. 24ECh. 3.4 - Prob. 25ECh. 3.4 - Prob. 26ECh. 3.4 - Prob. 27ECh. 3.4 - Prob. 28ECh. 3.4 - Prob. 29ECh. 3.4 - Prob. 30ECh. 3.4 - Prob. 31ECh. 3.4 - Prob. 32ECh. 3.4 - Prob. 33ECh. 3.4 - Prob. 34ECh. 3.4 - Prob. 35ECh. 3.4 - Prob. 36ECh. 3.4 - Prob. 37ECh. 3.4 - Prob. 38ECh. 3.4 - Prob. 39ECh. 3.4 - Prob. 40ECh. 3.4 - Prob. 41ECh. 3.4 - Prob. 42ECh. 3.4 - Prob. 43ECh. 3.4 - Prob. 44ECh. 3.4 - Prob. 45ECh. 3.4 - Prob. 46ECh. 3.4 - Prob. 47ECh. 3.4 - Prob. 48ECh. 3.4 - Prob. 49ECh. 3.4 - Prob. 50ECh. 3.4 - Prob. 51ECh. 3.4 - Prob. 52ECh. 3.4 - Prob. 53ECh. 3.4 - Prob. 54ECh. 3.4 - Prob. 55ECh. 3.4 - Prob. 56ECh. 3.4 - Prob. 57ECh. 3.4 - Prob. 58ECh. 3.4 - Prob. 59ECh. 3.4 - Prob. 60ECh. 3.4 - Prob. 61ECh. 3.4 - Prob. 62ECh. 3.4 - Prob. 63ECh. 3.4 - Prob. 64ECh. 3.4 - Prob. 65ECh. 3.4 - Prob. 66ECh. 3.4 - Prob. 67ECh. 3.4 - Prob. 68ECh. 3.4 - Prob. 69ECh. 3.4 - Prob. 70ECh. 3.4 - Prob. 71ECh. 3.4 - Prob. 72ECh. 3.4 - Prob. 73ECh. 3.4 - Prob. 74ECh. 3.4 - Prob. 75ECh. 3.4 - Prob. 76ECh. 3.4 - Prob. 77ECh. 3.4 - Prob. 78ECh. 3.4 - Prob. 79ECh. 3.4 - Prob. 80ECh. 3.4 - Prob. 81ECh. 3.4 - Prob. 82ECh. 3.4 - Prob. 83ECh. 3.4 - Prob. 84ECh. 3.4 - Prob. 85ECh. 3.4 - Prob. 86ECh. 3.4 - Prob. 87ECh. 3.4 - Prob. 88ECh. 3.4 - Prob. 89ECh. 3.4 - Prob. 90ECh. 3.4 - Prob. 91ECh. 3.4 - Prob. 92ECh. 3.4 - Prob. 93ECh. 3.4 - Prob. 94ECh. 3.4 - Prob. 95ECh. 3.4 - Prob. 96ECh. 3.4 - Prob. 97ECh. 3.4 - Prob. 98ECh. 3.4 - Prob. 99ECh. 3.4 - Prob. 100ECh. 3.4 - Prob. 101ECh. 3.4 - Prob. 102ECh. 3.4 - Prob. 103ECh. 3.4 - Prob. 104ECh. 3.4 - Prob. 105ECh. 3.4 - Prob. 106ECh. 3.4 - Prob. 107ECh. 3.4 - Prob. 108ECh. 3.4 - Prob. 109ECh. 3.4 - Prob. 110ECh. 3.4 - Prob. 111ECh. 3.4 - Prob. 112ECh. 3.4 - Prob. 113ECh. 3.4 - Prob. 114ECh. 3.4 - Prob. 115ECh. 3.4 - Prob. 116ECh. 3.4 - Prob. 117ECh. 3.4 - Prob. 118ECh. 3.4 - Prob. 119ECh. 3.4 - Prob. 120ECh. 3.4 - Prob. 121ECh. 3.4 - Prob. 122ECh. 3.4 - Prob. 123ECh. 3.4 - Prob. 124ECh. 3.4 - Prob. 125ECh. 3.4 - Prob. 126ECh. 3.4 - Prob. 127ECh. 3.4 - Prob. 128ECh. 3.4 - Prob. 129ECh. 3.4 - Prob. 130ECh. 3.4 - Prob. 131ECh. 3.4 - Prob. 132ECh. 3.4 - Prob. 133ECh. 3.4 - Prob. 134ECh. 3.4 - Prob. 135ECh. 3.4 - Prob. 136ECh. 3.4 - Prob. 137ECh. 3.4 - Prob. 138ECh. 3.4 - Prob. 139ECh. 3.4 - Prob. 140ECh. 3.4 - Prob. 141ECh. 3.4 - Prob. 142ECh. 3.4 - Prob. 143ECh. 3.4 - Prob. 144ECh. 3.4 - Prob. 145ECh. 3.4 - Prob. 146ECh. 3.5 - Prob. 1ECh. 3.5 - Prob. 2ECh. 3.5 - Prob. 3ECh. 3.5 - Prob. 4ECh. 3.5 - Prob. 5ECh. 3.5 - Prob. 6ECh. 3.5 - Prob. 7ECh. 3.5 - Prob. 8ECh. 3.5 - Prob. 9ECh. 3.5 - Prob. 10ECh. 3.5 - Prob. 11ECh. 3.5 - Prob. 12ECh. 3.5 - Prob. 13ECh. 3.5 - Prob. 14ECh. 3.5 - Prob. 15ECh. 3.5 - Prob. 16ECh. 3.5 - Prob. 17ECh. 3.5 - Prob. 18ECh. 3.5 - Prob. 19ECh. 3.5 - Prob. 20ECh. 3.5 - Prob. 21ECh. 3.5 - Prob. 22ECh. 3.5 - Prob. 23ECh. 3.5 - Prob. 24ECh. 3.5 - Prob. 25ECh. 3.5 - Prob. 26ECh. 3.5 - Prob. 27ECh. 3.5 - Prob. 28ECh. 3.5 - Prob. 29ECh. 3.5 - Prob. 30ECh. 3.5 - Prob. 31ECh. 3.5 - Prob. 32ECh. 3.5 - Prob. 33ECh. 3.5 - Prob. 34ECh. 3.5 - Prob. 35ECh. 3.5 - Prob. 36ECh. 3.5 - Prob. 37ECh. 3.5 - Prob. 38ECh. 3.5 - Prob. 39ECh. 3.5 - Prob. 40ECh. 3.5 - Prob. 41ECh. 3.5 - Prob. 42ECh. 3.5 - Prob. 43ECh. 3.5 - Prob. 44ECh. 3.5 - Prob. 45ECh. 3.5 - Prob. 46ECh. 3.5 - Prob. 47ECh. 3.5 - Prob. 48ECh. 3.5 - Prob. 49ECh. 3.5 - Prob. 50ECh. 3.5 - Prob. 51ECh. 3.5 - Prob. 52ECh. 3.5 - Prob. 53ECh. 3.5 - Prob. 54ECh. 3.5 - Prob. 55ECh. 3.5 - Prob. 56ECh. 3.5 - Prob. 57ECh. 3.5 - Prob. 58ECh. 3.5 - Prob. 59ECh. 3.5 - Prob. 60ECh. 3.5 - Prob. 61ECh. 3.5 - Prob. 62ECh. 3.5 - Prob. 63ECh. 3.5 - Prob. 64ECh. 3.5 - Prob. 65ECh. 3.5 - Prob. 66ECh. 3.5 - Prob. 67ECh. 3.5 - Prob. 68ECh. 3.5 - Prob. 69ECh. 3.5 - Prob. 70ECh. 3.5 - Prob. 71ECh. 3.5 - Prob. 72ECh. 3.5 - Prob. 73ECh. 3.5 - Prob. 74ECh. 3.5 - Prob. 75ECh. 3.5 - Prob. 76ECh. 3.5 - Prob. 77ECh. 3.5 - Prob. 78ECh. 3.6 - Prob. 1ECh. 3.6 - Prob. 2ECh. 3.6 - Prob. 3ECh. 3.6 - Prob. 4ECh. 3.6 - Prob. 5ECh. 3.6 - Prob. 6ECh. 3.6 - Prob. 7ECh. 3.6 - Prob. 8ECh. 3.6 - Prob. 9ECh. 3.6 - Prob. 10ECh. 3.6 - Prob. 11ECh. 3.6 - Prob. 12ECh. 3.6 - Prob. 13ECh. 3.6 - Prob. 14ECh. 3.6 - Prob. 15ECh. 3.6 - Prob. 16ECh. 3.6 - Prob. 17ECh. 3.6 - Prob. 18ECh. 3.6 - Prob. 19ECh. 3.6 - Prob. 20ECh. 3.6 - Prob. 21ECh. 3.6 - Prob. 22ECh. 3.6 - Prob. 23ECh. 3.6 - Prob. 24ECh. 3.6 - Prob. 25ECh. 3.6 - Prob. 26ECh. 3.6 - Prob. 27ECh. 3.6 - Prob. 28ECh. 3.6 - Prob. 29ECh. 3.6 - Prob. 30ECh. 3.6 - Prob. 31ECh. 3.6 - Prob. 32ECh. 3.6 - Prob. 33ECh. 3.6 - Prob. 34ECh. 3.6 - Prob. 35ECh. 3.6 - Prob. 36ECh. 3.6 - Prob. 37ECh. 3.6 - Prob. 38ECh. 3.6 - Prob. 39ECh. 3.6 - Prob. 40ECh. 3.6 - Prob. 41ECh. 3.6 - Prob. 42ECh. 3.6 - Prob. 43ECh. 3.6 - Prob. 44ECh. 3.6 - Prob. 45ECh. 3.6 - Prob. 46ECh. 3 - Prob. 1CRCh. 3 - Prob. 2CRCh. 3 - Prob. 3CRCh. 3 - Prob. 4CRCh. 3 - Prob. 5CRCh. 3 - Prob. 6CRCh. 3 - Prob. 7CRCh. 3 - Prob. 8CRCh. 3 - Prob. 9CRCh. 3 - Prob. 10CRCh. 3 - Prob. 11CRCh. 3 - Prob. 12CRCh. 3 - Prob. 13CRCh. 3 - Prob. 14CRCh. 3 - Prob. 15CRCh. 3 - Prob. 16CRCh. 3 - Prob. 17CRCh. 3 - Prob. 18CRCh. 3 - Prob. 19CRCh. 3 - Prob. 20CRCh. 3 - Prob. 21CRCh. 3 - Prob. 22CRCh. 3 - Prob. 23CRCh. 3 - Prob. 24CRCh. 3 - Prob. 25CRCh. 3 - Prob. 26CRCh. 3 - Prob. 27CRCh. 3 - Prob. 28CRCh. 3 - Prob. 29CRCh. 3 - Prob. 30CRCh. 3 - Prob. 31CRCh. 3 - Prob. 32CRCh. 3 - Prob. 33CRCh. 3 - Prob. 34CRCh. 3 - Prob. 35CRCh. 3 - Prob. 36CRCh. 3 - Prob. 37CRCh. 3 - Prob. 38CRCh. 3 - Prob. 39CRCh. 3 - Prob. 40CRCh. 3 - Prob. 41CRCh. 3 - Prob. 42CRCh. 3 - Prob. 43CRCh. 3 - Prob. 44CRCh. 3 - Prob. 45CRCh. 3 - Prob. 46CRCh. 3 - Prob. 47CRCh. 3 - Prob. 48CRCh. 3 - Prob. 49CRCh. 3 - Prob. 50CRCh. 3 - Prob. 51CRCh. 3 - Prob. 52CRCh. 3 - Prob. 53CRCh. 3 - Prob. 54CRCh. 3 - Prob. 55CRCh. 3 - Prob. 56CRCh. 3 - Prob. 57CRCh. 3 - Prob. 58CRCh. 3 - Prob. 59CRCh. 3 - Prob. 60CRCh. 3 - Prob. 61CRCh. 3 - Prob. 62CRCh. 3 - Prob. 63CRCh. 3 - Prob. 64CRCh. 3 - Prob. 65CRCh. 3 - Prob. 66CRCh. 3 - Prob. 67CRCh. 3 - Prob. 68CRCh. 3 - Prob. 69CRCh. 3 - Prob. 70CRCh. 3 - Prob. 71CRCh. 3 - Prob. 72CRCh. 3 - Prob. 73CRCh. 3 - Prob. 74CRCh. 3 - Prob. 75CRCh. 3 - Prob. 76CRCh. 3 - Prob. 77CRCh. 3 - Prob. 78CRCh. 3 - Prob. 79CRCh. 3 - Prob. 80CRCh. 3 - Prob. 81CRCh. 3 - Prob. 82CRCh. 3 - Prob. 83CRCh. 3 - Prob. 84CRCh. 3 - Prob. 85CRCh. 3 - Prob. 86CRCh. 3 - Prob. 87CRCh. 3 - Prob. 88CRCh. 3 - Prob. 89CRCh. 3 - Prob. 90CRCh. 3 - Prob. 91CRCh. 3 - Prob. 92CRCh. 3 - Prob. 93CRCh. 3 - Prob. 94CRCh. 3 - Prob. 95CRCh. 3 - Prob. 96CRCh. 3 - Prob. 97CRCh. 3 - Prob. 98CRCh. 3 - Prob. 99CRCh. 3 - Prob. 100CRCh. 3 - Prob. 101CRCh. 3 - Prob. 102CRCh. 3 - Prob. 103CRCh. 3 - Prob. 104CRCh. 3 - Prob. 105CRCh. 3 - Prob. 106CRCh. 3 - Prob. 107CRCh. 3 - Prob. 108CRCh. 3 - Prob. 109CRCh. 3 - Prob. 110CRCh. 3 - Prob. 111CRCh. 3 - Prob. 112CRCh. 3 - Prob. 113CRCh. 3 - Prob. 114CRCh. 3 - Prob. 115CRCh. 3 - Prob. 116CRCh. 3 - Prob. 117CRCh. 3 - Prob. 118CRCh. 3 - Prob. 119CRCh. 3 - Prob. 120CRCh. 3 - Prob. 121CRCh. 3 - Prob. 122CRCh. 3 - Prob. 123CRCh. 3 - Prob. 124CRCh. 3 - Prob. 125CRCh. 3 - Prob. 126CRCh. 3 - Prob. 1CTCh. 3 - Prob. 2CTCh. 3 - Prob. 3CTCh. 3 - Prob. 4CTCh. 3 - Prob. 5CTCh. 3 - Prob. 6CTCh. 3 - Prob. 7CTCh. 3 - Prob. 8CTCh. 3 - Prob. 9CTCh. 3 - Prob. 10CTCh. 3 - Prob. 11CTCh. 3 - Prob. 12CTCh. 3 - Prob. 13CTCh. 3 - Prob. 14CTCh. 3 - Prob. 15CTCh. 3 - Prob. 16CTCh. 3 - Prob. 17CTCh. 3 - Prob. 18CTCh. 3 - Prob. 19CTCh. 3 - Prob. 20CTCh. 3 - Prob. 21CTCh. 3 - Prob. 22CTCh. 3 - Prob. 23CTCh. 3 - Prob. 24CTCh. 3 - Prob. 25CTCh. 3 - Prob. 26CTCh. 3 - Prob. 27CTCh. 3 - Prob. 28CTCh. 3 - Prob. 29CTCh. 3 - Prob. 30CTCh. 3 - Prob. 1STPCh. 3 - Prob. 2STPCh. 3 - Prob. 3STPCh. 3 - Prob. 4STPCh. 3 - Prob. 5STPCh. 3 - Prob. 6STPCh. 3 - Prob. 7STPCh. 3 - Prob. 8STPCh. 3 - Prob. 9STPCh. 3 - Prob. 10STPCh. 3 - Prob. 11STPCh. 3 - Prob. 12STPCh. 3 - Prob. 13STPCh. 3 - Prob. 14STPCh. 3 - Prob. 15STPCh. 3 - Prob. 16STPCh. 3 - Prob. 17STPCh. 3 - Prob. 18STPCh. 3 - Prob. 19STPCh. 3 - Prob. 20STPCh. 3 - Prob. 21STPCh. 3 - Prob. 22STPCh. 3 - Prob. 23STPCh. 3 - Prob. 24STPCh. 3 - Prob. 25STPCh. 3 - Prob. 26STP
Knowledge Booster
Background pattern image
Calculus
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.
Similar questions
SEE MORE QUESTIONS
Recommended textbooks for you
Text book image
Calculus: Early Transcendentals
Calculus
ISBN:9781285741550
Author:James Stewart
Publisher:Cengage Learning
Text book image
Thomas' Calculus (14th Edition)
Calculus
ISBN:9780134438986
Author:Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:PEARSON
Text book image
Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:9780134763644
Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:PEARSON
Text book image
Calculus: Early Transcendentals
Calculus
ISBN:9781319050740
Author:Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:W. H. Freeman
Text book image
Precalculus
Calculus
ISBN:9780135189405
Author:Michael Sullivan
Publisher:PEARSON
Text book image
Calculus: Early Transcendental Functions
Calculus
ISBN:9781337552516
Author:Ron Larson, Bruce H. Edwards
Publisher:Cengage Learning
SEE MORE TEXTBOOKS
Finding Local Maxima and Minima by Differentiation; Author: Professor Dave Explains;https://www.youtube.com/watch?v=pvLj1s7SOtk;License: Standard YouTube License, CC-BY