Finite Mathematics (11th Edition)
11th Edition
ISBN: 9780321979438
Author: Margaret L. Lial, Raymond N. Greenwell, Nathan P. Ritchey
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 3.2, Problem 3E
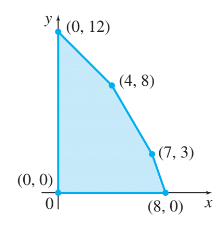
The following graphs show regions of feasible solutions. Use these regions to find maximum and minimum values of the given objective functions.
(a) z=5x+ 3y
(b) z = 1.50x + 0.25y
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
For context, the images attached below are a question from a June, 2024 past paper in statistical modeling
For context, the images attached below (question and related graph) are from a February 2024 past paper in statistical modeling
For context, the images attached below are from a February 2024 past paper in statistical modeling
Chapter 3 Solutions
Finite Mathematics (11th Edition)
Ch. 3.1 - Graph each linear inequality. x + y 2Ch. 3.1 - Graph each linear inequality. y x + 1Ch. 3.1 - Graph each linear inequality. x 2 yCh. 3.1 - Graph each linear inequality. y x 3Ch. 3.1 - Graph each linear inequality. 4x y 6Ch. 3.1 - Graph each linear inequality. 4y + x 6Ch. 3.1 - Graph each linear inequality. 7. 4x + y 8Ch. 3.1 - Graph each linear inequality. 2x y 2Ch. 3.1 - Graph each linear inequality. x + 3y 2Ch. 3.1 - Graph each linear inequality. 2x + 3y 6
Ch. 3.1 - Graph each linear inequality. x 3yCh. 3.1 - Graph each linear inequality. 2x yCh. 3.1 - Graph each linear inequality. x + y 0Ch. 3.1 - Graph each linear inequality. 3x + 2y 0Ch. 3.1 - Graph each linear inequality. y xCh. 3.1 - Graph each linear inequality. y 5xCh. 3.1 - Graph each linear inequality. x 4Ch. 3.1 - Graph each linear inequality. y 5Ch. 3.1 - Graph each linear inequality. y 2Ch. 3.1 - Graph each linear inequality. x 4Ch. 3.1 - Graph the feasible region for each system of...Ch. 3.1 - Graph the feasible region for each system of...Ch. 3.1 - Graph the feasible region for each system of...Ch. 3.1 - Graph the feasible region for each system of...Ch. 3.1 - Graph the feasible region for each system of...Ch. 3.1 - Graph the feasible region for each system of...Ch. 3.1 - Graph the feasible region for each system of...Ch. 3.1 - Graph the feasible region for each system of...Ch. 3.1 - Graph the feasible region for each system of...Ch. 3.1 - Graph the feasible region for each system of...Ch. 3.1 - Graph the feasible region for each system of...Ch. 3.1 - Graph the feasible region for each system of...Ch. 3.1 - Graph the feasible region for each system of...Ch. 3.1 - Graph the feasible region for each system of...Ch. 3.1 - Prob. 35ECh. 3.1 - Prob. 36ECh. 3.1 - Prob. 37ECh. 3.1 - Prob. 38ECh. 3.1 - The regions A through G in the figure can be...Ch. 3.1 - Production Scheduling A small pottery shop makes...Ch. 3.1 - Time Management Carmella and Walt produce handmade...Ch. 3.1 - Prob. 42ECh. 3.1 - Prob. 43ECh. 3.1 - Prob. 44ECh. 3.1 - For Exercises 42-47, perform the following steps....Ch. 3.1 - Prob. 46ECh. 3.1 - Prob. 47ECh. 3.2 - The following graphs show regions of feasible...Ch. 3.2 - The following graphs show regions of feasible...Ch. 3.2 - The following graphs show regions of feasible...Ch. 3.2 - The following graphs show regions of feasible...Ch. 3.2 - The following graphs show regions of feasible...Ch. 3.2 - Prob. 6ECh. 3.2 - Prob. 7ECh. 3.2 - Use graphical methods to solve each linear...Ch. 3.2 - Prob. 9ECh. 3.2 - Use graphical methods to solve each linear...Ch. 3.2 - Prob. 11ECh. 3.2 - Prob. 12ECh. 3.2 - Prob. 13ECh. 3.2 - Prob. 14ECh. 3.2 - Prob. 15ECh. 3.2 - Use graphical methods to solve each linear...Ch. 3.2 - Use graphical methods to solve each linear...Ch. 3.3 - Write Exercises 16 as linear inequalities....Ch. 3.3 - Prob. 2ECh. 3.3 - Prob. 3ECh. 3.3 - Prob. 4ECh. 3.3 - Prob. 5ECh. 3.3 - Prob. 6ECh. 3.3 - Transportation The Miers Company produces small...Ch. 3.3 - Transportation A manufacturer of refrigerators...Ch. 3.3 - Finance A pension fund manager decides to invest a...Ch. 3.3 - Profit A small country can grow only two crops for...Ch. 3.3 - Prob. 11ECh. 3.3 - Revenue A candy company has 150 kg of...Ch. 3.3 - Blending The Mostpure Milk Company gets milk from...Ch. 3.3 - Profit The Muro Manufacturing Company makes two...Ch. 3.3 - Prob. 15ECh. 3.3 - Revenue The manufacturing process requires that...Ch. 3.3 - Prob. 17ECh. 3.3 - Manufacturing (Note: Exercises #x2013;20 are from...Ch. 3.3 - Prob. 19ECh. 3.3 - Prob. 20ECh. 3.3 - Life Sciences Health Care David Willis takes...Ch. 3.3 - Prob. 22ECh. 3.3 - Nutrition A dietician is planning a snack package...Ch. 3.3 - Prob. 24ECh. 3.3 - Anthropology An anthropology article presents a...Ch. 3.3 - Prob. 26ECh. 3.3 - Prob. 27ECh. 3 - Use sensitivity analysis to find the optimal...Ch. 3 - Prob. 2EACh. 3 - Prob. 3EACh. 3 - Prob. 4EACh. 3 - Prob. 5EACh. 3 - Prob. 1RECh. 3 - Prob. 2RECh. 3 - Prob. 3RECh. 3 - Prob. 4RECh. 3 - Prob. 5RECh. 3 - Prob. 6RECh. 3 - Prob. 7RECh. 3 - Prob. 8RECh. 3 - Prob. 9RECh. 3 - Prob. 10RECh. 3 - Prob. 11RECh. 3 - Prob. 12RECh. 3 - Prob. 13RECh. 3 - How many constraints are we limited to in the...Ch. 3 - Prob. 15RECh. 3 - Prob. 16RECh. 3 - Prob. 17RECh. 3 - Prob. 18RECh. 3 - Prob. 19RECh. 3 - Prob. 20RECh. 3 - Prob. 21RECh. 3 - Prob. 22RECh. 3 - Prob. 23RECh. 3 - Prob. 24RECh. 3 - Prob. 25RECh. 3 - Prob. 26RECh. 3 - Prob. 27RECh. 3 - Use the given regions to find the maximum and...Ch. 3 - Prob. 29RECh. 3 - Prob. 30RECh. 3 - Prob. 31RECh. 3 - Prob. 32RECh. 3 - Prob. 33RECh. 3 - Prob. 34RECh. 3 - Prob. 35RECh. 3 - Prob. 36RECh. 3 - Prob. 37RECh. 3 - Cost Analysis DeMarco's pizza shop makes two...Ch. 3 - Prob. 39RECh. 3 - Revenue How many pizzas of each kind should the...Ch. 3 - Prob. 41RECh. 3 - Prob. 42RECh. 3 - Steel A steel company produces two types of...Ch. 3 - Prob. 44RECh. 3 - Prob. 45RECh. 3 - Prob. 46RE
Additional Math Textbook Solutions
Find more solutions based on key concepts
1. How much money is Joe earning when he’s 30?
Pathways To Math Literacy (looseleaf)
23. A plant nursery sells two sizes of oak trees to landscapers. Large trees cost the nursery $120 from the gro...
College Algebra (Collegiate Math)
True or False The quotient of two polynomial expressions is a rational expression, (p. A35)
Precalculus
Provide an example of a qualitative variable and an example of a quantitative variable.
Elementary Statistics ( 3rd International Edition ) Isbn:9781260092561
153. A rain gutter is made from sheets of aluminum that are 20 inches wide. As shown in the figure, the edges ...
College Algebra (7th Edition)
Find E(X) for each of the distributions given in Exercise 2.1-3.
Probability And Statistical Inference (10th Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.Similar questions
- For context, the image provided below is a question from a September, 2024 past paper in statistical modelingarrow_forwardFor context, the image below is from a January 2024 past paper in statistical modelingarrow_forwardFor context, the image provided below is a question from a September, 2024 past paper in statistical modelingarrow_forward
- If u use any type of chatgpt, will.downvote.arrow_forwardA function is defined on the interval (-π/2,π/2) by this multipart rule: if -π/2 < x < 0 f(x) = a if x=0 31-tan x +31-cot x if 0 < x < π/2 Here, a and b are constants. Find a and b so that the function f(x) is continuous at x=0. a= b= 3arrow_forwardUse the definition of continuity and the properties of limits to show that the function is continuous at the given number a. f(x) = (x + 4x4) 5, a = -1 lim f(x) X--1 = lim x+4x X--1 lim X-1 4 x+4x 5 ))" 5 )) by the power law by the sum law lim (x) + lim X--1 4 4x X-1 -(0,00+( Find f(-1). f(-1)=243 lim (x) + -1 +4 35 4 ([ ) lim (x4) 5 x-1 Thus, by the definition of continuity, f is continuous at a = -1. by the multiple constant law by the direct substitution propertyarrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Algebra for College StudentsAlgebraISBN:9781285195780Author:Jerome E. Kaufmann, Karen L. SchwittersPublisher:Cengage Learning
Elementary Linear Algebra (MindTap Course List)AlgebraISBN:9781305658004Author:Ron LarsonPublisher:Cengage Learning
College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell
Glencoe Algebra 1, Student Edition, 9780079039897...
Algebra
ISBN:9780079039897
Author:Carter
Publisher:McGraw Hill
Algebra for College Students
Algebra
ISBN:9781285195780
Author:Jerome E. Kaufmann, Karen L. Schwitters
Publisher:Cengage Learning
Elementary Linear Algebra (MindTap Course List)
Algebra
ISBN:9781305658004
Author:Ron Larson
Publisher:Cengage Learning
College Algebra (MindTap Course List)
Algebra
ISBN:9781305652231
Author:R. David Gustafson, Jeff Hughes
Publisher:Cengage Learning
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
Algebra: Structure And Method, Book 1
Algebra
ISBN:9780395977224
Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. Cole
Publisher:McDougal Littell
Solve ANY Optimization Problem in 5 Steps w/ Examples. What are they and How do you solve them?; Author: Ace Tutors;https://www.youtube.com/watch?v=BfOSKc_sncg;License: Standard YouTube License, CC-BY
Types of solution in LPP|Basic|Multiple solution|Unbounded|Infeasible|GTU|Special case of LP problem; Author: Mechanical Engineering Management;https://www.youtube.com/watch?v=F-D2WICq8Sk;License: Standard YouTube License, CC-BY
Optimization Problems in Calculus; Author: Professor Dave Explains;https://www.youtube.com/watch?v=q1U6AmIa_uQ;License: Standard YouTube License, CC-BY
Introduction to Optimization; Author: Math with Dr. Claire;https://www.youtube.com/watch?v=YLzgYm2tN8E;License: Standard YouTube License, CC-BY