Algebra 1
Algebra 1
1st Edition
ISBN: 9780078884801
Author: McGraw-Hill/Glencoe
Publisher: Glencoe/McGraw-Hill School Pub Co
bartleby

Concept explainers

Family of Curves
A family of curves is a group of curves that are each described by a parametrization in which one or more variables are parameters. In general, the parameters have more complexity on the assembly of the curve than an ordinary linear transformation. These…
XZ Plane
In order to understand XZ plane, it's helpful to understand two-dimensional and three-dimensional spaces. To plot a point on a plane, two numbers are needed, and these two numbers in the plane can be represented as an ordered pair (a,b) where a and b are…
Euclidean Geometry
Geometry is the branch of mathematics that deals with flat surfaces like lines, angles, points, two-dimensional figures, etc. In Euclidean geometry, one studies the geometrical shapes that rely on different theorems and axioms. This (pure mathematics) ge…
Lines and Angles
In a two-dimensional plane, a line is simply a figure that joins two points. Usually, lines are used for presenting objects that are straight in shape and have minimal depth or width.
bartleby

Videos

Question
Book Icon
Chapter 3.1, Problem 24PPS
To determine

Graph the equation by using x and y − intercept.

Expert Solution & Answer
Check Mark

Answer to Problem 24PPS

x and y intercepts are x= − 1.667 and y = 5

Explanation of Solution

Given:

The equation: 5−y=−3x

Concept Used:

The  x -intercepts are where the graph crosses the  x -axis, and the  y -intercepts are where the graph crosses the  y -axis.

Then, algebraically,

  • an  x -intercept is a point on the graph where  y  is zero, and
  • a  y -intercept is a point on the graph where  x  is zero.

More specifically,

  • an  x -intercept is a point in the equation where the  y -value is zero, and
  • a  y -intercept is a point in the equation where the  x -value is zero.

Calculation:

The equation: 5−y=−3x

Find the x − intercept, plug in y = 0 in the equation.

  5−y=−3x5−0=−3x    [  plug  in  y  =0  ]5=−3x  [ Subtract  2x  from  both  sides ]5−3  =  −3x−3   [  Divide  each  side  by  −2  ]x=−53  =   −   1.667x=−1.667 x − Intercept: x= − 1.667

Find the y − intercept, plug in x = 0 in the equation

  5−y=−3x5−y=−3  ·  0  [  plug  in  x  =0  ]5−y=05−5−y=−5  [ Subtract  5  from  both  sides ]−y=−5−y−1  =  −5−1   [  Divide  each  side  by  −1  ]y=5 y − Intercept: y = 5

Graph the line 5−y=−3x with x and y intercepts points are (− 1.667, 0) and (0, 5)

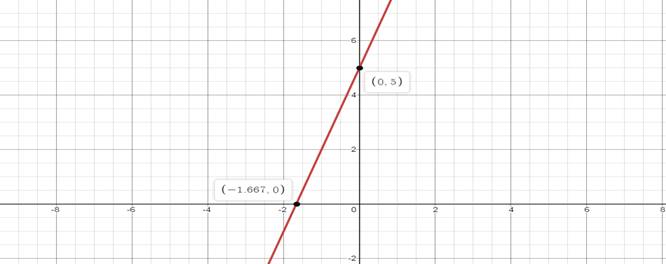
  Algebra 1, Chapter 3.1, Problem 24PPS

Thus, x and y intercepts are x = − 1.667 and y = 5

Previous
Chapter 3.1, Problem 23PPS
Next
Chapter 3.1, Problem 25PPS

Chapter 3 Solutions

Algebra 1

Ch. 3.1 - Prob. 35PPSCh. 3.1 - Prob. 58PPSCh. 3.1 - Prob. 60HPCh. 3.1 - Prob. 68STPCh. 3.1 - Prob. 1ACYPCh. 3.1 - Prob. 1BCYPCh. 3.1 - Prob. 2CYPCh. 3.1 - Prob. 3CYPCh. 3.1 - Prob. 4ACYPCh. 3.1 - Prob. 4BCYP
Ch. 3.1 - Prob. 5ACYPCh. 3.1 - Prob. 5BCYPCh. 3.1 - Prob. 5CCYPCh. 3.1 - Prob. 1CYUCh. 3.1 - Prob. 2CYUCh. 3.1 - Prob. 3CYUCh. 3.1 - Prob. 4CYUCh. 3.1 - Prob. 5CYUCh. 3.1 - Prob. 6CYUCh. 3.1 - Prob. 7CYUCh. 3.1 - Prob. 8CYUCh. 3.1 - Prob. 9CYUCh. 3.1 - Prob. 10CYUCh. 3.1 - Prob. 11CYUCh. 3.1 - Prob. 12CYUCh. 3.1 - Prob. 13PPSCh. 3.1 - Prob. 14PPSCh. 3.1 - Prob. 15PPSCh. 3.1 - Prob. 16PPSCh. 3.1 - Prob. 17PPSCh. 3.1 - Prob. 18PPSCh. 3.1 - Prob. 19PPSCh. 3.1 - Prob. 20PPSCh. 3.1 - Prob. 21PPSCh. 3.1 - Prob. 22PPSCh. 3.1 - Prob. 23PPSCh. 3.1 - Prob. 24PPSCh. 3.1 - Prob. 25PPSCh. 3.1 - Prob. 26PPSCh. 3.1 - Prob. 27PPSCh. 3.1 - Prob. 28PPSCh. 3.1 - Prob. 29PPSCh. 3.1 - Prob. 30PPSCh. 3.1 - Prob. 31PPSCh. 3.1 - Prob. 32PPSCh. 3.1 - Prob. 33PPSCh. 3.1 - Prob. 34PPSCh. 3.1 - Prob. 36PPSCh. 3.1 - Prob. 37PPSCh. 3.1 - Prob. 38PPSCh. 3.1 - Prob. 39PPSCh. 3.1 - Prob. 40PPSCh. 3.1 - Prob. 41PPSCh. 3.1 - Prob. 42PPSCh. 3.1 - Prob. 43PPSCh. 3.1 - Prob. 44PPSCh. 3.1 - Prob. 45PPSCh. 3.1 - Prob. 46PPSCh. 3.1 - Prob. 47PPSCh. 3.1 - Prob. 48PPSCh. 3.1 - Prob. 49PPSCh. 3.1 - Prob. 50PPSCh. 3.1 - Prob. 51PPSCh. 3.1 - Prob. 52PPSCh. 3.1 - Prob. 53PPSCh. 3.1 - Prob. 54PPSCh. 3.1 - Prob. 55PPSCh. 3.1 - Prob. 56PPSCh. 3.1 - Prob. 57PPSCh. 3.1 - Prob. 59HPCh. 3.1 - Prob. 61HPCh. 3.1 - Prob. 62HPCh. 3.1 - Prob. 63HPCh. 3.1 - Prob. 64HPCh. 3.1 - Prob. 65STPCh. 3.1 - Prob. 66STPCh. 3.1 - Prob. 67STPCh. 3.1 - Prob. 69SRCh. 3.1 - Prob. 70SRCh. 3.1 - Prob. 71SRCh. 3.1 - Prob. 72SRCh. 3.1 - Prob. 73SRCh. 3.1 - Prob. 74SCh. 3.1 - Prob. 75SCh. 3.1 - Prob. 76SCh. 3.1 - Prob. 77SCh. 3.2 - Prob. 3CYPCh. 3.2 - Prob. 9CYUCh. 3.2 - Prob. 22PPSCh. 3.2 - Prob. 23PPSCh. 3.2 - Prob. 37PPSCh. 3.2 - Prob. 44PPSCh. 3.2 - Prob. 45PPSCh. 3.2 - Prob. 53STPCh. 3.2 - Prob. 1ACYPCh. 3.2 - Prob. 1BCYPCh. 3.2 - Prob. 2ACYPCh. 3.2 - Prob. 2BCYPCh. 3.2 - Prob. 1CYUCh. 3.2 - Prob. 2CYUCh. 3.2 - Prob. 3CYUCh. 3.2 - Prob. 4CYUCh. 3.2 - Prob. 5CYUCh. 3.2 - Prob. 6CYUCh. 3.2 - Prob. 7CYUCh. 3.2 - Prob. 8CYUCh. 3.2 - Prob. 10PPSCh. 3.2 - Prob. 11PPSCh. 3.2 - Prob. 12PPSCh. 3.2 - Prob. 13PPSCh. 3.2 - Prob. 14PPSCh. 3.2 - Prob. 15PPSCh. 3.2 - Prob. 16PPSCh. 3.2 - Prob. 17PPSCh. 3.2 - Prob. 18PPSCh. 3.2 - Prob. 19PPSCh. 3.2 - Prob. 20PPSCh. 3.2 - Prob. 21PPSCh. 3.2 - Prob. 24PPSCh. 3.2 - Prob. 25PPSCh. 3.2 - Prob. 26PPSCh. 3.2 - Prob. 27PPSCh. 3.2 - Prob. 28PPSCh. 3.2 - Prob. 29PPSCh. 3.2 - Prob. 30PPSCh. 3.2 - Prob. 31PPSCh. 3.2 - Prob. 32PPSCh. 3.2 - Prob. 33PPSCh. 3.2 - Prob. 34PPSCh. 3.2 - Prob. 35PPSCh. 3.2 - Prob. 36PPSCh. 3.2 - Prob. 38PPSCh. 3.2 - Prob. 39PPSCh. 3.2 - Prob. 40PPSCh. 3.2 - Prob. 41PPSCh. 3.2 - Prob. 42PPSCh. 3.2 - Prob. 43PPSCh. 3.2 - Prob. 46HPCh. 3.2 - Prob. 47HPCh. 3.2 - Prob. 48HPCh. 3.2 - Prob. 49HPCh. 3.2 - Prob. 50HPCh. 3.2 - Prob. 51STPCh. 3.2 - Prob. 52STPCh. 3.2 - Prob. 54STPCh. 3.2 - Prob. 55SRCh. 3.2 - Prob. 56SRCh. 3.2 - Prob. 57SRCh. 3.2 - Prob. 58SRCh. 3.2 - Prob. 59SRCh. 3.2 - Prob. 60SRCh. 3.2 - Prob. 61SCh. 3.2 - Prob. 62SCh. 3.2 - Prob. 63SCh. 3.2 - Prob. 64SCh. 3.2 - Prob. 65SCh. 3.2 - Prob. 66SCh. 3.2 - Prob. 67SCh. 3.3 - Prob. 1ACYPCh. 3.3 - Prob. 1BCYPCh. 3.3 - Prob. 2CYPCh. 3.3 - Prob. 3ACYPCh. 3.3 - Prob. 3BCYPCh. 3.3 - Prob. 4ACYPCh. 3.3 - Prob. 4BCYPCh. 3.3 - Prob. 4CCYPCh. 3.3 - Prob. 4DCYPCh. 3.3 - Prob. 4ECYPCh. 3.3 - Prob. 4FCYPCh. 3.3 - Prob. 5ACYPCh. 3.3 - Prob. 5BCYPCh. 3.3 - Prob. 6ACYPCh. 3.3 - Prob. 6BCYPCh. 3.3 - Prob. 1CYUCh. 3.3 - Prob. 2CYUCh. 3.3 - Prob. 3CYUCh. 3.3 - Prob. 4CYUCh. 3.3 - Prob. 5CYUCh. 3.3 - Prob. 6CYUCh. 3.3 - Prob. 7CYUCh. 3.3 - Prob. 8CYUCh. 3.3 - Prob. 9CYUCh. 3.3 - Prob. 10CYUCh. 3.3 - Prob. 11CYUCh. 3.3 - Prob. 12CYUCh. 3.3 - Prob. 13CYUCh. 3.3 - Prob. 14PPSCh. 3.3 - Prob. 15PPSCh. 3.3 - Prob. 16PPSCh. 3.3 - Prob. 17PPSCh. 3.3 - Prob. 18PPSCh. 3.3 - Prob. 19PPSCh. 3.3 - Prob. 20PPSCh. 3.3 - Prob. 21PPSCh. 3.3 - Prob. 22PPSCh. 3.3 - Prob. 23PPSCh. 3.3 - Prob. 24PPSCh. 3.3 - Prob. 25PPSCh. 3.3 - Prob. 26PPSCh. 3.3 - Prob. 27PPSCh. 3.3 - Prob. 28PPSCh. 3.3 - Prob. 29PPSCh. 3.3 - Prob. 30PPSCh. 3.3 - Prob. 31PPSCh. 3.3 - Prob. 32PPSCh. 3.3 - Prob. 33PPSCh. 3.3 - Prob. 34PPSCh. 3.3 - Prob. 35PPSCh. 3.3 - Prob. 36PPSCh. 3.3 - Prob. 37PPSCh. 3.3 - Prob. 38PPSCh. 3.3 - Prob. 39PPSCh. 3.3 - Prob. 40PPSCh. 3.3 - Prob. 41PPSCh. 3.3 - Prob. 42PPSCh. 3.3 - Prob. 43PPSCh. 3.3 - Prob. 44PPSCh. 3.3 - Prob. 45PPSCh. 3.3 - Prob. 46PPSCh. 3.3 - Prob. 47PPSCh. 3.3 - Prob. 48HPCh. 3.3 - Prob. 49HPCh. 3.3 - Prob. 50HPCh. 3.3 - Prob. 51HPCh. 3.3 - Prob. 52HPCh. 3.3 - Prob. 53STPCh. 3.3 - Prob. 54STPCh. 3.3 - Prob. 55STPCh. 3.3 - Prob. 56STPCh. 3.3 - Prob. 57SRCh. 3.3 - Prob. 58SRCh. 3.3 - Prob. 59SRCh. 3.3 - Prob. 60SRCh. 3.3 - Prob. 61SRCh. 3.3 - Prob. 62SRCh. 3.3 - Prob. 63SCh. 3.3 - Prob. 64SCh. 3.3 - Prob. 65SCh. 3.3 - Prob. 66SCh. 3.3 - Prob. 67SCh. 3.3 - Prob. 68SCh. 3.4 - Prob. 1ACYPCh. 3.4 - Prob. 1BCYPCh. 3.4 - Prob. 2ACYPCh. 3.4 - Prob. 2BCYPCh. 3.4 - Prob. 2CCYPCh. 3.4 - Prob. 2DCYPCh. 3.4 - Prob. 3CYPCh. 3.4 - Prob. 4ACYPCh. 3.4 - Prob. 4BCYPCh. 3.4 - Prob. 4CCYPCh. 3.4 - Prob. 4DCYPCh. 3.4 - Prob. 1CYUCh. 3.4 - Prob. 2CYUCh. 3.4 - Prob. 3CYUCh. 3.4 - Prob. 4CYUCh. 3.4 - Prob. 5CYUCh. 3.4 - Prob. 6CYUCh. 3.4 - Prob. 7CYUCh. 3.4 - Prob. 8CYUCh. 3.4 - Prob. 9CYUCh. 3.4 - Prob. 10PPSCh. 3.4 - Prob. 11PPSCh. 3.4 - Prob. 12PPSCh. 3.4 - Prob. 13PPSCh. 3.4 - Prob. 14PPSCh. 3.4 - Prob. 15PPSCh. 3.4 - Prob. 16PPSCh. 3.4 - Prob. 17PPSCh. 3.4 - Prob. 18PPSCh. 3.4 - Prob. 19PPSCh. 3.4 - Prob. 20PPSCh. 3.4 - Prob. 21PPSCh. 3.4 - Prob. 22PPSCh. 3.4 - Prob. 23PPSCh. 3.4 - Prob. 24PPSCh. 3.4 - Prob. 25PPSCh. 3.4 - Prob. 26PPSCh. 3.4 - Prob. 27PPSCh. 3.4 - Prob. 28PPSCh. 3.4 - Prob. 29PPSCh. 3.4 - Prob. 30PPSCh. 3.4 - Prob. 31PPSCh. 3.4 - Prob. 32PPSCh. 3.4 - Prob. 33PPSCh. 3.4 - Prob. 34PPSCh. 3.4 - Prob. 35PPSCh. 3.4 - Prob. 36PPSCh. 3.4 - Prob. 37PPSCh. 3.4 - Prob. 38PPSCh. 3.4 - Prob. 39PPSCh. 3.4 - Prob. 40PPSCh. 3.4 - Prob. 41PPSCh. 3.4 - Prob. 42PPSCh. 3.4 - Prob. 43PPSCh. 3.4 - Prob. 44PPSCh. 3.4 - Prob. 45HPCh. 3.4 - Prob. 46HPCh. 3.4 - Prob. 47HPCh. 3.4 - Prob. 48HPCh. 3.4 - Prob. 49HPCh. 3.4 - Prob. 50HPCh. 3.4 - Prob. 51STPCh. 3.4 - Prob. 52STPCh. 3.4 - Prob. 53STPCh. 3.4 - Prob. 54STPCh. 3.4 - Prob. 55SRCh. 3.4 - Prob. 56SRCh. 3.4 - Prob. 57SRCh. 3.4 - Prob. 58SRCh. 3.4 - Prob. 59SRCh. 3.4 - Prob. 60SRCh. 3.4 - Prob. 61SRCh. 3.4 - Prob. 62SRCh. 3.4 - Prob. 63SRCh. 3.4 - Prob. 64SRCh. 3.4 - Prob. 65SRCh. 3.4 - Prob. 66SRCh. 3.4 - Prob. 67SRCh. 3.4 - Prob. 68SCh. 3.4 - Prob. 69SCh. 3.4 - Prob. 70SCh. 3.4 - Prob. 71SCh. 3.4 - Prob. 72SCh. 3.4 - Prob. 73SCh. 3.5 - Prob. 1ACYPCh. 3.5 - Prob. 1BCYPCh. 3.5 - Prob. 2CYPCh. 3.5 - Prob. 3ACYPCh. 3.5 - Prob. 3BCYPCh. 3.5 - Prob. 3CCYPCh. 3.5 - Prob. 3DCYPCh. 3.5 - Prob. 4ACYPCh. 3.5 - Prob. 4BCYPCh. 3.5 - Prob. 1CYUCh. 3.5 - Prob. 2CYUCh. 3.5 - Prob. 3CYUCh. 3.5 - Prob. 4CYUCh. 3.5 - Prob. 5CYUCh. 3.5 - Prob. 6CYUCh. 3.5 - Prob. 7CYUCh. 3.5 - Prob. 8PPSCh. 3.5 - Prob. 9PPSCh. 3.5 - Prob. 10PPSCh. 3.5 - Prob. 11PPSCh. 3.5 - Prob. 12PPSCh. 3.5 - Prob. 13PPSCh. 3.5 - Prob. 14PPSCh. 3.5 - Prob. 15PPSCh. 3.5 - Prob. 16PPSCh. 3.5 - Prob. 17PPSCh. 3.5 - Prob. 18PPSCh. 3.5 - Prob. 19PPSCh. 3.5 - Prob. 20PPSCh. 3.5 - Prob. 21PPSCh. 3.5 - Prob. 22PPSCh. 3.5 - Prob. 23PPSCh. 3.5 - Prob. 24PPSCh. 3.5 - Prob. 25PPSCh. 3.5 - Prob. 26PPSCh. 3.5 - Prob. 27PPSCh. 3.5 - Prob. 28PPSCh. 3.5 - Prob. 29PPSCh. 3.5 - Prob. 30PPSCh. 3.5 - Prob. 32HPCh. 3.5 - Prob. 33HPCh. 3.5 - Prob. 34HPCh. 3.5 - Prob. 35HPCh. 3.5 - Prob. 36HPCh. 3.5 - Prob. 37STPCh. 3.5 - Prob. 38STPCh. 3.5 - Prob. 39STPCh. 3.5 - Prob. 40STPCh. 3.5 - Prob. 41SRCh. 3.5 - Prob. 42SRCh. 3.5 - Prob. 43SRCh. 3.5 - Prob. 44SRCh. 3.5 - Prob. 45SRCh. 3.5 - Prob. 46SRCh. 3.5 - Prob. 47SRCh. 3.5 - Prob. 48SRCh. 3.5 - Prob. 49SRCh. 3.5 - Prob. 50SCh. 3.5 - Prob. 51SCh. 3.5 - Prob. 52SCh. 3.5 - Prob. 53SCh. 3.5 - Prob. 54SCh. 3.5 - Prob. 55SCh. 3.5 - Prob. 31PPSCh. 3.6 - Prob. 2CYUCh. 3.6 - Prob. 3CYUCh. 3.6 - Prob. 5PPSCh. 3.6 - Prob. 6PPSCh. 3.6 - Prob. 7PPSCh. 3.6 - Prob. 8PPSCh. 3.6 - Prob. 9PPSCh. 3.6 - Prob. 10PPSCh. 3.6 - Prob. 1CYUCh. 3.6 - Prob. 4PPSCh. 3.6 - Prob. 11PPSCh. 3.6 - Prob. 12PPSCh. 3.6 - Prob. 13PPSCh. 3.6 - Prob. 14HPCh. 3.6 - Prob. 15HPCh. 3.6 - Prob. 16HPCh. 3.6 - Prob. 17HPCh. 3.6 - Prob. 18HPCh. 3.6 - Prob. 1ACYPCh. 3.6 - Prob. 1BCYPCh. 3.6 - Prob. 1CCYPCh. 3.6 - Prob. 2ACYPCh. 3.6 - Prob. 2BCYPCh. 3.6 - Prob. 19STPCh. 3.6 - Prob. 20STPCh. 3.6 - Prob. 21STPCh. 3.6 - Prob. 22STPCh. 3.6 - Prob. 23SRCh. 3.6 - Prob. 24SRCh. 3.6 - Prob. 25SRCh. 3.6 - Prob. 26SRCh. 3.6 - Prob. 27SRCh. 3.6 - Prob. 28SRCh. 3.6 - Prob. 29SRCh. 3.6 - Prob. 30SCh. 3.6 - Prob. 31SCh. 3.6 - Prob. 32SCh. 3.6 - Prob. 33SCh. 3.6 - Prob. 34SCh. 3.6 - Prob. 35SCh. 3 - Prob. 1QCCh. 3 - Prob. 2QCCh. 3 - Prob. 3QCCh. 3 - Prob. 4QCCh. 3 - Prob. 5QCCh. 3 - Prob. 6QCCh. 3 - Prob. 13QCCh. 3 - Prob. 14QCCh. 3 - Prob. 15QCCh. 3 - Prob. 16QCCh. 3 - Prob. 17QCCh. 3 - Prob. 18QCCh. 3 - Prob. 19QCCh. 3 - Prob. 20QCCh. 3 - Prob. 21QCCh. 3 - Prob. 22QCCh. 3 - Prob. 23QCCh. 3 - Prob. 1MCQCh. 3 - Prob. 2MCQCh. 3 - Prob. 3MCQCh. 3 - Prob. 4MCQCh. 3 - Prob. 5MCQCh. 3 - Prob. 6MCQCh. 3 - Prob. 9MCQCh. 3 - Prob. 10MCQCh. 3 - Prob. 11MCQCh. 3 - Prob. 12MCQCh. 3 - Prob. 13MCQCh. 3 - Prob. 14MCQCh. 3 - Prob. 15MCQCh. 3 - Prob. 16MCQCh. 3 - Prob. 17MCQCh. 3 - Prob. 18MCQCh. 3 - Prob. 19MCQCh. 3 - Prob. 20MCQCh. 3 - Prob. 21MCQCh. 3 - Prob. 22MCQCh. 3 - Prob. 23MCQCh. 3 - Prob. 24MCQCh. 3 - Prob. 1SGRCh. 3 - Prob. 2SGRCh. 3 - Prob. 3SGRCh. 3 - Prob. 4SGRCh. 3 - Prob. 5SGRCh. 3 - Prob. 6SGRCh. 3 - Prob. 13SGRCh. 3 - Prob. 14SGRCh. 3 - Prob. 15SGRCh. 3 - Prob. 16SGRCh. 3 - Prob. 17SGRCh. 3 - Prob. 18SGRCh. 3 - Prob. 19SGRCh. 3 - Prob. 20SGRCh. 3 - Prob. 21SGRCh. 3 - Prob. 22SGRCh. 3 - Prob. 23SGRCh. 3 - Prob. 24SGRCh. 3 - Prob. 25SGRCh. 3 - Prob. 26SGRCh. 3 - Prob. 27SGRCh. 3 - Prob. 28SGRCh. 3 - Prob. 29SGRCh. 3 - Prob. 30SGRCh. 3 - Prob. 31SGRCh. 3 - Prob. 32SGRCh. 3 - Prob. 33SGRCh. 3 - Prob. 34SGRCh. 3 - Prob. 35SGRCh. 3 - Prob. 36SGRCh. 3 - Prob. 37SGRCh. 3 - Prob. 38SGRCh. 3 - Prob. 39SGRCh. 3 - Prob. 40SGRCh. 3 - Prob. 41SGRCh. 3 - Prob. 42SGRCh. 3 - Prob. 43SGRCh. 3 - Prob. 44SGRCh. 3 - Prob. 45SGRCh. 3 - Prob. 2PTCh. 3 - Prob. 3PTCh. 3 - Prob. 4PTCh. 3 - Prob. 5PTCh. 3 - Prob. 6PTCh. 3 - Prob. 10PTCh. 3 - Prob. 11PTCh. 3 - Prob. 12PTCh. 3 - Prob. 13PTCh. 3 - Prob. 14PTCh. 3 - Prob. 15PTCh. 3 - Prob. 16PTCh. 3 - Prob. 17PTCh. 3 - Prob. 18PTCh. 3 - Prob. 19PTCh. 3 - Prob. 20PTCh. 3 - Prob. 21PTCh. 3 - Prob. 22PTCh. 3 - Prob. 23PTCh. 3 - Prob. 24PTCh. 3 - Prob. 25PTCh. 3 - Prob. 1STPCh. 3 - Prob. 2STPCh. 3 - Prob. 3STPCh. 3 - Prob. 4STPCh. 3 - Prob. 5STPCh. 3 - Prob. 6STPCh. 3 - Prob. 13STPCh. 3 - Prob. 14STPCh. 3 - Prob. 15STPCh. 3 - Prob. 16STPCh. 3 - Prob. 7QCCh. 3 - Prob. 8QCCh. 3 - Prob. 9QCCh. 3 - Prob. 10QCCh. 3 - Prob. 11QCCh. 3 - Prob. 12QCCh. 3 - Prob. 7MCQCh. 3 - Prob. 8MCQCh. 3 - Prob. 7SGRCh. 3 - Prob. 8SGRCh. 3 - Prob. 9SGRCh. 3 - Prob. 10SGRCh. 3 - Prob. 11SGRCh. 3 - Prob. 12SGRCh. 3 - Prob. 1PTCh. 3 - Prob. 7PTCh. 3 - Prob. 8PTCh. 3 - Prob. 9PTCh. 3 - Prob. 7STPCh. 3 - Prob. 8STPCh. 3 - Prob. 9STPCh. 3 - Prob. 10STPCh. 3 - Prob. 11STPCh. 3 - Prob. 12STP

Additional Math Textbook Solutions

Find more solutions based on key concepts
In Problems 13-24, determine whether the graph is that of a function by using the vertical-line test. If it is,...

Precalculus

Optimal garden A rectangular flower garden with an area of 30 m2 is surrounded by a grass border 1 m wide on tw...

Calculus: Early Transcendentals (2nd Edition)

31. Durations of Pregnancies The lengths of pregnancies are normally distributed with a mean of 268 days and a ...

Elementary Statistics (13th Edition)

Retirement Income Several times during the year, the U.S. Census Bureau takes random samples from the populatio...

Introductory Statistics

TRY IT YOURSELF 1 Find the mean of the points scored by the 51 winning teams listed on page 39.

Elementary Statistics: Picturing the World (7th Edition)

Solving Trigonometric Equations For Exercise 51–54, solve for the angle , where 51.

University Calculus: Early Transcendentals (4th Edition)

Knowledge Booster
Background pattern image
Algebra
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, algebra and related others by exploring similar questions and additional content below.
Similar questions
SEE MORE QUESTIONS
Recommended textbooks for you
Text book image
Algebra and Trigonometry (6th Edition)
Algebra
ISBN:9780134463216
Author:Robert F. Blitzer
Publisher:PEARSON
Text book image
Contemporary Abstract Algebra
Algebra
ISBN:9781305657960
Author:Joseph Gallian
Publisher:Cengage Learning
Text book image
Linear Algebra: A Modern Introduction
Algebra
ISBN:9781285463247
Author:David Poole
Publisher:Cengage Learning
Text book image
Algebra And Trigonometry (11th Edition)
Algebra
ISBN:9780135163078
Author:Michael Sullivan
Publisher:PEARSON
Text book image
Introduction to Linear Algebra, Fifth Edition
Algebra
ISBN:9780980232776
Author:Gilbert Strang
Publisher:Wellesley-Cambridge Press
Text book image
College Algebra (Collegiate Math)
Algebra
ISBN:9780077836344
Author:Julie Miller, Donna Gerken
Publisher:McGraw-Hill Education
SEE MORE TEXTBOOKS
Points, Lines, Planes, Segments, & Rays - Collinear vs Coplanar Points - Geometry; Author: The Organic Chemistry Tutor;https://www.youtube.com/watch?v=dDWjhRfBsKM;License: Standard YouTube License, CC-BY
Naming Points, Lines, and Planes; Author: Florida PASS Program;https://www.youtube.com/watch?v=F-LxiLSSaLg;License: Standard YouTube License, CC-BY