
Concept explainers
The estimated times and immediate predecessors for the activities in a project at George Kyparis’s retinal scanning company are given in the following table. Assume that the activity times are independent.
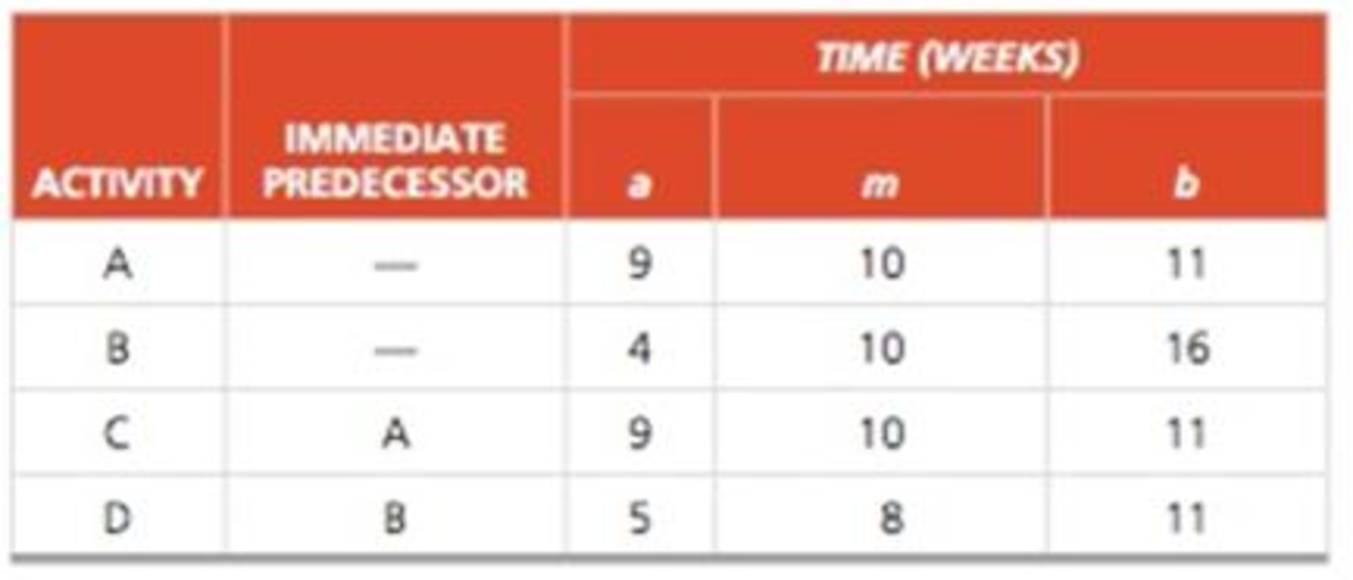
a) Calculate the expected time and variance for each activity.
b) What is the expected completion time of the critical path? What is the expected completion time of the other path in the network?
c) What is the variance of the critical path? What is the variance of the other path in the network?
d) If the time to complete path A–C is
e) If the time to complete path B–D is normally distributed, what is the probability that this path will be finished in 22 weeks or less?
f) Explain why the probability that the critical path will be finished in 22 weeks or less is not necessarily the probability that the project will be finished in 22 weeks or less.
a)
To determine: The expected time and variance.
Introduction:
The activity times of various tasks in a PERT project network are assumed to follow a probability distribution. For calculating the expected times and standard deviation, the parameters required are the following:
- Optimistic time: This is the time denoted by “a”, which is the best possible or in other words, the quickest time in which an activity can be completed, assuming that everything goes as per plan.
- Pessimistic time: This is the worst case scenario, where all the conditions are adverse or unfavorable. The maximum time which may be taken in such a situation is the pessimistic time denoted by “b”.
- Most likely time: The most realistic estimate of the time, denoted by “m” in normal conditions, is another parameter which is important in the computation of expected times and variances.
Answer to Problem 20P
The expected times and varianceare shown in Table 1.
Explanation of Solution
Given information:
| Activity | Immediate predecessor | Time in weeks | ||
| a | m | b | ||
| A | 9 | 10 | 11 | |
| B | 4 | 10 | 16 | |
| C | A | 9 | 10 | 11 |
| D | B | 5 | 8 | 11 |
Formula:
Calculate the expected time t and the variances for each activity by using the equations
where ‘a’ is the optimistic time, ‘m’ is the most likely time and ‘b’ is the most pessimistic time.
Calculation of expected time and variance:
The calculations are shown below.
| Activity | Immediate predecessor | Time in weeks | t | Variance | ||
| a | m | b | ||||
| A | 9 | 10 | 11 | 10 | 0.11 | |
| B | 4 | 10 | 16 | 10 | 4 | |
| C | A | 9 | 10 | 11 | 10 | 0.11 |
| D | B | 5 | 8 | 11 | 8 | 1 |
Table 1
Excel worksheet:

Hence, the expected times and variance are shown in Table 1.
b)
To determine: The expected completion of critical path and other path (non-ciritical paths).
Answer to Problem 20P
The critical path is AàC and its expected completion time is 20 weeks. The expected completion time of the other path BàD is 18 weeks.
Explanation of Solution
Given information:
| Activity | Immediate predecessor | Time in weeks | ||
| a | m | b | ||
| A | 9 | 10 | 11 | |
| B | 4 | 10 | 16 | |
| C | A | 9 | 10 | 11 |
| D | B | 5 | 8 | 11 |
Calculation of expected completion of critical path and other path (non-ciritical paths):
AON diagram is constructed which is shown below.
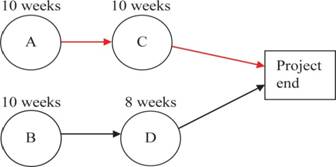
The critical path is AàC and expected completion time is 20 weeks. The expected completion time of the other path BàD is 18 weeks.
Hence, the critical path is AàC and its expected completion time is 20 weeks. The expected completion time of the other path BàD is 18 weeks.
c)
To determine: The variance of critical path and other path (non-ciritical paths).
Answer to Problem 20P
The variance of the critical path AàC is 0.222 weeks and other path BàD is5 weeks.
Explanation of Solution
Given information:
| Activity | Immediate predecessor | Time in weeks | ||
| a | m | b | ||
| A | 9 | 10 | 11 | |
| B | 4 | 10 | 16 | |
| C | A | 9 | 10 | 11 |
| D | B | 5 | 8 | 11 |
Calculation of variance of critical path and other path:
The variance of the critical path AàC is the sum of the variances of activities A and C.
The variance of the critical path is the sum of 0.1111 and 0.1111 (refer table 1) which is 0.2222 weeks.
The variance of the other path BàD is the sum of the variances of activities B and D.
The variance of the other path is the sum of 4 and 1 (refer table 1) which is 5 weeksThe variance of the other path BàD is 5 weeks.
Hence, the variance of the critical path AàC is 0.222 weeks and other path BàD is 5 weeks.
d)
To determine: The probability of finishing the project in 22 weeks, when A-C is normally distributed.
Answer to Problem 20P
Probability of finishing the project in 22 weeks is almost 1.
Explanation of Solution
Given information:
| Activity | Immediate predecessor | Time in weeks | ||
| a | m | b | ||
| A | 9 | 10 | 11 | |
| B | 4 | 10 | 16 | |
| C | A | 9 | 10 | 11 |
| D | B | 5 | 8 | 11 |
Probability of finishing the project in 22 weeks, when A-C is normally distributed:
The expected completion time of critical path AàC is 20 weeks with a variance of 0.22 weeks.
The standard deviation:
The standard deviation is calculated by taking square root of the variance which is 0.22 which yields 0.469.
Z value is calculated by dividing the difference of 22 and 20 with 0.469 which yields 4.264.
Reading from normal distribution tables given the mean is 20 weeks, the variance
Hence, probability of finishing the project in 22 weeks is almost 1.
e)
To determine: The probability of finishing the project in 22 weeks, when B-D is normally distributed.
Answer to Problem 20P
Probability of finishing the project in 22 weeks is 0.963.
Explanation of Solution
Given information:
| Activity | Immediate predecessor | Time in weeks | ||
| a | m | b | ||
| A | 9 | 10 | 11 | |
| B | 4 | 10 | 16 | |
| C | A | 9 | 10 | 11 |
| D | B | 5 | 8 | 11 |
Probability of finishing the project in 22 weeks, when B-D is normally distributed:
The expected completion time of path BàD is 18 weeks with a variance of 5 weeks.
The standard deviation:
The standard deviation is calculated by taking square root of the variance which is 5 which yields 2.236.
Z value is calculated by dividing the difference of 22 and 18 with 2.236 which yields 1.79.
Reading from normal distribution tables given the mean is 18 weeks, the variance
Hence, the probability of finishing the project in 22 weeks is 0.963.
f)
To explain: The reason for the probability that the critical path will be finished in 22 weeks or less is not necessarily the probability that the project will be finished in 22 weeks or less.
Explanation of Solution
Given information:
| Activity | Immediate predecessor | Time in weeks | ||
| a | m | b | ||
| A | 9 | 10 | 11 | |
| B | 4 | 10 | 16 | |
| C | A | 9 | 10 | 11 |
| D | B | 5 | 8 | 11 |
Explanation for the reason for the probability that the critical path will be finished in 22 weeks or less is not necessarily the probability that the project will be finished in 22 weeks or less:
The critical path AàC has a very small variance of only 0.22 weeks compared to the variance along path BàD which is 5 weeks. That is why, despite having lower expected time of completion of 18 weeks, the probability that the path BàD would be completed in 22 weeks is0.963.and is lower than the probability
The project is completed only when all the activities are completed.
Despite the probability of the critical path AàC, being completed in 22 weeks being almost 1, the probability that the project is completed in 22 weeks is0.963.
Want to see more full solutions like this?
Chapter 3 Solutions
Pearson eText Principles of Operations Management: Sustainability and Supply Chain Management -- Instant Access (Pearson+)
- IM.84 An outdoor equipment manufacturer sells a rugged water bottle to complement its product line. They sell this item to a variety of sporting goods stores and other retailers. The manufacturer offers quantity discounts per the following discount schedule: Option Plan Quantity Price A 1 - 2,399 $5.50 B 2,400 - 3,999 $5.20 C 4,000+ $4.50 A large big-box retailer expects to sell 9,700 units this year. This retailer estimates that it incurs an internal administrative cost of $225 each time it places an order with the manufacturer. Holding cost for the retailer is $55 per case per year. (There are 40 units or water bottles per case.) Based on this information, and not taking into account any quantity discount offers, what is the calculated EOQ (in units)? (Display your answer to the nearest whole number.) Number Based on this information, sort each quantity discount plan from left to right by dragging the MOST preferred option plan to the left, and the LEAST preferred…arrow_forwardIn less than 150 words, what is an example of what your reflection of core values means to you and your work: Commitment, Perseverance, Community, Service, Pride?arrow_forwardPrepare a report on the following: Part 1: Discuss the role of the corporate secretary in facilitating effective governance in a limited liability company. Include the relationships with directors, shareholders, and other officers. Part 2: Compare and contrast two characteristics of different business entities (sole trader, partnership, and limited liability company). Use examples to recommend the most appropriate type of business entity for the scenario below: Scenario Background Alex, Taylor, and Jordan plan to collaborate to launch a tech startup focused on developing and selling innovative software solutions. Each individual brings unique skills and resources to the venture: Alex: A skilled software developer with technical expertise and a vision for the product. Taylor: A marketing professional with extensive connections in the technology industry, aiming to drive sales and build the brand. Jordan: An investor willing to contribute significant financial resources but…arrow_forward
- Problem 1 (20 Points) Davison Electronics manufactures three LED television monitors, identified as Model A, Model B, and Model C. Davison Electronics four manufacturing plants. Each model has its lowest possible production cost when produced at Plant 1. However, Plant 1 does not have the capacity to handle the total production of all three models. As a result, at least some of the production must be routed to the other manufacturing plants. The following table shows the minimum production requirements for next month, the plant capacities in units per month, and the production cost per unit at each plant: Model Production Cost per Unit Minimum Production Requirements Plant 1 Plant 2 Plant 3 Plant 4 A $25 $28 $37 $34 48,000 B $26 $35 $36 $41 75,000 C $20 $31 $26 $23 60,000 Production Capacity 65,000 50,000 32,000 43,000 Davison’s objective is to determine the cost-minimizing production plan. Without…arrow_forwardSECTION B: TOPIC STRUCTURE CAPSTONE PROJECT TOPIC SUBMISSION TEMPLATE SECTION A: STUDENT DETAILS Student number Title (Mr/Miss/Ms/Mrs) Surname First name/s Title of research Date and year of registration Work Home Contact details Cell Region Date submitted Email 1.1 Title Insert title of the research. Choose a title that captures the essence of your proposed project. 1.2 Background to the Problem This section will be used to create the readers' interest. It can include a specific description of the topic that is to be investigated. A brief preview of the topic and the foundation of the problem should also be given. The researcher can achieve this through building up a detailed background of circumstances that lead to the problem being examined. Therefore, the background helps the reader understand the specific problem addressed by the researcher. This section should not include the background/history of the organisation. The background to the problem should not be more than ½ a page.…arrow_forwardDoes Nike Corporation's emphasis on lean operations help the Vietnamese workforce that still earns $150.00 minimum wage a month since 2014?arrow_forward
- Information Security Innovation within a Contemporary Business Environment All organisations using computers need to consider the security of information they keep. Many organisations utilise Websites for their core business functions and this results in monetary transactions being carried out on the Websites.arrow_forwardPlease help with a complete research report on the topic below: "Information Security Innovation within a Contemporary Business Environment " The format of the report should follow this below.arrow_forward7. Wireless Infrastructure in the Cloud Wireless devices have changed the way organisations and their customers interact. Wireless enabled devices have driven the mindset that wireless networks must be ubiquitous, fast, and constantly available. These are demands that have traditionally put organisations and their user communities in direct conflict with their IT departments, as constructing and maintaining wireless infrastructures are typically time-consuming, complex, and costly endeavours.arrow_forward
- IM.54 A growing online retailer sells thousands of items yet has has one specialty product category with just 30 items. They want to classify these thirty items according to the annual dollar volume (revenue) generated by each item. The table below lists each item number, Annual Sales (in units), and Price per unit: Item # Annual Sales Price 1 221 $25.85 2 446 $14.15 3 8,940 $168.19 4 2,965 $15.99 5 1,322 $29.37 6 2,575 $12.77 7 767 $28.43 8 5,803 $163.01 9 2,673 $20.51 10 642 $14.71 11 4,168 $54.53 12 1,881 $22.55 13 2,417 $29.63 14 5,207 $36.41 15 1,381 $20.55 16 9,635 $173.69 17 17,406 $27.07 18 1,573 $25.99 19 6,471 $64.99 20 6,047 $29.83 21 433 $20.89 22 2,279 $53.59 23 15,532 $106.91 24 1,585 $4.09 25 5,376 $65.23 26 2,965 $37.93 27 2,048 $28.51 28 1,174 $22.99 29 381 $5.57 30 2,930 $3.43 Which item in the table above has the highest annual dollar volume? In the answer field below, write the ITEM # that…arrow_forwardIM.84 An outdoor equipment manufacturer sells a rugged water bottle to complement its product line. They sell this item to a variety of sporting goods stores and other retailers. The manufacturer offers quantity discounts per the following discount schedule: Option Plan Quantity Price A 1 - 2,199 $5.00 B 2,200 - 3,699 $4.55 C 3,700+ $3.90 A large big-box retailer expects to sell 9,200 units this year. This retailer estimates that it incurs an internal administrative cost of $235 each time it places an order with the manufacturer. Holding cost for the retailer is $60 per case per year. (There are 52 units or water bottles per case.)Based on this information, and not taking into account any quantity discount offers, what is the calculated EOQ (in units)? (Display your answer to the nearest whole number.) Based on this information, sort each quantity discount plan from left to right by dragging the MOST preferred option plan to the left, and the LEAST preferred option…arrow_forwardPlease provide detailed solutions to the following problems/exercises (4 problems/exercises x 9 points each): 1) View the video ON Unveils ‘Lightspray’ Technology (4.55 mins, Ctrl+Click in the link), and The Secret of Lightspray (8.27 mins, Ctrl+Click in the link), answer the following questions: https://www.youtube.com/watch?v=wjmeaC-wlZs a) What is new about the design of ON’s shoes? b) How will ON’s new manufacturing technique affect location planning for footwear firms? c) How does ON focus on it sustainability strategy? Note: As a rough guideline, please try to keep the written submission to one or two paragraphs for each of the questions. 2) Unimed Hospital currently processes patient admissions through three admitting clerks who are set up to work in series, with respective reliabilities of 0.96, 0.95, and 0.90 (see figure below). a) Find the reliability of the current admission process. Due to rising patient complaints, the hospital administrator, Chimeg…arrow_forward
 Practical Management ScienceOperations ManagementISBN:9781337406659Author:WINSTON, Wayne L.Publisher:Cengage,
Practical Management ScienceOperations ManagementISBN:9781337406659Author:WINSTON, Wayne L.Publisher:Cengage,

