
(a)
The velocity of the particle.
(a)
Explanation of Solution
Given:
The position of the particle at
The position of the particle at
The velocity of the particle is
Formula used:
Write the expression for the average velocity.
Here,
Here,
Write the expression for the average velocity of the particle.
Here,
Solve the above equation for
Calculation:
Substitute
Substitute
Conclusion:
Thus, the initial velocity is
(b)
The acceleration of the particle.
(b)
Explanation of Solution
Given:
The position of the particle at
The position of the particle at 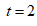 is
is
The velocity of the particle is
Formula used:
Write the expression for the acceleration of the particle.
Here,
is the change in the velocity vector and 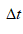 is the change in time.
is the change in time.
Here,
Calculation:
Substitute
Conclusion:
The acceleration of the particle is
(c)
The velocity of the particle as the function of time.
(c)
Explanation of Solution
Given:
The position of the particle at 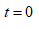 is
is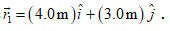 .
.
The position of the particle at 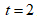 is
is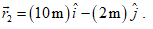
The velocity of the particle is
Formula used:
Write the expression for the velocity of the particle as the function of time.
Here,
Calculation:
Substitute
Conclusion:
Thus, the velocity of the particle as the function of timeis
(d)
The position vector of the particle as the function of time.
(d)
Explanation of Solution
Given:
The position of the particle at 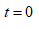 is
is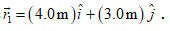 .
.
The position of the particle at 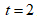 is
is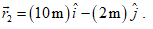
The velocity of the particle is
Formula used:
Write the expression for the position vector as the function of time.
Calculation:
Substitute
Conclusion:
The position vector of the particle as the function of time is:
Want to see more full solutions like this?
Chapter 3 Solutions
Physics for Scientists and Engineers
 Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill
Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University
University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning





