
Concept explainers
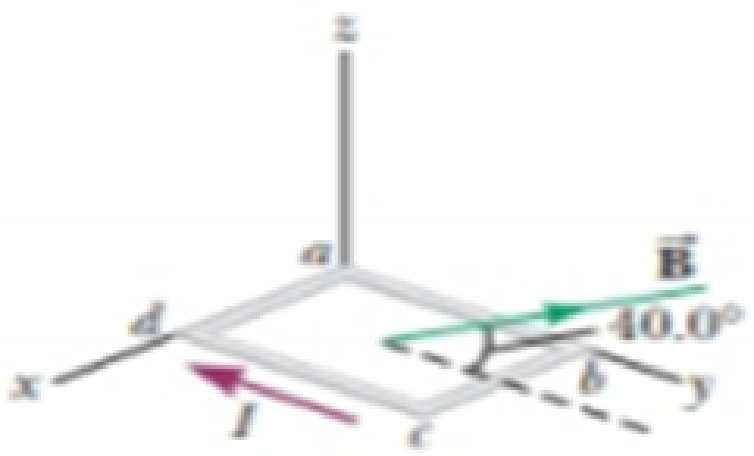
A rectangular loop of wire has dimensions 0.500 m by 0.300 m. The loop is pivoted at the x axis and lies in the xy plane as shown in Figure P28.34. A uniform magnetic field of magnitude 1.50 T is directed at an angle of 40.0° with respect to the y axis with field lines parallel to the yz plane. The loop carries a current of 0.900 A in the direction shown. (Ignore gravitation.) We wish to evaluate the torque on the current loop. (a) What is the direction of the magnetic force exerted on wire segment ab? (b) What is the direction of the torque associated with this force about an axis through the origin? (c) What is the direction of the magnetic force exerted on segment cd? (d) What is the direction of the torque associated with this force about an axis through the origin? (e) Can the forces examined in parts (a) and (c) combine to cause the Loop to rotate around the x axis? (f) Can they affect the motion of the loop in any way? Explain. (g) What is the direction of the magnetic force exerted on segment bc? (h) What is the direction of the torque associated with this force about an axis through the origin? (i) What is the torque on segment ad about an axis through the origin? (j) From the point of view of Figure P28.34, once the loop is released from rest at the position shown, will it rotate clockwise or counterclockwise around the x axis? (k) Compute the magnitude of the magnetic moment of the loop. (l) What is the angle between the magnetic moment sector and the magnetic field? (m) Compute the torque on the loop using the results to parts (k) and (l).
Figure P28.34
(a)
The direction of the magnetic force exerted on wire segment
Answer to Problem 34P
The direction of the force is in the positive x-axis.
Explanation of Solution
Given Info: The length of the rectangular loop is
According to the Fleming left hand rule, if a thumb, an index finger and a middle finger of a right hand is stretch in a position that they formed mutually perpendicular to each other, there the direction of thumb will indicate the direction of force, the direction of index finger will indicate the direction of magnetic field and the direction of middle finger will indicate the direction of current.
By using the Fleming left hand rule, if the middle finger shows the direction of current in segment
Conclusion:
Therefore, the direction of the force is in the positive x-axis.
(b)
The direction of the torque associated with the above force about an axis through the origin.
Answer to Problem 34P
The direction of the torque associated with the force on segment
Explanation of Solution
Given Info: The length of the rectangular loop is
The Formula to calculate the torque associated with the force is,
Here,
Substitute
The torque associated in the above expression in the negative of the unit vector
Conclusion:
Therefore, the direction of the torque associated with the force on segment
(c)
The direction of the magnetic force exerted on the segment
Answer to Problem 34P
The direction of the magnetic force exerted on the segment
Explanation of Solution
Given Info: The length of the rectangular loop is
The Formula to calculate the magnetic force on the wire segment
Here,
Substitute
In the above expression it is shown that the magnetic force is in the negative of the unit vector
Conclusion:
Therefore, the direction of the magnetic force exerted on the segment
(d)
The direction of the torque associated with the force on the segment
Answer to Problem 34P
The direction of the torque associated with the force on segment
Explanation of Solution
Given Info: The length of the rectangular loop is
The Formula to calculate the torque associated with the force is,
Here,
Substitute
The torque associated in the above expression is in the negative of the unit vector
Conclusion:
Therefore, the direction of the torque associated with the force on segment
(e)
Whether the force examined in part (a) and (c) combine to cause the loop to rotate around the x-axis.
Answer to Problem 34P
The magnetic force cannot rotate the loop.
Explanation of Solution
Given Info: The length of the rectangular loop is
As the force examined on the segment
Thus the net force on the rectangular loop become zero.
Conclusion:
Therefore, the magnetic force cannot rotate the loop.
(f)
Whether the above forces affect the motion of the loop.
Answer to Problem 34P
The magnetic force will only rotate the loop and will not affect the motion of the loop.
Explanation of Solution
Given Info: The length of the rectangular loop is
According to the expression in the equation (2) if the magnetic field, current and the length of the loop is constant then its magnetic force will be constant too. In the given problem the magnetic field, the current and the length of the loop is constant, therefore, the magnetic force is constant. Hence this magnetic force will only rotate the loop and will not affect the motion of the loop.
Conclusion:
Therefore, the magnetic force will only rotate the loop and will not affect the motion of the loop.
(g)
The direction of the magnetic force exerted on segment
Answer to Problem 34P
The magnetic force on segment
Explanation of Solution
Given Info: The length of the rectangular loop is
The Formula to calculate the magnetic force on the wire segment
Here,
Substitute
In the above expression it is shown that the magnetic force is in the negative of the unit vector
Conclusion:
Therefore, the magnetic force on segment
(h)
The direction of the torque associated with the force on the segment
Answer to Problem 34P
The direction of the torque associated with the force on segment
Explanation of Solution
Given Info: The length of the rectangular loop is
The Formula to calculate the torque associated with the force is,
Here,
Substitute
The torque associated in the above expression is in the positive of the unit vector
Conclusion:
Therefore, the direction of the torque associated with the force on segment
(i)
The direction of the torque on the segment
Answer to Problem 34P
The torque on the segment
Explanation of Solution
Given Info: The length of the rectangular loop is
The Formula to calculate the torque associated with the force is,
The segment
Conclusion:
Therefore, the torque on the segment
(j)
Whether the loop locate itself clockwise or anticlockwise.
Answer to Problem 34P
The rectangular loop will rotate in the anticlockwise direction.
Explanation of Solution
Given Info: The length of the rectangular loop is
As the torque on the segment
Conclusion:
Therefore, the rectangular loop will rotate in the anticlockwise direction.
(k)
The magnitude of the magnetic moment of the loop.
Answer to Problem 34P
The magnitude of the magnetic moment of the loop is
Explanation of Solution
Given Info: The length of the rectangular loop is
The formula to calculate the magnetic moment of the loop is,
Here,
Substitute
Conclusion:
Therefore, the magnitude of the magnetic moment of the loop is
(l)
The angle between the magnetic moment vector and magnetic field.
Answer to Problem 34P
The angle between the magnetic moment and magnetic field is
Explanation of Solution
Given Info: The length of the rectangular loop is
It is given that the current if lowing in clockwise direction therefore, here follow the principle of right hand thumb rule, if the finger is curl in the direction of current then the thumb will indicate the moment of magnetic field. Thus, the direction of magnetic moment is downward. That is along the negative z direction. The angle between the magnetic moment and magnetic field is,
Conclusion:
Therefore, the angle between the magnetic moment and magnetic field is
(m)
The torque on the loop using the results of part (k) and (l).
Answer to Problem 34P
The torque on the loop is
Explanation of Solution
Given Info: The length of the rectangular loop is
Formula to calculate the torque in current carrying wire is,
Substitute
Conclusion:
Therefore, the torque on the loop is
Want to see more full solutions like this?
Chapter 28 Solutions
Physics for Scientists and Engineers with Modern Physics
Additional Science Textbook Solutions
College Physics: A Strategic Approach (3rd Edition)
Fundamentals Of Thermodynamics
MARINE BIOLOGY
Genetics: From Genes to Genomes
Chemistry: An Introduction to General, Organic, and Biological Chemistry (13th Edition)
- help me with the experimental set up for the excel i did. the grapharrow_forwardWhich of the following best describes how to calculate the average acceleration of any object? Average acceleration is always halfway between the initial acceleration of an object and its final acceleration. Average acceleration is always equal to the change in velocity of an object divided by the time interval. Average acceleration is always equal to the displacement of an object divided by the time interval. Average acceleration is always equal to the change in speed of an object divided by the time interval.arrow_forwardThe figure shows the velocity versus time graph for a car driving on a straight road. Which of the following best describes the acceleration of the car? v (m/s) t(s) The acceleration of the car is negative and decreasing. The acceleration of the car is constant. The acceleration of the car is positive and increasing. The acceleration of the car is positive and decreasing. The acceleration of the car is negative and increasing.arrow_forward
- Which figure could represent the velocity versus time graph of a motorcycle whose speed is increasing? v (m/s) v (m/s) t(s) t(s)arrow_forwardUnlike speed, velocity is a the statement? Poisition. Direction. Vector. Scalar. quantity. Which one of the following completesarrow_forwardNo chatgpt pls will upvote Already got wrong chatgpt answerarrow_forward
- 3.63 • Leaping the River II. A physics professor did daredevil stunts in his spare time. His last stunt was an attempt to jump across a river on a motorcycle (Fig. P3.63). The takeoff ramp was inclined at 53.0°, the river was 40.0 m wide, and the far bank was 15.0 m lower than the top of the ramp. The river itself was 100 m below the ramp. Ignore air resistance. (a) What should his speed have been at the top of the ramp to have just made it to the edge of the far bank? (b) If his speed was only half the value found in part (a), where did he land? Figure P3.63 53.0° 100 m 40.0 m→ 15.0 marrow_forwardPlease solve and answer the question correctly please. Thank you!!arrow_forwardYou throw a small rock straight up from the edge of a highway bridge that crosses a river. The rock passes you on its way down, 5.00 s after it was thrown. What is the speed of the rock just before it reaches the water 25.0 m below the point where the rock left your hand? Ignore air resistance.arrow_forward
- Help me make a visualize experimental setup using a word document. For the theory below.arrow_forwardHow to solve this, given answerarrow_forwardThree point-like charges are placed at the corners of a square as shown in the figure, 28.0 cm on each side. Find the minimum amount of work required by an external force to move the charge q1 to infinity. Let q1=-2.10 μC, q2=+2.40 μС, q3=+3.60 μC.arrow_forward
 Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning





