Calculus Volume 3
16th Edition
ISBN: 9781938168079
Author: Gilbert Strang, Edwin Jed Herman
Publisher: OpenStax
expand_more
expand_more
format_list_bulleted
Concept explainers
Textbook Question
Chapter 2.7, Problem 363E
Use the following ?gure as an aid in identifying the relationship between the rectangular, cylindrical, and spherical
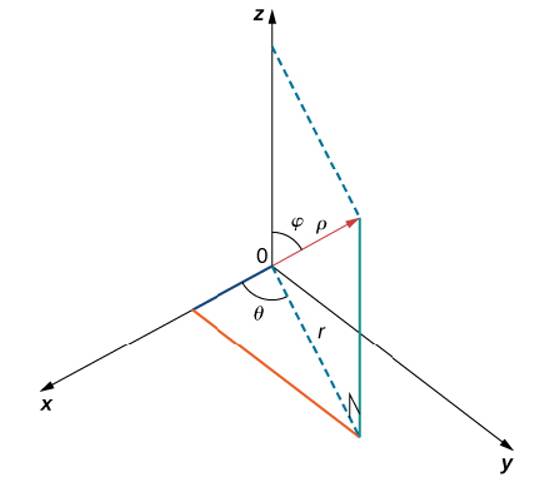
For the following exercises, the cylindrical coordinates
363.
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Answer questions 8.1.13 and 8.2.10 respectively
To help consumers in purchasing a laptop computer, Consumer Reports calculates an overall test score for each computer tested based upon rating factors such as ergonomics, portability, performance, display, and battery life. Higher overall scores indicate better test results. The following data show the average retail price and the overall score for ten 13-inch models (Consumer Reports website, October 25, 2012).
Brand & Model
Price ($)
Overall Score
Samsung Ultrabook NP900X3C-A01US
1250
83
Apple MacBook Air MC965LL/A
1300
83
Apple MacBook Air MD231LL/A
1200
82
HP ENVY 13-2050nr Spectre XT
950
79
Sony VAIO SVS13112FXB
800
77
Acer Aspire S5-391-9880 Ultrabook
1200
74
Apple MacBook Pro MD101LL/A
1200
74
Apple MacBook Pro MD313LL/A
1000
73
Dell Inspiron I13Z-6591SLV
700
67
Samsung NP535U3C-A01US
600
63
a. Select a scatter diagram with price as the independent variable.
b. What does the scatter diagram developed in part (a) indicate about the relationship…
Answer questions 8.2.6, 8.2.7 and 8.2.9 respectively
Chapter 2 Solutions
Calculus Volume 3
Ch. 2.1 - For the following exercises, consider points...Ch. 2.1 - For the following exercises, consider points...Ch. 2.1 - For the following exercises, consider points...Ch. 2.1 - For the following exercises, consider points...Ch. 2.1 - For the following exercises, consider points...Ch. 2.1 - For the following exercises, consider points...Ch. 2.1 - For the following exercises, consider points...Ch. 2.1 - For the following exercises, consider points...Ch. 2.1 - For the following exercises, consider points...Ch. 2.1 - For the following exercises, consider points...
Ch. 2.1 - For the following exercises, consider points...Ch. 2.1 - For the following exercises, consider points...Ch. 2.1 - For the following exercises, consider points...Ch. 2.1 - For the following exercises, consider points...Ch. 2.1 - Far the following exercises, use the given...Ch. 2.1 - Far the following exercises, use the given...Ch. 2.1 - Far the following exercises, use the given...Ch. 2.1 - Far the following exercises, use the given...Ch. 2.1 - Far the following exercises, use the given...Ch. 2.1 - Far the following exercises, use the given...Ch. 2.1 - Far the following exercises, use the given...Ch. 2.1 - Far the following exercises, use the given...Ch. 2.1 - Far the following exercises, use the given...Ch. 2.1 - Far the following exercises, use the given...Ch. 2.1 - For the following exercises, find vector v with...Ch. 2.1 - For the following exercises, find vector v with...Ch. 2.1 - For the following exercises, find vector v with...Ch. 2.1 - For the following exercises, find vector v with...Ch. 2.1 - For the following exercises, find the component...Ch. 2.1 - For the following exercises, find the component...Ch. 2.1 - For the following exercises, find the component...Ch. 2.1 - For the following exercises, find the component...Ch. 2.1 - For the following exercises, find the component...Ch. 2.1 - For the following exercises, find the component...Ch. 2.1 - For the following exercises, vector u is given....Ch. 2.1 - For the following exercises, vector u is given....Ch. 2.1 - Let a=a1,a2,b=b1,b2 , and c=c1,c2 be three nonzero...Ch. 2.1 - Consider vectors a=2,4,b=1,2, and c=0 . Determine...Ch. 2.1 - Let P(x0,f(x0)) be a fixed point on the graph of...Ch. 2.1 - Consider the function f(x)=x4 , where x. Determine...Ch. 2.1 - Consider f and g two functions defined on the same...Ch. 2.1 - Find x such that vectors a=x,sinx and b=x,cosx are...Ch. 2.1 - Calculate the coordinates of point D such that...Ch. 2.1 - Consider the points A(2,1),B(10,6),C(13,4) , and...Ch. 2.1 - The speed of an object is the magnitude of its...Ch. 2.1 - A baseball player throws a baseball at an angle of...Ch. 2.1 - A bullet is fired with an initial velocity of...Ch. 2.1 - [T] A 65kg sprinter exerts a force of 798N at a 19...Ch. 2.1 - [T] Two forces, a horizontal force of 45lb and...Ch. 2.1 - [T] Two fumes, a vertical fence of 26lb and...Ch. 2.1 - [T] Three forces act an object. Two of the fences...Ch. 2.1 - Three forces with magnitudes 80lb,120lb, and 60lb...Ch. 2.1 - [T] An airplane is flying in the direction of 43...Ch. 2.1 - [T] A boat is traveling in the water at 30mph in a...Ch. 2.1 - [T] A 50-lb weight is hung by a cable so that the...Ch. 2.1 - [T] A 62-lh weight hangs from a nope that makes...Ch. 2.1 - [T] A 1500lb boat is parked on a ramp that makes...Ch. 2.1 - [T] An 85lb box is at rest on a 26 incline....Ch. 2.1 - A guy-wire supports a pole that is 75ft high. One...Ch. 2.1 - A telephone pole guy-wire has an angle of...Ch. 2.2 - Consider a rectangular box with one of the...Ch. 2.2 - Find the coordinates of point P and determine its...Ch. 2.2 - For the following exercises, describe and graph...Ch. 2.2 - For the following exercises, describe and graph...Ch. 2.2 - For the following exercises, describe and graph...Ch. 2.2 - For the following exercises, describe and graph...Ch. 2.2 - Write the equation of the plane passing through...Ch. 2.2 - Write the equation of the plane passing through...Ch. 2.2 - Find an equation of the plane passing through...Ch. 2.2 - Find an equation of the plane passing through...Ch. 2.2 - For the following exercises, find the equation of...Ch. 2.2 - For the following exercises, find the equation of...Ch. 2.2 - For the following exercises, find the equation of...Ch. 2.2 - For the following exercises, find the equation of...Ch. 2.2 - For the following exercises, find the center and...Ch. 2.2 - For the following exercises, find the center and...Ch. 2.2 - For the following exercises, express vector PQ...Ch. 2.2 - For the following exercises, express vector PQ...Ch. 2.2 - For the following exercises, express vector PQ...Ch. 2.2 - For the following exercises, express vector PQ...Ch. 2.2 - For the following exercises, express vector PQ...Ch. 2.2 - For the following exercises, express vector PQ...Ch. 2.2 - For the following exercises, use the given vectors...Ch. 2.2 - For the following exercises, use the given vectors...Ch. 2.2 - For the following exercises, use the given vectors...Ch. 2.2 - For the following exercises, use the given vectors...Ch. 2.2 - For the following exercises, vectors u and v are...Ch. 2.2 - For the following exercises, vectors u and v are...Ch. 2.2 - For the following exercises, vectors u and v are...Ch. 2.2 - For the following exercises, vectors u and v are...Ch. 2.2 - For the following exercises, find the unit vector...Ch. 2.2 - For the following exercises, find the unit vector...Ch. 2.2 - For the following exercises, find the unit vector...Ch. 2.2 - For the following exercises, find the unit vector...Ch. 2.2 - For the following exercises, find the unit vector...Ch. 2.2 - For the following exercises, find the unit vector...Ch. 2.2 - Determine whether AB and PQ are equivalent...Ch. 2.2 - Determine whether the vectors AB and PQ are...Ch. 2.2 - For the following exercises, find vector u with a...Ch. 2.2 - For the following exercises, find vector u with a...Ch. 2.2 - For the following exercises, find vector u with a...Ch. 2.2 - For the following exercises, find vector u with a...Ch. 2.2 - Determine a vector of magnitude 5 in the direction...Ch. 2.2 - Find a vector of magnitude 2 that points in the...Ch. 2.2 - Consider the points A(2,,0),B(0,1,), and C(1,1,),...Ch. 2.2 - Consider points A(,0,0),B(0,,0), and C(,,), where ...Ch. 2.2 - Let P(x,y,z) be a point situated at an equal...Ch. 2.2 - Let P(x,y,z) be a point situated at an equal...Ch. 2.2 - The points A,B, and C are collinear (in this...Ch. 2.2 - Show that points A(1,0,1),B(0,1,1) and C(1,1,1)...Ch. 2.2 - [T] A force F of 50N acts on a particle in the...Ch. 2.2 - [T] A force F of 40N acts on a box in the...Ch. 2.2 - If F is a force that moves an object from point...Ch. 2.2 - A box is pulled 4 yd horizontally in the x...Ch. 2.2 - The sum of the forces acting on an object is...Ch. 2.2 - [T] Let Fk=1,k,k2,k=1,...,n be n forces acting on...Ch. 2.2 - The force of gravity F acting on an object is...Ch. 2.2 - A 5-kg pendant chandelier is designed such that...Ch. 2.2 - [T] A 30-kg block of cement is suspended by three...Ch. 2.2 - Two soccer players are practicing for an upcoming...Ch. 2.2 - Let r(t)=x(t),y(t),z(t) be the position vector of...Ch. 2.2 - [T] Let r(t)=t,2t2,4t2 be the position vector of a...Ch. 2.3 - For the following exercises, the vectors u and v...Ch. 2.3 - For the following exercises, the vectors u and v...Ch. 2.3 - For the following exercises, the vectors u and v...Ch. 2.3 - For the following exercises, the vectors u and v...Ch. 2.3 - For the following exercises, the vectors a,b, and...Ch. 2.3 - For the following exercises, the vectors a,b, and...Ch. 2.3 - For the following exercises, the vectors a,b, and...Ch. 2.3 - For the following exercises, the vectors a,b, and...Ch. 2.3 - For the following exercises, the two-dimensional...Ch. 2.3 - For the following exercises, the two-dimensional...Ch. 2.3 - For the following exercises, the two-dimensional...Ch. 2.3 - For the following exercises, the two-dimensional...Ch. 2.3 - For the following exercises, find the measure 0f...Ch. 2.3 - For the following exercises, find the measure 0f...Ch. 2.3 - For the following exercises, find the measure 0f...Ch. 2.3 - For the following exercises, find the measure 0f...Ch. 2.3 - For the following exercises, find the measure 0f...Ch. 2.3 - For the following exercises, find the measure 0f...Ch. 2.3 - For the following exercises determine whether the...Ch. 2.3 - For the following exercises determine whether the...Ch. 2.3 - For the following exercises determine whether the...Ch. 2.3 - For the following exercises determine whether the...Ch. 2.3 - For the following exercises determine whether the...Ch. 2.3 - For the following exercises determine whether the...Ch. 2.3 - For the following exercises determine whether the...Ch. 2.3 - For the following exercises determine whether the...Ch. 2.3 - For the following exercises determine whether the...Ch. 2.3 - For the following exercises determine whether the...Ch. 2.3 - [T] Consider the points P(4,5) and Q(5,7) ....Ch. 2.3 - [T] Consider points A(1,1),B(2,7) , and C(6,3)....Ch. 2.3 - Determine the measure of angle A in triangle ABC ,...Ch. 2.3 - Consider points P(3,7,2) and Q(1,1,3). Determine...Ch. 2.3 - For the following exercises, determine which (if...Ch. 2.3 - For the following exercises, determine which (if...Ch. 2.3 - For the following exercises, determine which (if...Ch. 2.3 - For the following exercises, determine which (if...Ch. 2.3 - For the following exercises, determine which (if...Ch. 2.3 - For the following exercises, determine which (if...Ch. 2.3 - For the following problems, the vector u is given....Ch. 2.3 - For the following problems, the vector u is given....Ch. 2.3 - For the following problems, the vector u is given....Ch. 2.3 - For the following problems, the vector u is given....Ch. 2.3 - For the following problems, the vector u is given....Ch. 2.3 - For the following problems, the vector u is given....Ch. 2.3 - For the following exercises, the vectors u and v...Ch. 2.3 - For the following exercises, the vectors u and v...Ch. 2.3 - For the following exercises, the vectors u and v...Ch. 2.3 - For the following exercises, the vectors u and v...Ch. 2.3 - For the following exercises, the vectors u and v...Ch. 2.3 - For the following exercises, the vectors u and v...Ch. 2.3 - A methane molecule has a carbon atom situated at...Ch. 2.3 - [T] Find the vectors that join the center of a...Ch. 2.3 - Find the work done by force F=5,6,2 (measured in...Ch. 2.3 - [T] A sled is pulled by exerting a force of 100N...Ch. 2.3 - [T] A father is pulling his son on a sled at an...Ch. 2.3 - [T] A car is towed using a force of 1600N . The...Ch. 2.3 - [T] A boat sails north aided by a wind blowing in...Ch. 2.3 - Vector p=150,225,375 represents the price of...Ch. 2.3 - [T] Two forces F1 and F2 are represented by...Ch. 2.3 - [T] Consider r(t)=cost,sint,2t the position vector...Ch. 2.4 - For the following exercises, the vectors u and v...Ch. 2.4 - For the following exercises, the vectors u and v...Ch. 2.4 - For the following exercises, the vectors u and v...Ch. 2.4 - For the following exercises, the vectors u and v...Ch. 2.4 - `For the following exercises, the vectors u and v...Ch. 2.4 - For the following exercises, the vectors u and v...Ch. 2.4 - In the following exercises, vectors u and v are...Ch. 2.4 - In the following exercises, vectors u and v are...Ch. 2.4 - In the following exercises, vectors u and v are...Ch. 2.4 - In the following exercises, vectors u and v are...Ch. 2.4 - In the following exercises, vectors u and v are...Ch. 2.4 - In the following exercises, vectors u and v are...Ch. 2.4 - In the following exercises, vectors u and v are...Ch. 2.4 - In the following exercises, vectors u and v are...Ch. 2.4 - Calculate the determinant |ijk117203| .Ch. 2.4 - Calculate the determinant |ijk034161| .Ch. 2.4 - For the following exercises, the vector u and v...Ch. 2.4 - For the following exercises, the vector u and v...Ch. 2.4 - Find vector (a2b)c , where...Ch. 2.4 - Find vector c(a+3b) , where...Ch. 2.4 - [T] Use the cross product uv to find the acute...Ch. 2.4 - [T] Use the cross product uv to find the obtuse...Ch. 2.4 - Use the sine and cosine of the angle between two...Ch. 2.4 - Verify Lagrange’s identity uv2=u2v2(uv)2 for...Ch. 2.4 - Nonzero vectors u and v are called collinear if...Ch. 2.4 - Nonzero vectors u and v are called collinear if...Ch. 2.4 - Find the area of the parallelogram with adjacent...Ch. 2.4 - Find the area of the parallelogram with adjacent...Ch. 2.4 - Consider paints A(3,1,2),B(2,1,5), and C(1,2,2)....Ch. 2.4 - Consider points A(2,3,4),B(0,1,2), and C(1,2,0)....Ch. 2.4 - In the following exercises, vectors u,v, and w are...Ch. 2.4 - In the following exercises, vectors u,v, and w are...Ch. 2.4 - In the following exercises, vectors u,v, and w are...Ch. 2.4 - In the following exercises, vectors u,v, and w are...Ch. 2.4 - Find vectors a,b, and c with a triple scalar...Ch. 2.4 - The triple scalar product of vector a,b, and c is...Ch. 2.4 - Consider the parallelepiped with edges OA,OB, and...Ch. 2.4 - Consider points A(,0,0),B(0,,0), and C(0,0,), with...Ch. 2.4 - Let u,v, and w be three-dimensional vectors and c...Ch. 2.4 - Show that vectors u=1,0,8,v=0,1,6, and w=1,9,3...Ch. 2.4 - Nonzero vectors u,v, and w are said to be linearly...Ch. 2.4 - Consider vectors u=1,4,7,v=2,1,4,w=0,9,18, and...Ch. 2.4 - Consider points A(0,0,2),B(1,0,2),C(1,1,2), and...Ch. 2.4 - Show that vectors i+j,ij, and i+j+k are linearly...Ch. 2.4 - Let u=u1,u2,0 and v=v1,v2,0, be two-dimensional...Ch. 2.4 - Consider points P(2,1),Q(4,2) and R(1,2). Find the...Ch. 2.4 - Determine a vector of magnitude 10 perpendicular...Ch. 2.4 - Determine a unit vector perpendicular to the plane...Ch. 2.4 - Consider u and v two three-dimensional vectors. If...Ch. 2.4 - [T] Assume that the magnitudes of two nonzero...Ch. 2.4 - Find all vectors w=w1,w2,w3 that satisfy the...Ch. 2.4 - - Solve the w1,0,1=3,0,3, where w=w1,w2,w3 is a...Ch. 2.4 - [T] A mechanic uses a 12in . wrench to turn a...Ch. 2.4 - [T] A boy applies the brakes on a bicycle by...Ch. 2.4 - [T] Find the magnitude of the force that needs to...Ch. 2.4 - [T] What is the magnitude of the force required to...Ch. 2.4 - [T] The fence vector F acting on a proton with all...Ch. 2.4 - [T] The fence vector F acting on a proton with an...Ch. 2.4 - [T] Consider r(t)=cost,sint,2t the position vector...Ch. 2.4 - A solar panel is mounted 011 the roof of a house....Ch. 2.5 - Figure 2.73 Industrial pipe installations often...Ch. 2.5 - Figure 2.73 Industrial pipe installations often...Ch. 2.5 - Figure 2.73 Industrial pipe installations often...Ch. 2.5 - Figure 2.73 Industrial pipe installations often...Ch. 2.5 - Figure 2.73 Industrial pipe installations often...Ch. 2.5 - Figure 2.73 Industrial pipe installations often...Ch. 2.5 - Figure 2.73 Industrial pipe installations often...Ch. 2.5 - Figure 2.73 Industrial pipe installations often...Ch. 2.5 - Figure 2.73 Industrial pipe installations often...Ch. 2.5 - In the following exercises, points P and Q are...Ch. 2.5 - In the following exercises, points P and Q are...Ch. 2.5 - In the following exercises, points P and Q are...Ch. 2.5 - In the following exercises, points P and Q are...Ch. 2.5 - For the following exercises, point P and vector v...Ch. 2.5 - For the following exercises, point P and vector v...Ch. 2.5 - For the following exercises, point P and vector v...Ch. 2.5 - For the following exercises, point P and vector v...Ch. 2.5 - For the following exercises, line L is given. Find...Ch. 2.5 - For the following exercises, line L is given. Find...Ch. 2.5 - For the following exercises, line L is given. Find...Ch. 2.5 - For the following exercises, line L is given. Find...Ch. 2.5 - For the following exercises, lines L1 and L2 are...Ch. 2.5 - For the following exercises, lines L1 and L2 are...Ch. 2.5 - For the following exercises, lines L1 and L2 are...Ch. 2.5 - For the following exercises, lines L1 and L2 are...Ch. 2.5 - For the following exercises, lines L1 and L2 are...Ch. 2.5 - For the following exercises, lines L1 and L2 are...Ch. 2.5 - For the following exercises, Lines L1 and L2 are...Ch. 2.5 - For the following exercises, Lines L1 and L2 are...Ch. 2.5 - For the following exercises, Lines L1 and L2 are...Ch. 2.5 - For the following exercises, Lines L1 and L2 are...Ch. 2.5 - For the following exercises, Lines L1 and L2 are...Ch. 2.5 - For the following exercises, Lines L1 and L2 are...Ch. 2.5 - For the following exercises, point P and vector n...Ch. 2.5 - For the following exercises, point P and vector n...Ch. 2.5 - For the following exercises, point P and vector n...Ch. 2.5 - For the following exercises, point P and vector n...Ch. 2.5 - For the following exercises, the equation of a...Ch. 2.5 - For the following exercises, the equation of a...Ch. 2.5 - For the following exercises, the equation of a...Ch. 2.5 - For the following exercises, the equation of a...Ch. 2.5 - Given paint P(1,2,3) and vector n=i+j , find point...Ch. 2.5 - Show there is no plane perpendicular to n=i+j that...Ch. 2.5 - Find parametric equations 0f the Line passing...Ch. 2.5 - Find symmetric equations of the line passing...Ch. 2.5 - Show that line x12=y+13=z24 is parallel to plane...Ch. 2.5 - Find the real number such that the line of...Ch. 2.5 - For the following exercises, points P,Q, and R are...Ch. 2.5 - For the following exercises, points P,Q, and R are...Ch. 2.5 - Consider the planes of equations x+y+z=1 and x+z=0...Ch. 2.5 - Consider the planes of equations y+z2=0 and xy=0 ....Ch. 2.5 - Find the scalar equation of the plane that passes...Ch. 2.5 - Find the general equation of the plane that passes...Ch. 2.5 - Determine whether the Line of parametric equations...Ch. 2.5 - Determine whether the Line of parametric equations...Ch. 2.5 - Find the distance from point P(1,5,4) to the plane...Ch. 2.5 - Find the distance from point P(1,2,3) to the plane...Ch. 2.5 - For the following exercises, the equations of two...Ch. 2.5 - For the following exercises, the equations of two...Ch. 2.5 - For the following exercises, the equations of two...Ch. 2.5 - For the following exercises, the equations of two...Ch. 2.5 - Show that the lines of equations x=t,y=1+t,z=2+t,t...Ch. 2.5 - Show that the lines of equations...Ch. 2.5 - Consider point C(3,2,4) and the plane of equation...Ch. 2.5 - Consider the plane of equation xyz8=0. Find the...Ch. 2.5 - Two children are playing with a ball. The girl...Ch. 2.5 - [T] John allocates d dollars to consume monthly...Ch. 2.5 - [T] Consider r(t)=sint,cost,2t the position vector...Ch. 2.5 - [T] A solar panel is mounted on the roof of a...Ch. 2.6 - For the following exercises, sketch and describe...Ch. 2.6 - For the following exercises, sketch and describe...Ch. 2.6 - For the following exercises, sketch and describe...Ch. 2.6 - For the following exercises, sketch and describe...Ch. 2.6 - For the following exercises, sketch and describe...Ch. 2.6 - For the following exercises, sketch and describe...Ch. 2.6 - For the following exercises, the graph of a...Ch. 2.6 - For the following exercises, the graph of a...Ch. 2.6 - For the following exercises, the graph of a...Ch. 2.6 - For the following exercises, the graph of a...Ch. 2.6 - For the fallowing exercises, match the given...Ch. 2.6 - For the fallowing exercises, match the given...Ch. 2.6 - For the fallowing exercises, match the given...Ch. 2.6 - For the fallowing exercises, match the given...Ch. 2.6 - For the fallowing exercises, match the given...Ch. 2.6 - For the fallowing exercises, match the given...Ch. 2.6 - For the following exercises, rewrite the given...Ch. 2.6 - For the following exercises, rewrite the given...Ch. 2.6 - For the following exercises, rewrite the given...Ch. 2.6 - For the following exercises, rewrite the given...Ch. 2.6 - For the following exercises, rewrite the given...Ch. 2.6 - For the following exercises, rewrite the given...Ch. 2.6 - For the following exercises, rewrite the given...Ch. 2.6 - For the following exercises, rewrite the given...Ch. 2.6 - For the following exercises, rewrite the given...Ch. 2.6 - For the following exercises, rewrite the given...Ch. 2.6 - For the following exercises, rewrite the given...Ch. 2.6 - For the following exercises, rewrite the given...Ch. 2.6 - For the following exercises, find the trace of the...Ch. 2.6 - For the following exercises, find the trace of the...Ch. 2.6 - For the following exercises, find the trace of the...Ch. 2.6 - For the following exercises, find the trace of the...Ch. 2.6 - For the following exercises, find the trace of the...Ch. 2.6 - For the following exercises, find the trace of the...Ch. 2.6 - Use the graph of the given quadric surface to...Ch. 2.6 - Use the graph of the given quadric surface to...Ch. 2.6 - For the following exercises, the equation of a...Ch. 2.6 - For the following exercises, the equation of a...Ch. 2.6 - For the following exercises, the equation of a...Ch. 2.6 - For the following exercises, the equation of a...Ch. 2.6 - For the following exercises, the equation of a...Ch. 2.6 - For the following exercises, the equation of a...Ch. 2.6 - Write the standard form of the equation of the...Ch. 2.6 - Write the standard form of the equation of the...Ch. 2.6 - Determine the intersection points of elliptic cone...Ch. 2.6 - Determine the intersection points of parabolic...Ch. 2.6 - Find the equation of the quadric surface with...Ch. 2.6 - Find the equation of the quadric surface with...Ch. 2.6 - If the surface of a parabolic reflector is...Ch. 2.6 - Consider the parabolic reflector described by...Ch. 2.6 - Show that quadric surface...Ch. 2.6 - Show that quadric surface x2+y2+z22xy+2yz1=0...Ch. 2.6 - [T] The intersection between cylinder (x1)2+y2=1...Ch. 2.6 - Hyperboloid of one sheet 25x2+25y2z2=25 and...Ch. 2.6 - [T] Use a CA8 to create the intersection between...Ch. 2.6 - [T] A spheroid is an ellipsoid with two equal...Ch. 2.6 - [T] In cartography, Earth is approximated by all...Ch. 2.6 - [T] A set 0f buzzing stunt magnets (or...Ch. 2.6 - [T] A heart-shaped surface is given by equation...Ch. 2.6 - [T] The ring torus symmetric about the z -axis is...Ch. 2.7 - Use the following ?gure as an aid in identifying...Ch. 2.7 - Use the following ?gure as an aid in identifying...Ch. 2.7 - Use the following ?gure as an aid in identifying...Ch. 2.7 - Use the following ?gure as an aid in identifying...Ch. 2.7 - For the following exercises, the rectangular...Ch. 2.7 - For the following exercises, the rectangular...Ch. 2.7 - For the following exercises, the rectangular...Ch. 2.7 - For the following exercises, the rectangular...Ch. 2.7 - For the following exercises, the equation of a...Ch. 2.7 - For the following exercises, the equation of a...Ch. 2.7 - For the following exercises, the equation of a...Ch. 2.7 - For the following exercises, the equation of a...Ch. 2.7 - For the following exercises, the equation of a...Ch. 2.7 - For the following exercises, the equation of a...Ch. 2.7 - For the following exercises, the equation of a...Ch. 2.7 - For the following exercises, the equation of a...Ch. 2.7 - For the following exercises, the equation of a...Ch. 2.7 - For the following exercises, the equation of a...Ch. 2.7 - For the following exercises, the equation of a...Ch. 2.7 - For the following exercises, the equation of a...Ch. 2.7 - For the following exercises, the equation of a...Ch. 2.7 - For the following exercises, the equation of a...Ch. 2.7 - For the following exercises, the spherical...Ch. 2.7 - For the following exercises, the spherical...Ch. 2.7 - For the following exercises, the spherical...Ch. 2.7 - For the following exercises, the spherical...Ch. 2.7 - For the following exercises, the rectangular...Ch. 2.7 - For the following exercises, the rectangular...Ch. 2.7 - For the following exercises, the rectangular...Ch. 2.7 - For the following exercises, the rectangular...Ch. 2.7 - For the following exercises, the equation of a...Ch. 2.7 - For the following exercises, the equation of a...Ch. 2.7 - For the following exercises, the equation of a...Ch. 2.7 - For the following exercises, the equation of a...Ch. 2.7 - For the following exercises, the equation of a...Ch. 2.7 - For the following exercises, the equation of a...Ch. 2.7 - For the following exercises, the equation of a...Ch. 2.7 - For the following exercises, the equation of a...Ch. 2.7 - For the following exercises, the equation of a...Ch. 2.7 - For the following exercises, the equation of a...Ch. 2.7 - For the following exercises, the cylindrical...Ch. 2.7 - For the following exercises, the cylindrical...Ch. 2.7 - For the following exercises, the cylindrical...Ch. 2.7 - For the following exercises, the cylindrical...Ch. 2.7 - For the following exercises, the spherical...Ch. 2.7 - ]For the following exercises, the spherical...Ch. 2.7 - For the following exercises, the spherical...Ch. 2.7 - For the following exercises, the spherical...Ch. 2.7 - For the following exercises, find the most...Ch. 2.7 - For the following exercises, find the most...Ch. 2.7 - For the following exercises, find the most...Ch. 2.7 - For the following exercises, find the most...Ch. 2.7 - For the following exercises, find the most...Ch. 2.7 - For the following exercises, find the most...Ch. 2.7 - For the following exercises, find the most...Ch. 2.7 - For the following exercises, find the most...Ch. 2.7 - For the following exercises, find the most...Ch. 2.7 - For the following exercises, find the most...Ch. 2.7 - For the following exercises, find the most...Ch. 2.7 - For the following exercises, find the most...Ch. 2 - For the following exercises, determine whether the...Ch. 2 - For the following exercises, determine whether the...Ch. 2 - For the following exercises, determine whether the...Ch. 2 - For the following exercises, determine whether the...Ch. 2 - For the following exercises, use the given vectors...Ch. 2 - For the following exercises, use the given vectors...Ch. 2 - For the following exercises, use the given vectors...Ch. 2 - For the following exercises, find the unit...Ch. 2 - For the following exercises, find the unit...Ch. 2 - For the following exercises, find the area or...Ch. 2 - For the following exercises, find the area or...Ch. 2 - For the following exercises, find the vector and...Ch. 2 - For the following exercises, find the vector and...Ch. 2 - For the following exercises, find the equation of...Ch. 2 - For the following exercises, find the equation of...Ch. 2 - For the following exercises, find the traces for...Ch. 2 - For the following exercises, find the traces for...Ch. 2 - For the fallowing exercises, write the given...Ch. 2 - For the fallowing exercises, write the given...Ch. 2 - For the following exercises, convert the given...Ch. 2 - For the following exercises, convert the given...Ch. 2 - For the following exercises, consider a small boat...Ch. 2 - For the following exercises, consider a small boat...Ch. 2 - An airplane is flying in the direction of 52 east...Ch. 2 - Calculate the work done by moving a particle from...Ch. 2 - The following problems consider your unsuccessful...Ch. 2 - The following problems consider your unsuccessful...
Additional Math Textbook Solutions
Find more solutions based on key concepts
Version 2 of the Chain Rule Use Version 2 of the Chain Rule to calculate the derivatives of the following funct...
Calculus: Early Transcendentals (2nd Edition)
Answer each of the following and explain your answer. a. How many lines can contain a particular segment? b. Ho...
A Problem Solving Approach To Mathematics For Elementary School Teachers (13th Edition)
25. Eye Contact In a study of facial behavior, people in a control group are timed for eye contact in a 5-minut...
Elementary Statistics (13th Edition)
TRY IT YOURSELF 1
Find the mean of the points scored by the 51 winning teams listed on page 39.
Elementary Statistics: Picturing the World (7th Edition)
Twenty five people, consisting of 15 women and 10 men are lined up in a random order. Find the probability that...
A First Course in Probability (10th Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.Similar questions
- To the Internal Revenue Service, the reasonableness of total itemized deductions depends on the taxpayer’s adjusted gross income. Large deductions, which include charity and medical deductions, are more reasonable for taxpayers with large adjusted gross incomes. If a taxpayer claims larger than average itemized deductions for a given level of income, the chances of an IRS audit are increased. Data (in thousands of dollars) on adjusted gross income and the average or reasonable amount of itemized deductions follow. Adjusted Gross Income ($1000s) Reasonable Amount ofItemized Deductions ($1000s) 22 9.6 27 9.6 32 10.1 48 11.1 65 13.5 85 17.7 120 25.5 Compute b1 and b0 (to 4 decimals).b1 b0 Complete the estimated regression equation (to 2 decimals). = + x Predict a reasonable level of total itemized deductions for a taxpayer with an adjusted gross income of $52.5 thousand (to 2 decimals). thousand dollarsWhat is the value, in dollars, of…arrow_forwardAnswer questions 8.1.10, 8.1.11and 8.1.12 respectivelyarrow_forward7.2.10 Researchers in the Hopkins Forest also count the number of maple trees (genus acer) in plots throughout the forest. The following is a histogram of the number of live maples in 1002 plots sampled over the past 20 years. The average number of maples per plot was 19.86 trees with a standard deviation of 23.65 trees. a. If we took the mean of a sample of eight plots, what would be the standard error of the mean? b. Using the central limit theorem, what is the probability that the mean of the eight would be within 1 standard error of the mean? c. Why might you think that the probability that you calculated in (b) might not be very accurate? 2. A normal population has mean 100 and variance 25. How large must the random sample be if you want the standard error of the sample average to be 1.5?arrow_forward
- Answer questions 7.3.10 and 7.3.12 respectively 7.3.12. Suppose that two independent random samples (of size n1 and n2) from two normal distributions are available. Explain how you would estimate the standard error of the difference in sample means X1 − X2 with the bootstrap method.arrow_forwardAnswer questions 7.4.6 and 7.4.7 respectivelyarrow_forwardWrite an equation for the function shown. You may assume all intercepts and asymptotes are on integers. The blue dashed lines are the asymptotes. 10 9- 8- 7 6 5 4- 3- 2 4 5 15-14-13-12-11-10 -9 -8 -7 -6 -5 -4 -3 -2 1 1 2 3 -1 -2 -3 -4 1 -5 -6- -7 -8- -9 -10+ 60 7 8 9 10 11 12 13 14 15arrow_forward
- K The mean height of women in a country (ages 20-29) is 63.7 inches. A random sample of 65 women in this age group is selected. What is the probability that the mean height for the sample is greater than 64 inches? Assume σ = 2.68. The probability that the mean height for the sample is greater than 64 inches is (Round to four decimal places as needed.)arrow_forwardAnswer questions 8.1.4, 8.1.5 and 8.1.6 respectivelyarrow_forwardAnswer questions 7.4.13, 7.4.14 and 7.4.15 respectivelyarrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Holt Mcdougal Larson Pre-algebra: Student Edition...
Algebra
ISBN:9780547587776
Author:HOLT MCDOUGAL
Publisher:HOLT MCDOUGAL
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage