Calculus Volume 3
16th Edition
ISBN: 9781938168079
Author: Gilbert Strang, Edwin Jed Herman
Publisher: OpenStax
expand_more
expand_more
format_list_bulleted
Concept explainers
Textbook Question
Chapter 2.7, Problem 363E
Use the following ?gure as an aid in identifying the relationship between the rectangular, cylindrical, and spherical
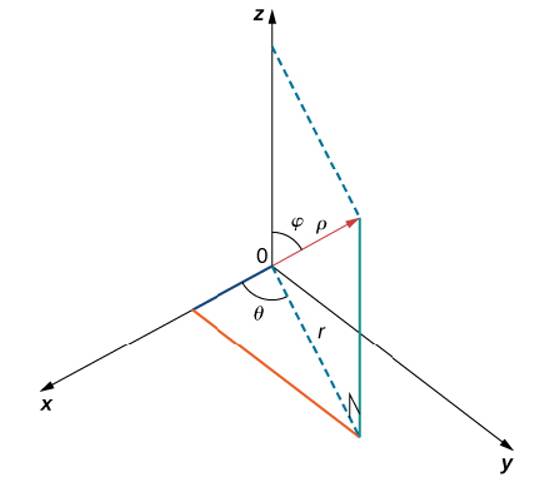
For the following exercises, the cylindrical coordinates
363.
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Find the angle
-4
4.
and
x between the vectors
2.
2.
1.
a. The points (3,-1,2) and (-1,3,-4) are the endpoints of a diameter of a sphere
i. Determine the center and radius of the sphere.
ii. Find an equation for the sphere.
b. Given the vectors a=2i-j+2 k₂ b=3i+2j-k, c =i + 2 k
i. Calculate: 2a (b-3c)
ii. Determine the vector projection of e onto b.
iii. Find the cosine of the angle between a and b.
iv. Find a unit vector that is perpendicular to the plane determined by a and e
2. Given the planes P: 2(x-1)-(y+1)-2(=-2)=0, P₂: 4x-2y + 5z =3\ and the point Q: (-2,7,4).
a. Determine whether P₁ and P₂ are parallel, coincident, perpendicular, or none of the preceding.
b. Find an equation for the plane through Q which is parallel to P₁
c. Determine scalar parametric equations for the line through Q which is parallel to the line of
intersection of P₁ and P₂
3. The position of an object at time t is given by: r(t)=e^i+e'j-t√√2k, 0≤1<0⁰
a. Determine the velocity and the speed of the object at time t
b. Determine the acceleration of the object at…
1. Consider the points in R³ given by P (-2,1,0), Q (1,-1,2), and R(-1,1,0).
Find the following:
Chapter 2 Solutions
Calculus Volume 3
Ch. 2.1 - For the following exercises, consider points...Ch. 2.1 - For the following exercises, consider points...Ch. 2.1 - For the following exercises, consider points...Ch. 2.1 - For the following exercises, consider points...Ch. 2.1 - For the following exercises, consider points...Ch. 2.1 - For the following exercises, consider points...Ch. 2.1 - For the following exercises, consider points...Ch. 2.1 - For the following exercises, consider points...Ch. 2.1 - For the following exercises, consider points...Ch. 2.1 - For the following exercises, consider points...
Ch. 2.1 - For the following exercises, consider points...Ch. 2.1 - For the following exercises, consider points...Ch. 2.1 - For the following exercises, consider points...Ch. 2.1 - For the following exercises, consider points...Ch. 2.1 - Far the following exercises, use the given...Ch. 2.1 - Far the following exercises, use the given...Ch. 2.1 - Far the following exercises, use the given...Ch. 2.1 - Far the following exercises, use the given...Ch. 2.1 - Far the following exercises, use the given...Ch. 2.1 - Far the following exercises, use the given...Ch. 2.1 - Far the following exercises, use the given...Ch. 2.1 - Far the following exercises, use the given...Ch. 2.1 - Far the following exercises, use the given...Ch. 2.1 - Far the following exercises, use the given...Ch. 2.1 - For the following exercises, find vector v with...Ch. 2.1 - For the following exercises, find vector v with...Ch. 2.1 - For the following exercises, find vector v with...Ch. 2.1 - For the following exercises, find vector v with...Ch. 2.1 - For the following exercises, find the component...Ch. 2.1 - For the following exercises, find the component...Ch. 2.1 - For the following exercises, find the component...Ch. 2.1 - For the following exercises, find the component...Ch. 2.1 - For the following exercises, find the component...Ch. 2.1 - For the following exercises, find the component...Ch. 2.1 - For the following exercises, vector u is given....Ch. 2.1 - For the following exercises, vector u is given....Ch. 2.1 - Let a=a1,a2,b=b1,b2 , and c=c1,c2 be three nonzero...Ch. 2.1 - Consider vectors a=2,4,b=1,2, and c=0 . Determine...Ch. 2.1 - Let P(x0,f(x0)) be a fixed point on the graph of...Ch. 2.1 - Consider the function f(x)=x4 , where x. Determine...Ch. 2.1 - Consider f and g two functions defined on the same...Ch. 2.1 - Find x such that vectors a=x,sinx and b=x,cosx are...Ch. 2.1 - Calculate the coordinates of point D such that...Ch. 2.1 - Consider the points A(2,1),B(10,6),C(13,4) , and...Ch. 2.1 - The speed of an object is the magnitude of its...Ch. 2.1 - A baseball player throws a baseball at an angle of...Ch. 2.1 - A bullet is fired with an initial velocity of...Ch. 2.1 - [T] A 65kg sprinter exerts a force of 798N at a 19...Ch. 2.1 - [T] Two forces, a horizontal force of 45lb and...Ch. 2.1 - [T] Two fumes, a vertical fence of 26lb and...Ch. 2.1 - [T] Three forces act an object. Two of the fences...Ch. 2.1 - Three forces with magnitudes 80lb,120lb, and 60lb...Ch. 2.1 - [T] An airplane is flying in the direction of 43...Ch. 2.1 - [T] A boat is traveling in the water at 30mph in a...Ch. 2.1 - [T] A 50-lb weight is hung by a cable so that the...Ch. 2.1 - [T] A 62-lh weight hangs from a nope that makes...Ch. 2.1 - [T] A 1500lb boat is parked on a ramp that makes...Ch. 2.1 - [T] An 85lb box is at rest on a 26 incline....Ch. 2.1 - A guy-wire supports a pole that is 75ft high. One...Ch. 2.1 - A telephone pole guy-wire has an angle of...Ch. 2.2 - Consider a rectangular box with one of the...Ch. 2.2 - Find the coordinates of point P and determine its...Ch. 2.2 - For the following exercises, describe and graph...Ch. 2.2 - For the following exercises, describe and graph...Ch. 2.2 - For the following exercises, describe and graph...Ch. 2.2 - For the following exercises, describe and graph...Ch. 2.2 - Write the equation of the plane passing through...Ch. 2.2 - Write the equation of the plane passing through...Ch. 2.2 - Find an equation of the plane passing through...Ch. 2.2 - Find an equation of the plane passing through...Ch. 2.2 - For the following exercises, find the equation of...Ch. 2.2 - For the following exercises, find the equation of...Ch. 2.2 - For the following exercises, find the equation of...Ch. 2.2 - For the following exercises, find the equation of...Ch. 2.2 - For the following exercises, find the center and...Ch. 2.2 - For the following exercises, find the center and...Ch. 2.2 - For the following exercises, express vector PQ...Ch. 2.2 - For the following exercises, express vector PQ...Ch. 2.2 - For the following exercises, express vector PQ...Ch. 2.2 - For the following exercises, express vector PQ...Ch. 2.2 - For the following exercises, express vector PQ...Ch. 2.2 - For the following exercises, express vector PQ...Ch. 2.2 - For the following exercises, use the given vectors...Ch. 2.2 - For the following exercises, use the given vectors...Ch. 2.2 - For the following exercises, use the given vectors...Ch. 2.2 - For the following exercises, use the given vectors...Ch. 2.2 - For the following exercises, vectors u and v are...Ch. 2.2 - For the following exercises, vectors u and v are...Ch. 2.2 - For the following exercises, vectors u and v are...Ch. 2.2 - For the following exercises, vectors u and v are...Ch. 2.2 - For the following exercises, find the unit vector...Ch. 2.2 - For the following exercises, find the unit vector...Ch. 2.2 - For the following exercises, find the unit vector...Ch. 2.2 - For the following exercises, find the unit vector...Ch. 2.2 - For the following exercises, find the unit vector...Ch. 2.2 - For the following exercises, find the unit vector...Ch. 2.2 - Determine whether AB and PQ are equivalent...Ch. 2.2 - Determine whether the vectors AB and PQ are...Ch. 2.2 - For the following exercises, find vector u with a...Ch. 2.2 - For the following exercises, find vector u with a...Ch. 2.2 - For the following exercises, find vector u with a...Ch. 2.2 - For the following exercises, find vector u with a...Ch. 2.2 - Determine a vector of magnitude 5 in the direction...Ch. 2.2 - Find a vector of magnitude 2 that points in the...Ch. 2.2 - Consider the points A(2,,0),B(0,1,), and C(1,1,),...Ch. 2.2 - Consider points A(,0,0),B(0,,0), and C(,,), where ...Ch. 2.2 - Let P(x,y,z) be a point situated at an equal...Ch. 2.2 - Let P(x,y,z) be a point situated at an equal...Ch. 2.2 - The points A,B, and C are collinear (in this...Ch. 2.2 - Show that points A(1,0,1),B(0,1,1) and C(1,1,1)...Ch. 2.2 - [T] A force F of 50N acts on a particle in the...Ch. 2.2 - [T] A force F of 40N acts on a box in the...Ch. 2.2 - If F is a force that moves an object from point...Ch. 2.2 - A box is pulled 4 yd horizontally in the x...Ch. 2.2 - The sum of the forces acting on an object is...Ch. 2.2 - [T] Let Fk=1,k,k2,k=1,...,n be n forces acting on...Ch. 2.2 - The force of gravity F acting on an object is...Ch. 2.2 - A 5-kg pendant chandelier is designed such that...Ch. 2.2 - [T] A 30-kg block of cement is suspended by three...Ch. 2.2 - Two soccer players are practicing for an upcoming...Ch. 2.2 - Let r(t)=x(t),y(t),z(t) be the position vector of...Ch. 2.2 - [T] Let r(t)=t,2t2,4t2 be the position vector of a...Ch. 2.3 - For the following exercises, the vectors u and v...Ch. 2.3 - For the following exercises, the vectors u and v...Ch. 2.3 - For the following exercises, the vectors u and v...Ch. 2.3 - For the following exercises, the vectors u and v...Ch. 2.3 - For the following exercises, the vectors a,b, and...Ch. 2.3 - For the following exercises, the vectors a,b, and...Ch. 2.3 - For the following exercises, the vectors a,b, and...Ch. 2.3 - For the following exercises, the vectors a,b, and...Ch. 2.3 - For the following exercises, the two-dimensional...Ch. 2.3 - For the following exercises, the two-dimensional...Ch. 2.3 - For the following exercises, the two-dimensional...Ch. 2.3 - For the following exercises, the two-dimensional...Ch. 2.3 - For the following exercises, find the measure 0f...Ch. 2.3 - For the following exercises, find the measure 0f...Ch. 2.3 - For the following exercises, find the measure 0f...Ch. 2.3 - For the following exercises, find the measure 0f...Ch. 2.3 - For the following exercises, find the measure 0f...Ch. 2.3 - For the following exercises, find the measure 0f...Ch. 2.3 - For the following exercises determine whether the...Ch. 2.3 - For the following exercises determine whether the...Ch. 2.3 - For the following exercises determine whether the...Ch. 2.3 - For the following exercises determine whether the...Ch. 2.3 - For the following exercises determine whether the...Ch. 2.3 - For the following exercises determine whether the...Ch. 2.3 - For the following exercises determine whether the...Ch. 2.3 - For the following exercises determine whether the...Ch. 2.3 - For the following exercises determine whether the...Ch. 2.3 - For the following exercises determine whether the...Ch. 2.3 - [T] Consider the points P(4,5) and Q(5,7) ....Ch. 2.3 - [T] Consider points A(1,1),B(2,7) , and C(6,3)....Ch. 2.3 - Determine the measure of angle A in triangle ABC ,...Ch. 2.3 - Consider points P(3,7,2) and Q(1,1,3). Determine...Ch. 2.3 - For the following exercises, determine which (if...Ch. 2.3 - For the following exercises, determine which (if...Ch. 2.3 - For the following exercises, determine which (if...Ch. 2.3 - For the following exercises, determine which (if...Ch. 2.3 - For the following exercises, determine which (if...Ch. 2.3 - For the following exercises, determine which (if...Ch. 2.3 - For the following problems, the vector u is given....Ch. 2.3 - For the following problems, the vector u is given....Ch. 2.3 - For the following problems, the vector u is given....Ch. 2.3 - For the following problems, the vector u is given....Ch. 2.3 - For the following problems, the vector u is given....Ch. 2.3 - For the following problems, the vector u is given....Ch. 2.3 - For the following exercises, the vectors u and v...Ch. 2.3 - For the following exercises, the vectors u and v...Ch. 2.3 - For the following exercises, the vectors u and v...Ch. 2.3 - For the following exercises, the vectors u and v...Ch. 2.3 - For the following exercises, the vectors u and v...Ch. 2.3 - For the following exercises, the vectors u and v...Ch. 2.3 - A methane molecule has a carbon atom situated at...Ch. 2.3 - [T] Find the vectors that join the center of a...Ch. 2.3 - Find the work done by force F=5,6,2 (measured in...Ch. 2.3 - [T] A sled is pulled by exerting a force of 100N...Ch. 2.3 - [T] A father is pulling his son on a sled at an...Ch. 2.3 - [T] A car is towed using a force of 1600N . The...Ch. 2.3 - [T] A boat sails north aided by a wind blowing in...Ch. 2.3 - Vector p=150,225,375 represents the price of...Ch. 2.3 - [T] Two forces F1 and F2 are represented by...Ch. 2.3 - [T] Consider r(t)=cost,sint,2t the position vector...Ch. 2.4 - For the following exercises, the vectors u and v...Ch. 2.4 - For the following exercises, the vectors u and v...Ch. 2.4 - For the following exercises, the vectors u and v...Ch. 2.4 - For the following exercises, the vectors u and v...Ch. 2.4 - `For the following exercises, the vectors u and v...Ch. 2.4 - For the following exercises, the vectors u and v...Ch. 2.4 - In the following exercises, vectors u and v are...Ch. 2.4 - In the following exercises, vectors u and v are...Ch. 2.4 - In the following exercises, vectors u and v are...Ch. 2.4 - In the following exercises, vectors u and v are...Ch. 2.4 - In the following exercises, vectors u and v are...Ch. 2.4 - In the following exercises, vectors u and v are...Ch. 2.4 - In the following exercises, vectors u and v are...Ch. 2.4 - In the following exercises, vectors u and v are...Ch. 2.4 - Calculate the determinant |ijk117203| .Ch. 2.4 - Calculate the determinant |ijk034161| .Ch. 2.4 - For the following exercises, the vector u and v...Ch. 2.4 - For the following exercises, the vector u and v...Ch. 2.4 - Find vector (a2b)c , where...Ch. 2.4 - Find vector c(a+3b) , where...Ch. 2.4 - [T] Use the cross product uv to find the acute...Ch. 2.4 - [T] Use the cross product uv to find the obtuse...Ch. 2.4 - Use the sine and cosine of the angle between two...Ch. 2.4 - Verify Lagrange’s identity uv2=u2v2(uv)2 for...Ch. 2.4 - Nonzero vectors u and v are called collinear if...Ch. 2.4 - Nonzero vectors u and v are called collinear if...Ch. 2.4 - Find the area of the parallelogram with adjacent...Ch. 2.4 - Find the area of the parallelogram with adjacent...Ch. 2.4 - Consider paints A(3,1,2),B(2,1,5), and C(1,2,2)....Ch. 2.4 - Consider points A(2,3,4),B(0,1,2), and C(1,2,0)....Ch. 2.4 - In the following exercises, vectors u,v, and w are...Ch. 2.4 - In the following exercises, vectors u,v, and w are...Ch. 2.4 - In the following exercises, vectors u,v, and w are...Ch. 2.4 - In the following exercises, vectors u,v, and w are...Ch. 2.4 - Find vectors a,b, and c with a triple scalar...Ch. 2.4 - The triple scalar product of vector a,b, and c is...Ch. 2.4 - Consider the parallelepiped with edges OA,OB, and...Ch. 2.4 - Consider points A(,0,0),B(0,,0), and C(0,0,), with...Ch. 2.4 - Let u,v, and w be three-dimensional vectors and c...Ch. 2.4 - Show that vectors u=1,0,8,v=0,1,6, and w=1,9,3...Ch. 2.4 - Nonzero vectors u,v, and w are said to be linearly...Ch. 2.4 - Consider vectors u=1,4,7,v=2,1,4,w=0,9,18, and...Ch. 2.4 - Consider points A(0,0,2),B(1,0,2),C(1,1,2), and...Ch. 2.4 - Show that vectors i+j,ij, and i+j+k are linearly...Ch. 2.4 - Let u=u1,u2,0 and v=v1,v2,0, be two-dimensional...Ch. 2.4 - Consider points P(2,1),Q(4,2) and R(1,2). Find the...Ch. 2.4 - Determine a vector of magnitude 10 perpendicular...Ch. 2.4 - Determine a unit vector perpendicular to the plane...Ch. 2.4 - Consider u and v two three-dimensional vectors. If...Ch. 2.4 - [T] Assume that the magnitudes of two nonzero...Ch. 2.4 - Find all vectors w=w1,w2,w3 that satisfy the...Ch. 2.4 - - Solve the w1,0,1=3,0,3, where w=w1,w2,w3 is a...Ch. 2.4 - [T] A mechanic uses a 12in . wrench to turn a...Ch. 2.4 - [T] A boy applies the brakes on a bicycle by...Ch. 2.4 - [T] Find the magnitude of the force that needs to...Ch. 2.4 - [T] What is the magnitude of the force required to...Ch. 2.4 - [T] The fence vector F acting on a proton with all...Ch. 2.4 - [T] The fence vector F acting on a proton with an...Ch. 2.4 - [T] Consider r(t)=cost,sint,2t the position vector...Ch. 2.4 - A solar panel is mounted 011 the roof of a house....Ch. 2.5 - Figure 2.73 Industrial pipe installations often...Ch. 2.5 - Figure 2.73 Industrial pipe installations often...Ch. 2.5 - Figure 2.73 Industrial pipe installations often...Ch. 2.5 - Figure 2.73 Industrial pipe installations often...Ch. 2.5 - Figure 2.73 Industrial pipe installations often...Ch. 2.5 - Figure 2.73 Industrial pipe installations often...Ch. 2.5 - Figure 2.73 Industrial pipe installations often...Ch. 2.5 - Figure 2.73 Industrial pipe installations often...Ch. 2.5 - Figure 2.73 Industrial pipe installations often...Ch. 2.5 - In the following exercises, points P and Q are...Ch. 2.5 - In the following exercises, points P and Q are...Ch. 2.5 - In the following exercises, points P and Q are...Ch. 2.5 - In the following exercises, points P and Q are...Ch. 2.5 - For the following exercises, point P and vector v...Ch. 2.5 - For the following exercises, point P and vector v...Ch. 2.5 - For the following exercises, point P and vector v...Ch. 2.5 - For the following exercises, point P and vector v...Ch. 2.5 - For the following exercises, line L is given. Find...Ch. 2.5 - For the following exercises, line L is given. Find...Ch. 2.5 - For the following exercises, line L is given. Find...Ch. 2.5 - For the following exercises, line L is given. Find...Ch. 2.5 - For the following exercises, lines L1 and L2 are...Ch. 2.5 - For the following exercises, lines L1 and L2 are...Ch. 2.5 - For the following exercises, lines L1 and L2 are...Ch. 2.5 - For the following exercises, lines L1 and L2 are...Ch. 2.5 - For the following exercises, lines L1 and L2 are...Ch. 2.5 - For the following exercises, lines L1 and L2 are...Ch. 2.5 - For the following exercises, Lines L1 and L2 are...Ch. 2.5 - For the following exercises, Lines L1 and L2 are...Ch. 2.5 - For the following exercises, Lines L1 and L2 are...Ch. 2.5 - For the following exercises, Lines L1 and L2 are...Ch. 2.5 - For the following exercises, Lines L1 and L2 are...Ch. 2.5 - For the following exercises, Lines L1 and L2 are...Ch. 2.5 - For the following exercises, point P and vector n...Ch. 2.5 - For the following exercises, point P and vector n...Ch. 2.5 - For the following exercises, point P and vector n...Ch. 2.5 - For the following exercises, point P and vector n...Ch. 2.5 - For the following exercises, the equation of a...Ch. 2.5 - For the following exercises, the equation of a...Ch. 2.5 - For the following exercises, the equation of a...Ch. 2.5 - For the following exercises, the equation of a...Ch. 2.5 - Given paint P(1,2,3) and vector n=i+j , find point...Ch. 2.5 - Show there is no plane perpendicular to n=i+j that...Ch. 2.5 - Find parametric equations 0f the Line passing...Ch. 2.5 - Find symmetric equations of the line passing...Ch. 2.5 - Show that line x12=y+13=z24 is parallel to plane...Ch. 2.5 - Find the real number such that the line of...Ch. 2.5 - For the following exercises, points P,Q, and R are...Ch. 2.5 - For the following exercises, points P,Q, and R are...Ch. 2.5 - Consider the planes of equations x+y+z=1 and x+z=0...Ch. 2.5 - Consider the planes of equations y+z2=0 and xy=0 ....Ch. 2.5 - Find the scalar equation of the plane that passes...Ch. 2.5 - Find the general equation of the plane that passes...Ch. 2.5 - Determine whether the Line of parametric equations...Ch. 2.5 - Determine whether the Line of parametric equations...Ch. 2.5 - Find the distance from point P(1,5,4) to the plane...Ch. 2.5 - Find the distance from point P(1,2,3) to the plane...Ch. 2.5 - For the following exercises, the equations of two...Ch. 2.5 - For the following exercises, the equations of two...Ch. 2.5 - For the following exercises, the equations of two...Ch. 2.5 - For the following exercises, the equations of two...Ch. 2.5 - Show that the lines of equations x=t,y=1+t,z=2+t,t...Ch. 2.5 - Show that the lines of equations...Ch. 2.5 - Consider point C(3,2,4) and the plane of equation...Ch. 2.5 - Consider the plane of equation xyz8=0. Find the...Ch. 2.5 - Two children are playing with a ball. The girl...Ch. 2.5 - [T] John allocates d dollars to consume monthly...Ch. 2.5 - [T] Consider r(t)=sint,cost,2t the position vector...Ch. 2.5 - [T] A solar panel is mounted on the roof of a...Ch. 2.6 - For the following exercises, sketch and describe...Ch. 2.6 - For the following exercises, sketch and describe...Ch. 2.6 - For the following exercises, sketch and describe...Ch. 2.6 - For the following exercises, sketch and describe...Ch. 2.6 - For the following exercises, sketch and describe...Ch. 2.6 - For the following exercises, sketch and describe...Ch. 2.6 - For the following exercises, the graph of a...Ch. 2.6 - For the following exercises, the graph of a...Ch. 2.6 - For the following exercises, the graph of a...Ch. 2.6 - For the following exercises, the graph of a...Ch. 2.6 - For the fallowing exercises, match the given...Ch. 2.6 - For the fallowing exercises, match the given...Ch. 2.6 - For the fallowing exercises, match the given...Ch. 2.6 - For the fallowing exercises, match the given...Ch. 2.6 - For the fallowing exercises, match the given...Ch. 2.6 - For the fallowing exercises, match the given...Ch. 2.6 - For the following exercises, rewrite the given...Ch. 2.6 - For the following exercises, rewrite the given...Ch. 2.6 - For the following exercises, rewrite the given...Ch. 2.6 - For the following exercises, rewrite the given...Ch. 2.6 - For the following exercises, rewrite the given...Ch. 2.6 - For the following exercises, rewrite the given...Ch. 2.6 - For the following exercises, rewrite the given...Ch. 2.6 - For the following exercises, rewrite the given...Ch. 2.6 - For the following exercises, rewrite the given...Ch. 2.6 - For the following exercises, rewrite the given...Ch. 2.6 - For the following exercises, rewrite the given...Ch. 2.6 - For the following exercises, rewrite the given...Ch. 2.6 - For the following exercises, find the trace of the...Ch. 2.6 - For the following exercises, find the trace of the...Ch. 2.6 - For the following exercises, find the trace of the...Ch. 2.6 - For the following exercises, find the trace of the...Ch. 2.6 - For the following exercises, find the trace of the...Ch. 2.6 - For the following exercises, find the trace of the...Ch. 2.6 - Use the graph of the given quadric surface to...Ch. 2.6 - Use the graph of the given quadric surface to...Ch. 2.6 - For the following exercises, the equation of a...Ch. 2.6 - For the following exercises, the equation of a...Ch. 2.6 - For the following exercises, the equation of a...Ch. 2.6 - For the following exercises, the equation of a...Ch. 2.6 - For the following exercises, the equation of a...Ch. 2.6 - For the following exercises, the equation of a...Ch. 2.6 - Write the standard form of the equation of the...Ch. 2.6 - Write the standard form of the equation of the...Ch. 2.6 - Determine the intersection points of elliptic cone...Ch. 2.6 - Determine the intersection points of parabolic...Ch. 2.6 - Find the equation of the quadric surface with...Ch. 2.6 - Find the equation of the quadric surface with...Ch. 2.6 - If the surface of a parabolic reflector is...Ch. 2.6 - Consider the parabolic reflector described by...Ch. 2.6 - Show that quadric surface...Ch. 2.6 - Show that quadric surface x2+y2+z22xy+2yz1=0...Ch. 2.6 - [T] The intersection between cylinder (x1)2+y2=1...Ch. 2.6 - Hyperboloid of one sheet 25x2+25y2z2=25 and...Ch. 2.6 - [T] Use a CA8 to create the intersection between...Ch. 2.6 - [T] A spheroid is an ellipsoid with two equal...Ch. 2.6 - [T] In cartography, Earth is approximated by all...Ch. 2.6 - [T] A set 0f buzzing stunt magnets (or...Ch. 2.6 - [T] A heart-shaped surface is given by equation...Ch. 2.6 - [T] The ring torus symmetric about the z -axis is...Ch. 2.7 - Use the following ?gure as an aid in identifying...Ch. 2.7 - Use the following ?gure as an aid in identifying...Ch. 2.7 - Use the following ?gure as an aid in identifying...Ch. 2.7 - Use the following ?gure as an aid in identifying...Ch. 2.7 - For the following exercises, the rectangular...Ch. 2.7 - For the following exercises, the rectangular...Ch. 2.7 - For the following exercises, the rectangular...Ch. 2.7 - For the following exercises, the rectangular...Ch. 2.7 - For the following exercises, the equation of a...Ch. 2.7 - For the following exercises, the equation of a...Ch. 2.7 - For the following exercises, the equation of a...Ch. 2.7 - For the following exercises, the equation of a...Ch. 2.7 - For the following exercises, the equation of a...Ch. 2.7 - For the following exercises, the equation of a...Ch. 2.7 - For the following exercises, the equation of a...Ch. 2.7 - For the following exercises, the equation of a...Ch. 2.7 - For the following exercises, the equation of a...Ch. 2.7 - For the following exercises, the equation of a...Ch. 2.7 - For the following exercises, the equation of a...Ch. 2.7 - For the following exercises, the equation of a...Ch. 2.7 - For the following exercises, the equation of a...Ch. 2.7 - For the following exercises, the equation of a...Ch. 2.7 - For the following exercises, the spherical...Ch. 2.7 - For the following exercises, the spherical...Ch. 2.7 - For the following exercises, the spherical...Ch. 2.7 - For the following exercises, the spherical...Ch. 2.7 - For the following exercises, the rectangular...Ch. 2.7 - For the following exercises, the rectangular...Ch. 2.7 - For the following exercises, the rectangular...Ch. 2.7 - For the following exercises, the rectangular...Ch. 2.7 - For the following exercises, the equation of a...Ch. 2.7 - For the following exercises, the equation of a...Ch. 2.7 - For the following exercises, the equation of a...Ch. 2.7 - For the following exercises, the equation of a...Ch. 2.7 - For the following exercises, the equation of a...Ch. 2.7 - For the following exercises, the equation of a...Ch. 2.7 - For the following exercises, the equation of a...Ch. 2.7 - For the following exercises, the equation of a...Ch. 2.7 - For the following exercises, the equation of a...Ch. 2.7 - For the following exercises, the equation of a...Ch. 2.7 - For the following exercises, the cylindrical...Ch. 2.7 - For the following exercises, the cylindrical...Ch. 2.7 - For the following exercises, the cylindrical...Ch. 2.7 - For the following exercises, the cylindrical...Ch. 2.7 - For the following exercises, the spherical...Ch. 2.7 - ]For the following exercises, the spherical...Ch. 2.7 - For the following exercises, the spherical...Ch. 2.7 - For the following exercises, the spherical...Ch. 2.7 - For the following exercises, find the most...Ch. 2.7 - For the following exercises, find the most...Ch. 2.7 - For the following exercises, find the most...Ch. 2.7 - For the following exercises, find the most...Ch. 2.7 - For the following exercises, find the most...Ch. 2.7 - For the following exercises, find the most...Ch. 2.7 - For the following exercises, find the most...Ch. 2.7 - For the following exercises, find the most...Ch. 2.7 - For the following exercises, find the most...Ch. 2.7 - For the following exercises, find the most...Ch. 2.7 - For the following exercises, find the most...Ch. 2.7 - For the following exercises, find the most...Ch. 2 - For the following exercises, determine whether the...Ch. 2 - For the following exercises, determine whether the...Ch. 2 - For the following exercises, determine whether the...Ch. 2 - For the following exercises, determine whether the...Ch. 2 - For the following exercises, use the given vectors...Ch. 2 - For the following exercises, use the given vectors...Ch. 2 - For the following exercises, use the given vectors...Ch. 2 - For the following exercises, find the unit...Ch. 2 - For the following exercises, find the unit...Ch. 2 - For the following exercises, find the area or...Ch. 2 - For the following exercises, find the area or...Ch. 2 - For the following exercises, find the vector and...Ch. 2 - For the following exercises, find the vector and...Ch. 2 - For the following exercises, find the equation of...Ch. 2 - For the following exercises, find the equation of...Ch. 2 - For the following exercises, find the traces for...Ch. 2 - For the following exercises, find the traces for...Ch. 2 - For the fallowing exercises, write the given...Ch. 2 - For the fallowing exercises, write the given...Ch. 2 - For the following exercises, convert the given...Ch. 2 - For the following exercises, convert the given...Ch. 2 - For the following exercises, consider a small boat...Ch. 2 - For the following exercises, consider a small boat...Ch. 2 - An airplane is flying in the direction of 52 east...Ch. 2 - Calculate the work done by moving a particle from...Ch. 2 - The following problems consider your unsuccessful...Ch. 2 - The following problems consider your unsuccessful...
Additional Math Textbook Solutions
Find more solutions based on key concepts
Version 2 of the Chain Rule Use Version 2 of the Chain Rule to calculate the derivatives of the following funct...
Calculus: Early Transcendentals (2nd Edition)
Answer each of the following and explain your answer. a. How many lines can contain a particular segment? b. Ho...
A Problem Solving Approach To Mathematics For Elementary School Teachers (13th Edition)
25. Eye Contact In a study of facial behavior, people in a control group are timed for eye contact in a 5-minut...
Elementary Statistics (13th Edition)
TRY IT YOURSELF 1
Find the mean of the points scored by the 51 winning teams listed on page 39.
Elementary Statistics: Picturing the World (7th Edition)
Twenty five people, consisting of 15 women and 10 men are lined up in a random order. Find the probability that...
A First Course in Probability (10th Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.Similar questions
- ved by user Last Modified: 41m ago ▾ es Mailings Review View Table Design Get Add-ins Online Comment My Add-ins - Videos Add-ins Media Comments Triangle ABC is shown in the xy -coordinate plane. y The triangle will be rotated 180° clockwise around the point (3, 4) to create AA'B'C'. Which characteristics of AA'B'C' will be the same for the corresponding characteristics of AABC? Select all that apply. A. the coordinates of A B. the coordinates of B C. the perimeter of AA'B'C' D. the area of AA'B'C' E. the measure of B F. the length of segment A'B' 1) The degree measure of each exterior angle of a regular octagon OF HH 83° Reuse Files euse Files 1) O W Wikipedia Help Picture Format Link Bookmark Cross-reference Links Kromal Layout Header Footer Page Num Header & Farrow_forwardI need to rotate the shape in the third quadrant 90° counterclockwise. Where would my triple prime figure be in the fourth quadrant?arrow_forwardHow do you find the focus and the directrix of a Prabola?arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
Holt Mcdougal Larson Pre-algebra: Student Edition...
Algebra
ISBN:9780547587776
Author:HOLT MCDOUGAL
Publisher:HOLT MCDOUGAL