Chapter 20, Problem 20.65QP

Interpretation Introduction

Interpretation: For the given nuclear reaction, X should be identified and the equation should be balanced.

Concept Introduction:

• Nuclear reaction can be written in the shorthand notation with the parentheses. Bombarding particle, that is projectile can be represented as first symbol in the parentheses and the emitted particle that is ejectile which can be represented as the second particle in the parentheses.

Parent nucleus and daughter nucleus can be represented in the front part of the parentheses and back part of the parentheses respectively.

$\begin{array}{l}{}_7{N}^{15}\left(p,\alpha \right){}_6{C}^{12}\\ Parentnucleus\left(Projectile,ejectile\right)Daughternucleus\end{array}$

• On accordance with law of conservation of mass, for any chemical reaction, total masses of reactants and products must be equal.

To find: The value of X in the given nuclear equation (a).

Answer to Problem 20.65QP

$\begin{array}{l}\text{(a)}\\ {\text{ U}}_{\text{92}}^{\text{235}}{\text{+n}}_{\text{0}}^{\text{1}}\stackrel{}{\to }{\text{Ba}}_{\text{56}}^{\text{140}}{\text{+3n}}_{\text{0}}^{\text{1}}\text{+}\underset{\_}{{\text{Kr}}_{\text{36}}^{\text{93}}}\text{ X=}\underset{\_}{{\text{Kr}}_{\text{36}}^{\text{93}}}\\ \text{(b)}\\ {\text{ U}}_{\text{92}}^{\text{235}}{\text{+n}}_{\text{0}}^{\text{1}}\stackrel{}{\to }{\text{Cs}}_{\text{55}}^{\text{144}}{\text{+Rb}}_{\text{37}}^{\text{90}}\text{+}\underset{\_}{{\text{2n}}_{\text{0}}^{\text{1}}}\text{ X=}\underset{\_}{{\text{2n}}_{\text{0}}^{\text{1}}}\\ \text{(c)}\\ {\text{ U}}_{\text{92}}^{\text{235}}{\text{+n}}_{\text{0}}^{\text{1}}\stackrel{}{\to }{\text{Br}}_{\text{35}}^{\text{87}}\text{+}\underset{\_}{{\text{La}}_{\text{57}}^{\text{146}}}{\text{+3n}}_{\text{0}}^{\text{1}}\text{ X=}\underset{\_}{{\text{La}}_{\text{57}}^{\text{146}}}\\ \text{(d)}\\ {\text{ U}}_{\text{92}}^{\text{235}}{\text{+n}}_{\text{0}}^{\text{1}}\stackrel{}{\to }{\text{Sm}}_{\text{62}}^{\text{160}}{\text{+Zn}}_{\text{30}}^{\text{72}}\text{+}\underset{\_}{{\text{4n}}_{\text{0}}^{\text{1}}}\text{ X=}\underset{\_}{{\text{4n}}_{\text{0}}^{\text{1}}}\end{array}$

$\text{X=}\underset{\_}{{\text{Kr}}_{\text{36}}^{\text{93}}}$

Explanation of Solution

Explanation

Nuclear reaction can be written in the shorthand notation with the parentheses. Bombarding particle, that is projectile can be represented as first symbol in the parentheses and the emitted particle that is ejectile which can be represented as the second particle in the parentheses. Parent nucleus and daughter nucleus can be represented in the front part of the parentheses and back part of the parentheses respectively. So for any nuclear reaction, short hand notation will be in this form that is, $\begin{array}{l}\\ \\ \text{Parent}\text{nucleus}\left(\text{Projectile,}\text{ejectile}\right)\text{Daughter}\text{nucleus}\end{array}$

For the given reaction a, Short hand notation is ${\text{U}}_{\text{92}}^{\text{235}}\left(\text{n,n}\right)\text{X}$. From the notation it is clear that,

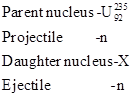
The given chemical equation can be written as,

${\text{U}}_{\text{92}}^{\text{235}}{\text{+n}}_{\text{0}}^{\text{1}}\stackrel{}{\to }{\text{Ba}}_{\text{56}}^{\text{140}}{\text{+3n}}_{\text{0}}^{\text{1}}\text{+}$ X

On accordance with law of conservation of mass, for any chemical reaction, total masses of reactants and products must be equal. So the X will be ${}_{\text{36}}^{93}\text{X}$. By analyzing the X, atomic number of X is 36 and the atomic mass is 93. So it is found that X is ${\text{Kr}}_{\text{36}}^{\text{93}}$.

 So the balanced equation can be written as,

${\text{U}}_{\text{92}}^{\text{235}}{\text{+n}}_{\text{0}}^{\text{1}}\stackrel{}{\to }{\text{Ba}}_{\text{56}}^{\text{140}}{\text{+3n}}_{\text{0}}^{\text{1}}\text{+}\underset{\_}{{\text{Kr}}_{\text{36}}^{\text{93}}}$

Find the value of X in the given nuclear equation (b)

$\text{X=}\underset{\_}{{\text{2n}}_{\text{0}}^{\text{1}}}$

For the given reaction b, Shorthand notation is ${\text{U}}_{\text{92}}^{\text{235}}\left({\text{n}}_0^1{\text{,Cs}}_{55}^{144}\right)\text{X}$. From the notation it is clear that,

$\begin{array}{l}\text{Parent}\text{nucleus}\text{-}{\text{U}}_{\text{92}}^{\text{235}}\\ \text{Projectile}{\text{-n}}^{\text{1}}{}_{\text{0}}\\ \text{Daughter}{\text{nucleus-Cs}}_{\text{55}}^{\text{144}}\\ \text{Ejectile}\text{-}\text{X}\end{array}$

The given chemical equation can be written as,

${\text{U}}_{\text{92}}^{\text{235}}{\text{+n}}_{\text{0}}^{\text{1}}\stackrel{}{\to }{\text{Cs}}_{\text{55}}^{\text{144}}{\text{+Rb}}_{\text{37}}^{\text{90}}\text{+}$ X

On accordance with law of conservation of mass, for any chemical reaction, total masses of reactants and products must be equal. So the X will be ${}_0^1\text{2X}$. By analyzing the X, atomic number of X is 0 and the atomic mass is 1. It is found that $\text{X=}\underset{\_}{{\text{2n}}_{\text{0}}^{\text{1}}}$.

 So the balanced equation can be written as,

${\text{U}}_{\text{92}}^{\text{235}}{\text{+n}}_{\text{0}}^{\text{1}}\stackrel{}{\to }{\text{Cs}}_{\text{55}}^{\text{144}}{\text{+Rb}}_{\text{37}}^{\text{90}}\text{+}\underset{\_}{{\text{2n}}_{\text{0}}^{\text{1}}}$

Find the value of X in the given nuclear equation (c).

For the given reactions, Shorthand notation is ${\text{U}}_{92}^{235}\left(\text{n,n}\right)\text{X}$. From the notation it is clear that,

$\begin{array}{l}\text{Parent}\text{nucleus}{\text{-U}}_{92}^{235}\\ \text{Projectile}{\text{- }}^{\text{1}}{}_{\text{0}}\text{n}\\ \text{Daughter}\text{nucleus-X}\\ \text{Ejectile}\text{-}{}^{\text{1}}{}_{\text{0}}\text{n}\end{array}$

The given chemical equation can be written as,

${\text{U}}_{\text{92}}^{\text{235}}{\text{+n}}_{\text{0}}^{\text{1}}\stackrel{}{\to }{\text{Br}}_{\text{35}}^{\text{87}}\text{+}$ X+ ${\text{3n}}_{\text{0}}^{\text{1}}$

On accordance with law of conservation of mass, for any chemical reaction, total masses of reactants and products must be equal. So X will be ${}_{57}^{146}\text{X}$. By analyzing the X, atomic number of X is57 and the atomic mass is 146. So it should be the isotope of lanthanum. It is found that $\text{X=}\underset{\_}{{\text{La}}_{\text{57}}^{\text{146}}}$

 So the balanced equation can be written as,

${\text{U}}_{\text{92}}^{\text{235}}{\text{+n}}_{\text{0}}^{\text{1}}\stackrel{}{\to }{\text{Br}}_{\text{35}}^{\text{87}}\text{+}\underset{\_}{{\text{La}}_{\text{57}}^{\text{146}}}{\text{+3n}}_{\text{0}}^{\text{1}}$

Find the value of X in the given nuclear equation (d).

For the given reactions, Shorthand notation is ${\text{U}}_{92}^{235}\left(\text{n,n}\right)\text{X}$. From the notation it is clear that,

$\begin{array}{l}\text{Parent}\text{nucleus}{\text{-U}}_{92}^{235}\\ \text{Projectile}{\text{- }}^{\text{1}}{}_{\text{0}}\text{n}\\ \text{Daughter}\text{nucleus-X}\\ \text{Ejectile}\text{-}{}^{\text{1}}{}_{\text{0}}\text{n}\end{array}$

The given chemical equation can be written as,

${\text{U}}_{\text{92}}^{\text{235}}{\text{+n}}_{\text{0}}^{\text{1}}\stackrel{}{\to }{\text{Sm}}_{\text{62}}^{\text{160}}{\text{+Zn}}_{\text{30}}^{\text{72}}\text{+}$ X

On accordance with law of conservation of mass, for any chemical reaction, total masses of reactants and products must be equal. So X will be ${}_0^1\text{4X}$. By analyzing the X, atomic number of X is0 and the atomic mass is 1. It is found that $\text{X=}\underset{\_}{{\text{4n}}_{\text{0}}^{\text{1}}}$

 So the balanced equation can be written as,

${\text{U}}_{\text{92}}^{\text{235}}{\text{+n}}_{\text{0}}^{\text{1}}\stackrel{}{\to }{\text{Sm}}_{\text{62}}^{\text{160}}{\text{+Zn}}_{\text{30}}^{\text{72}}\text{+}\underset{\_}{{\text{4n}}_{\text{0}}^{\text{1}}}$

Conclusion

For the given nuclear reaction, X is identified and the equation is balanced.