Student Solutions Manual for Basic Business Statistics
13th Edition
ISBN: 9780321926708
Author: David M. Levine; Mark L. Berenson; Timothy C. Krehbiel; Kathryn A. Szabat; David F. Stephan
Publisher: Pearson Education
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 20, Problem 1PS
For this problem, use the following payoff table:
a. Construct an opportunity loss table.
b. Construct a decision tree.
a.
Expert Solution
To determine
Make an opportunity table using the given payoff table.
Explanation of Solution
The payoff table is given.
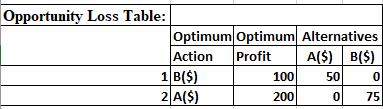
Use Excel to construct an opportunity loss table.
Software procedure:
The step-by-step procedure to make an opportunity loss table is given below.
Select Add-Ins > PHStat > Decision-Making > Opportunity Loss.
In the opportunity loss dialog, fill Number of Events as 2 and Number of Alternative Actions as 2.
Click OK.
In the template generated by Excel, fill the payoff table as given in the problem.
The excel output for opportunity loss table is shown below.
b.
Expert Solution
To determine
Construct a decision tree for the given payoff table.
Explanation of Solution
The tree diagram for the given payoff table is given below.
Want to see more full solutions like this?
Subscribe now to access step-by-step solutions to millions of textbook problems written by subject matter experts!
Students have asked these similar questions
A well-known company predominantly makes flat pack furniture for students. Variability with the automated machinery means the wood components are cut with a standard deviation in length of 0.45 mm. After they are cut the components are measured. If their length is more than 1.2 mm from the required length, the components are rejected.
a) Calculate the percentage of components that get rejected.
b) In a manufacturing run of 1000 units, how many are expected to be rejected?
c) The company wishes to install more accurate equipment in order to reduce the rejection rate by one-half, using the same ±1.2mm rejection criterion. Calculate the maximum acceptable standard deviation of the new process.
5. Let X and Y be independent random variables and let the superscripts denote
symmetrization (recall Sect. 3.6). Show that
(X + Y) X+ys.
8. Suppose that the moments of the random variable X are constant, that is, suppose
that EX" =c for all n ≥ 1, for some constant c. Find the distribution of X.
Chapter 20 Solutions
Student Solutions Manual for Basic Business Statistics
Ch. 20 - For this problem, use the following payoff table:...Ch. 20 - Prob. 2PSCh. 20 - Prob. 3PSCh. 20 - Prob. 4PSCh. 20 - Prob. 5PSCh. 20 - For the following payoff table, the probability of...Ch. 20 - Prob. 7PSCh. 20 - Prob. 8PSCh. 20 - Prob. 9PSCh. 20 - Prob. 10PS
Ch. 20 - Prob. 11PSCh. 20 - A vendor at a local baseball stadium must...Ch. 20 - The Islander Fishing Company purchases clams for...Ch. 20 - Prob. 14PSCh. 20 - In Problem 20.3, you developed a payoff table for...Ch. 20 - In Problem 20.4, you developed a payoff table to...Ch. 20 - In Problem 20.5, you developed a payoff table for...Ch. 20 - Prob. 18PSCh. 20 - Prob. 19PSCh. 20 - 1n Problem 20.12, a vendor at a baseball stadium...Ch. 20 - In Problem 20.14. an investor is trying to...Ch. 20 - In Problem 20.16. an author is deciding which of...Ch. 20 - Prob. 23PSCh. 20 - Prob. 24PSCh. 20 - Prob. 25PSCh. 20 - Prob. 26PSCh. 20 - Prob. 27PSCh. 20 - Prob. 28PSCh. 20 - Prob. 29PSCh. 20 - Prob. 30PSCh. 20 - Prob. 31PSCh. 20 - Prob. 32PSCh. 20 - How is Bayes’ theorem used to revise...Ch. 20 - Prob. 34PSCh. 20 - Prob. 35PSCh. 20 - A supermarket chain purchases large quantities of...Ch. 20 - The owner of a company that supplies home heating...Ch. 20 - The manufacturer of a nationally distributed brand...Ch. 20 - An entrepreneur wants to determine whether it...Ch. 20 - A manufacturer of a brand of inexpensive felt-tip...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, statistics and related others by exploring similar questions and additional content below.Similar questions
- 9. The concentration function of a random variable X is defined as Qx(h) = sup P(x ≤ X ≤x+h), h>0. Show that, if X and Y are independent random variables, then Qx+y (h) min{Qx(h). Qr (h)).arrow_forward10. Prove that, if (t)=1+0(12) as asf->> O is a characteristic function, then p = 1.arrow_forward9. The concentration function of a random variable X is defined as Qx(h) sup P(x ≤x≤x+h), h>0. (b) Is it true that Qx(ah) =aQx (h)?arrow_forward
- 3. Let X1, X2,..., X, be independent, Exp(1)-distributed random variables, and set V₁₁ = max Xk and W₁ = X₁+x+x+ Isk≤narrow_forward7. Consider the function (t)=(1+|t|)e, ER. (a) Prove that is a characteristic function. (b) Prove that the corresponding distribution is absolutely continuous. (c) Prove, departing from itself, that the distribution has finite mean and variance. (d) Prove, without computation, that the mean equals 0. (e) Compute the density.arrow_forward1. Show, by using characteristic, or moment generating functions, that if fx(x) = ½ex, -∞0 < x < ∞, then XY₁ - Y2, where Y₁ and Y2 are independent, exponentially distributed random variables.arrow_forward
- 1. Show, by using characteristic, or moment generating functions, that if 1 fx(x): x) = ½exarrow_forward1990) 02-02 50% mesob berceus +7 What's the probability of getting more than 1 head on 10 flips of a fair coin?arrow_forward9. The concentration function of a random variable X is defined as Qx(h) sup P(x≤x≤x+h), h>0. = x (a) Show that Qx+b(h) = Qx(h).arrow_forward
- Suppose that you buy a lottery ticket, and you have to pick six numbers from 1 through 50 (repetitions allowed). Which combination is more likely to win: 13, 48, 17, 22, 6, 39 or 1, 2, 3, 4, 5, 6? barrow_forward2 Make a histogram from this data set of test scores: 72, 79, 81, 80, 63, 62, 89, 99, 50, 78, 87, 97, 55, 69, 97, 87, 88, 99, 76, 78, 65, 77, 88, 90, and 81. Would a pie chart be appropriate for this data? ganizing Quantitative Data: Charts and Graphs 45arrow_forward10 Meteorologists use computer models to predict when and where a hurricane will hit shore. Suppose they predict that hurricane Stat has a 20 percent chance of hitting the East Coast. a. On what info are the meteorologists basing this prediction? b. Why is this prediction harder to make than your chance of getting a head on your next coin toss? U anoiaarrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Glencoe Algebra 1, Student Edition, 9780079039897...
Algebra
ISBN:9780079039897
Author:Carter
Publisher:McGraw Hill
Introduction to Integers,Maths - What are integers - English; Author: Mathispower4u;https://www.youtube.com/watch?v=04pURxo-iu0;License: Standard YouTube License, CC-BY
Integers-Middle School Math; Author: MooMooMath and Science;https://www.youtube.com/watch?v=DGWcWtqM_yk;License: Standard YouTube License, CC-BY