Student Solutions Manual for Basic Business Statistics
13th Edition
ISBN: 9780321926708
Author: David M. Levine; Mark L. Berenson; Timothy C. Krehbiel; Kathryn A. Szabat; David F. Stephan
Publisher: Pearson Education
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 20, Problem 12PS
A vendor at a local baseball stadium must determine whether to sell ice cream or soft drinks at today’s game. The vendor believes that the profit made will depend on the weather. The payoff table (in
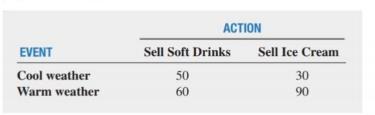
Based on her past experience at this time of year, the vendor estimates the
a. Determine the optimal action based on the maximax criterion.
b. Determine the optimal action based on the maximax criterion.
c. Compute the expected monetary value (EMV) for selling soft drinks and selling ice cream.
d. Compute the expected opportunity loss (EOL) for selling soft drinks and selling ice cream.
e. Explain the meaning of the
f. Based on the results of (c) or (d), which would you choose to sell. soft drinks or ice cream? Why?
g. Compute the coefficient of variation for selling soft drinks and selling ice cream.
h. Compute the return-to-risk ratio (RTRR) for selling soft drinks and selling ice cream.
i. Based on (g) and (h). what would you choose to sell, soft drinks or ice cream? Why?
j. Compare the results of (f) and (i) and explain any differences.
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Please provide the solution for the attached image in detailed.
20 km, because
GISS
Worksheet 10
Jesse runs a small business selling and delivering mealie meal to the spaza shops.
He charges a fixed rate of R80, 00 for delivery and then R15, 50 for each packet of
mealle meal he delivers. The table below helps him to calculate what to charge
his customers.
10
20
30
40
50
Packets of mealie
meal (m)
Total costs in Rands
80
235
390
545
700
855
(c)
10.1.
Define the following terms:
10.1.1. Independent Variables
10.1.2. Dependent Variables
10.2.
10.3.
10.4.
10.5.
Determine the independent and dependent variables.
Are the variables in this scenario discrete or continuous values? Explain
What shape do you expect the graph to be? Why?
Draw a graph on the graph provided to represent the information in the
table above.
TOTAL COST OF PACKETS OF MEALIE MEAL
900
800
700
600
COST (R)
500
400
300
200
100
0
10
20
30
40
60
NUMBER OF PACKETS OF MEALIE MEAL
Let X be a random variable with support SX = {−3, 0.5, 3, −2.5, 3.5}. Part ofits probability mass function (PMF) is given bypX(−3) = 0.15, pX(−2.5) = 0.3, pX(3) = 0.2, pX(3.5) = 0.15.(a) Find pX(0.5).(b) Find the cumulative distribution function (CDF), FX(x), of X.1(c) Sketch the graph of FX(x).
Chapter 20 Solutions
Student Solutions Manual for Basic Business Statistics
Ch. 20 - For this problem, use the following payoff table:...Ch. 20 - Prob. 2PSCh. 20 - Prob. 3PSCh. 20 - Prob. 4PSCh. 20 - Prob. 5PSCh. 20 - For the following payoff table, the probability of...Ch. 20 - Prob. 7PSCh. 20 - Prob. 8PSCh. 20 - Prob. 9PSCh. 20 - Prob. 10PS
Ch. 20 - Prob. 11PSCh. 20 - A vendor at a local baseball stadium must...Ch. 20 - The Islander Fishing Company purchases clams for...Ch. 20 - Prob. 14PSCh. 20 - In Problem 20.3, you developed a payoff table for...Ch. 20 - In Problem 20.4, you developed a payoff table to...Ch. 20 - In Problem 20.5, you developed a payoff table for...Ch. 20 - Prob. 18PSCh. 20 - Prob. 19PSCh. 20 - 1n Problem 20.12, a vendor at a baseball stadium...Ch. 20 - In Problem 20.14. an investor is trying to...Ch. 20 - In Problem 20.16. an author is deciding which of...Ch. 20 - Prob. 23PSCh. 20 - Prob. 24PSCh. 20 - Prob. 25PSCh. 20 - Prob. 26PSCh. 20 - Prob. 27PSCh. 20 - Prob. 28PSCh. 20 - Prob. 29PSCh. 20 - Prob. 30PSCh. 20 - Prob. 31PSCh. 20 - Prob. 32PSCh. 20 - How is Bayes’ theorem used to revise...Ch. 20 - Prob. 34PSCh. 20 - Prob. 35PSCh. 20 - A supermarket chain purchases large quantities of...Ch. 20 - The owner of a company that supplies home heating...Ch. 20 - The manufacturer of a nationally distributed brand...Ch. 20 - An entrepreneur wants to determine whether it...Ch. 20 - A manufacturer of a brand of inexpensive felt-tip...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, statistics and related others by exploring similar questions and additional content below.Similar questions
- A well-known company predominantly makes flat pack furniture for students. Variability with the automated machinery means the wood components are cut with a standard deviation in length of 0.45 mm. After they are cut the components are measured. If their length is more than 1.2 mm from the required length, the components are rejected. a) Calculate the percentage of components that get rejected. b) In a manufacturing run of 1000 units, how many are expected to be rejected? c) The company wishes to install more accurate equipment in order to reduce the rejection rate by one-half, using the same ±1.2mm rejection criterion. Calculate the maximum acceptable standard deviation of the new process.arrow_forward5. Let X and Y be independent random variables and let the superscripts denote symmetrization (recall Sect. 3.6). Show that (X + Y) X+ys.arrow_forward8. Suppose that the moments of the random variable X are constant, that is, suppose that EX" =c for all n ≥ 1, for some constant c. Find the distribution of X.arrow_forward
- 9. The concentration function of a random variable X is defined as Qx(h) = sup P(x ≤ X ≤x+h), h>0. Show that, if X and Y are independent random variables, then Qx+y (h) min{Qx(h). Qr (h)).arrow_forward10. Prove that, if (t)=1+0(12) as asf->> O is a characteristic function, then p = 1.arrow_forward9. The concentration function of a random variable X is defined as Qx(h) sup P(x ≤x≤x+h), h>0. (b) Is it true that Qx(ah) =aQx (h)?arrow_forward
- 3. Let X1, X2,..., X, be independent, Exp(1)-distributed random variables, and set V₁₁ = max Xk and W₁ = X₁+x+x+ Isk≤narrow_forward7. Consider the function (t)=(1+|t|)e, ER. (a) Prove that is a characteristic function. (b) Prove that the corresponding distribution is absolutely continuous. (c) Prove, departing from itself, that the distribution has finite mean and variance. (d) Prove, without computation, that the mean equals 0. (e) Compute the density.arrow_forward1. Show, by using characteristic, or moment generating functions, that if fx(x) = ½ex, -∞0 < x < ∞, then XY₁ - Y2, where Y₁ and Y2 are independent, exponentially distributed random variables.arrow_forward
- 1. Show, by using characteristic, or moment generating functions, that if 1 fx(x): x) = ½exarrow_forward1990) 02-02 50% mesob berceus +7 What's the probability of getting more than 1 head on 10 flips of a fair coin?arrow_forward9. The concentration function of a random variable X is defined as Qx(h) sup P(x≤x≤x+h), h>0. = x (a) Show that Qx+b(h) = Qx(h).arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Glencoe Algebra 1, Student Edition, 9780079039897...
Algebra
ISBN:9780079039897
Author:Carter
Publisher:McGraw Hill
Holt Mcdougal Larson Pre-algebra: Student Edition...
Algebra
ISBN:9780547587776
Author:HOLT MCDOUGAL
Publisher:HOLT MCDOUGAL
Solve ANY Optimization Problem in 5 Steps w/ Examples. What are they and How do you solve them?; Author: Ace Tutors;https://www.youtube.com/watch?v=BfOSKc_sncg;License: Standard YouTube License, CC-BY
Types of solution in LPP|Basic|Multiple solution|Unbounded|Infeasible|GTU|Special case of LP problem; Author: Mechanical Engineering Management;https://www.youtube.com/watch?v=F-D2WICq8Sk;License: Standard YouTube License, CC-BY
Optimization Problems in Calculus; Author: Professor Dave Explains;https://www.youtube.com/watch?v=q1U6AmIa_uQ;License: Standard YouTube License, CC-BY
Introduction to Optimization; Author: Math with Dr. Claire;https://www.youtube.com/watch?v=YLzgYm2tN8E;License: Standard YouTube License, CC-BY