Chapter 2, Problem 51P

Obtain the equivalent resistance at the terminals a-b for each of the circuits in Fig. 2.115.

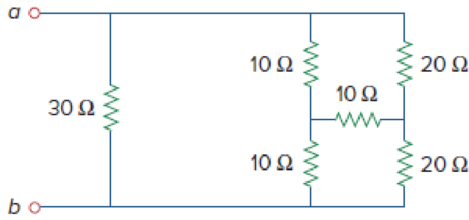
Figure 2.115

To determine

Calculate the equivalent resistance at terminals a-b in Figure 2.115(a).

Answer to Problem 51P

The equivalent resistance at terminals a-b in Figure 2.115(a) is $\underset{\_}{9.23\Omega }$.

Explanation of Solution

Formula used:

Consider the following delta to wye conversion, when all branches in a delta consists same value.

$R_{\text{Y}}=\frac{R_{\Delta }}{3}$ (1)

Consider the expression for $N$ resistors connected in parallel.

$\frac{1}{R_{\text{eq}}}=\frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{R_3}+\cdots +\frac{1}{R_N}$

Here,

$R_1,R_2,R_3\cdots R_N$ are resistors.

Consider the expression for $N$ resistors connected in series.

$R_{\text{eq}}=R_1+R_2+R_3+\cdots +R_N$

Calculation:

Refer to Figure 2.115(a) in the textbook For Prob.2.51.

Step 1:

In Figure 2.115(a), convert the wye connection into delta connection.

Substitute $10\Omega$ for $R_{\text{Y}}$ in equation (1) to obtain the branch values of delta.

$\begin{array}{c}{R}_{\Delta }=3\left(10\Omega \right)\\ =30\Omega \end{array}$

Since all branches values are same in a wye connection that is $R_1=R_2=R_3=10\Omega$ , therefore all branches of delta will be same that is $R_a=R_b=R_c=30\Omega$.

Modify Figure 2.115(a) as shown in Figure 1.

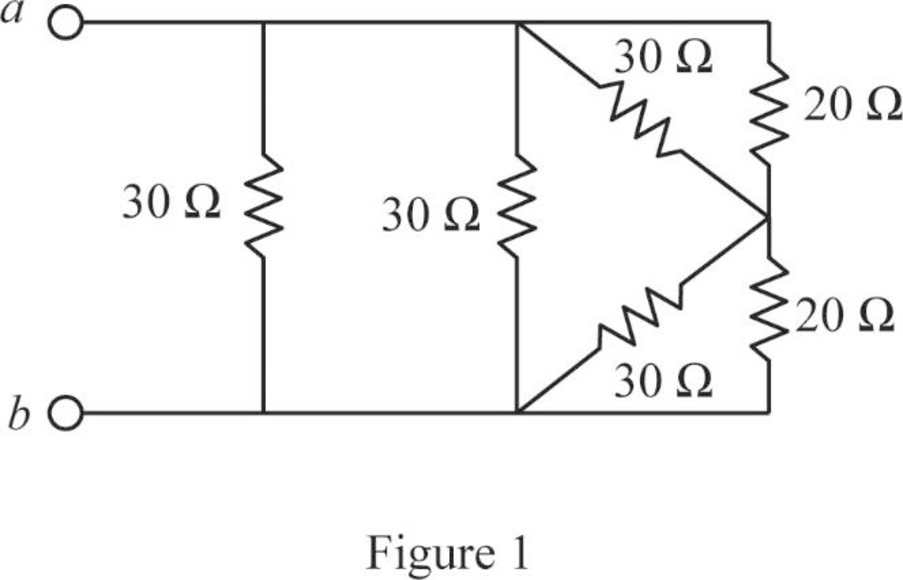
Step 2:

In Figure 1, as $30\Omega \text{and}20\Omega$ are connected in parallel, therefore the equivalent resistance of parallel connected circuit is calculated as follows.

$\begin{array}{c}{R}_{\text{eq1}}=\frac{1}{\left(\frac{1}{30\Omega }+\frac{1}{20\Omega }\right)}\\ =\frac{1}{\left(\frac{2+3}{60\Omega }\right)}\\ =\frac{60\Omega }{5}\\ =12\Omega \end{array}$

Step 3:

In Figure 1, as $30\Omega \text{and}30\Omega$ are connected in parallel, therefore the equivalent resistance of parallel connected circuit is calculated as follows.

$\begin{array}{c}{R}_{\text{eq2}}=\frac{1}{\left(\frac{1}{30\Omega }+\frac{1}{30\Omega }\right)}\\ =\frac{1}{\left(\frac{1+1}{30\Omega }\right)}\\ =\frac{30\Omega }{2}\\ =15\Omega \end{array}$

Step 4:

In Figure 1, as $30\Omega \text{and}20\Omega$ are connected in parallel, therefore the equivalent resistance of parallel connected circuit is calculated as follows.

$\begin{array}{c}{R}_{\text{eq3}}=\frac{1}{\left(\frac{1}{30\Omega }+\frac{1}{20\Omega }\right)}\\ =\frac{1}{\left(\frac{2+3}{60\Omega }\right)}\\ =\frac{60\Omega }{5}\\ =12\Omega \end{array}$

Modify Figure 1 as shown in Figure 2.

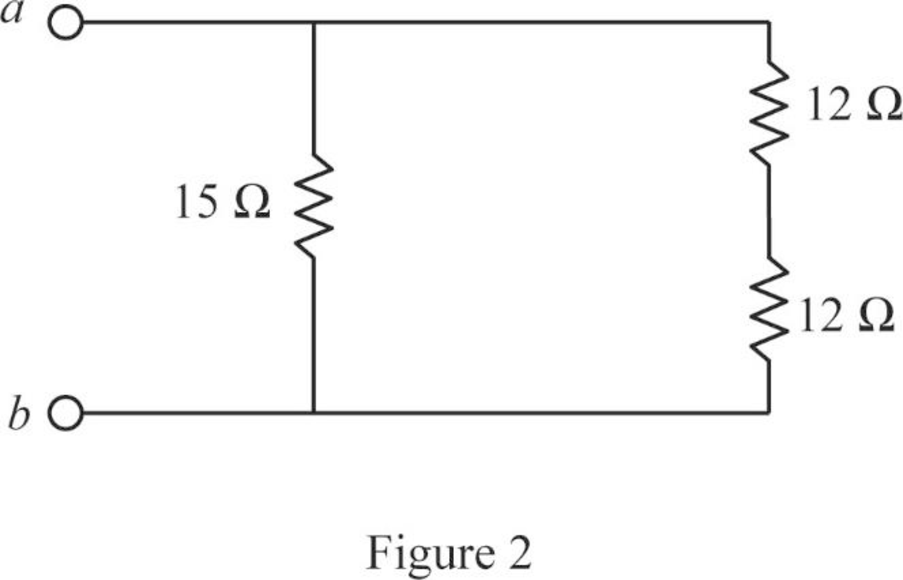
Step 5:

In Figure 2, as two $12\Omega$ resistors are connected in series, therefore the equivalent resistance of the series connected circuit is calculated as follows.

$\begin{array}{c}{R}_{\text{eq}4}=12\Omega +12\Omega \\ =24\Omega \end{array}$

Modify Figure 2 as shown in Figure 3.

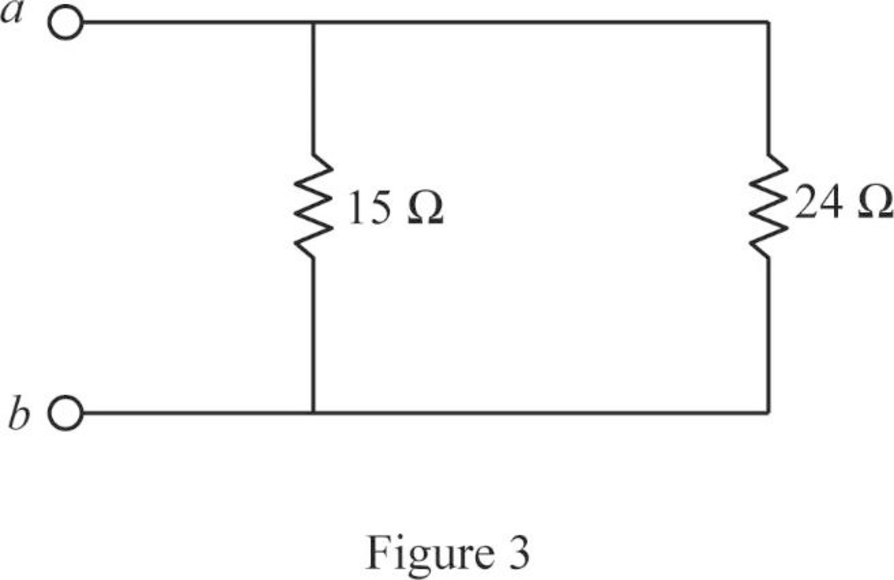
Step 6:

In Figure 3, as $15\Omega \text{and}24\Omega$ are connected in parallel, therefore the equivalent resistance of parallel connected circuit is calculated as follows.

$\begin{array}{c}{R}_{ab(a)}=\frac{1}{\left(\frac{1}{15\Omega }+\frac{1}{24\Omega }\right)}\\ =\frac{1}{\left(\frac{8+5}{120\Omega }\right)}\\ =\frac{120\Omega }{13}\\ =9.23\Omega \end{array}$

Conclusion:

Thus, the equivalent resistor at terminals a-b in Figure 2.115(a) is $\underset{\_}{9.23\Omega }$.

To determine

Calculate the equivalent resistance at terminals a-b in Figure 2.115(b).

Answer to Problem 51P

The equivalent resistance at terminals a-b in Figure 2.115(b) is $\underset{\_}{36.25\Omega }$.

Explanation of Solution

Formula used:

Consider the wye to delta conversions.

$R_a=\frac{R_1{R}_2+R_2{R}_3+R_3{R}_1}{R_1}$ (2)

$R_b=\frac{R_1{R}_2+R_2{R}_3+R_3{R}_1}{R_2}$ (3)

$R_c=\frac{R_1{R}_2+R_2{R}_3+R_3{R}_1}{R_3}$ (4)

Here,

$R_1,R_2,R_3,R_a,R_b,R_c$ are resistors.

Calculation:

Refer to Figure 2.115(b) in the textbook For Prob.2.51.

Step 1:

In Figure 2.115(a), convert the wye connection $\left(10\Omega ,20\Omega \text{and}5\Omega \right)$ into delta connection.

Consider $R_1=10\Omega$, $R_2=20\Omega$ and $R_3=5\Omega$.

Substitute $10\Omega$ for $R_1$, $20\Omega$ for $R_2$ and $5\Omega$ for $R_3$ in equation (2) to obtain $R_a$ value of delta connection.

$\begin{array}{c}{R}_a=\frac{\left(10\Omega \right)\left(20\Omega \right)+\left(20\Omega \right)\left(5\Omega \right)+\left(5\Omega \right)\left(10\Omega \right)}{10\Omega }\\ =\frac{200+100+50}{10\Omega }\Omega \\ =\frac{350}{10}\Omega \\ =35\Omega \end{array}$

Substitute $10\Omega$ for $R_1$, $20\Omega$ for $R_2$ and $5\Omega$ for $R_3$ in equation (3) to obtain $R_b$ value of delta connection.

$\begin{array}{c}{R}_b=\frac{\left(10\Omega \right)\left(20\Omega \right)+\left(20\Omega \right)\left(5\Omega \right)+\left(5\Omega \right)\left(10\Omega \right)}{20\Omega }\\ =\frac{200+100+50}{20\Omega }\Omega \\ =\frac{350}{20}\Omega \\ =17.5\Omega \end{array}$

Substitute $10\Omega$ for $R_1$, $20\Omega$ for $R_2$ and $5\Omega$ for $R_3$ in equation (3) to obtain $R_c$ value of delta connection.

$\begin{array}{c}{R}_c=\frac{\left(10\Omega \right)\left(20\Omega \right)+\left(20\Omega \right)\left(5\Omega \right)+\left(5\Omega \right)\left(10\Omega \right)}{5\Omega }\\ =\frac{200+100+50}{5\Omega }\Omega \\ =\frac{350}{5}\Omega \\ =70\Omega \end{array}$

Modify Figure 2.115(b) as shown in Figure 4.

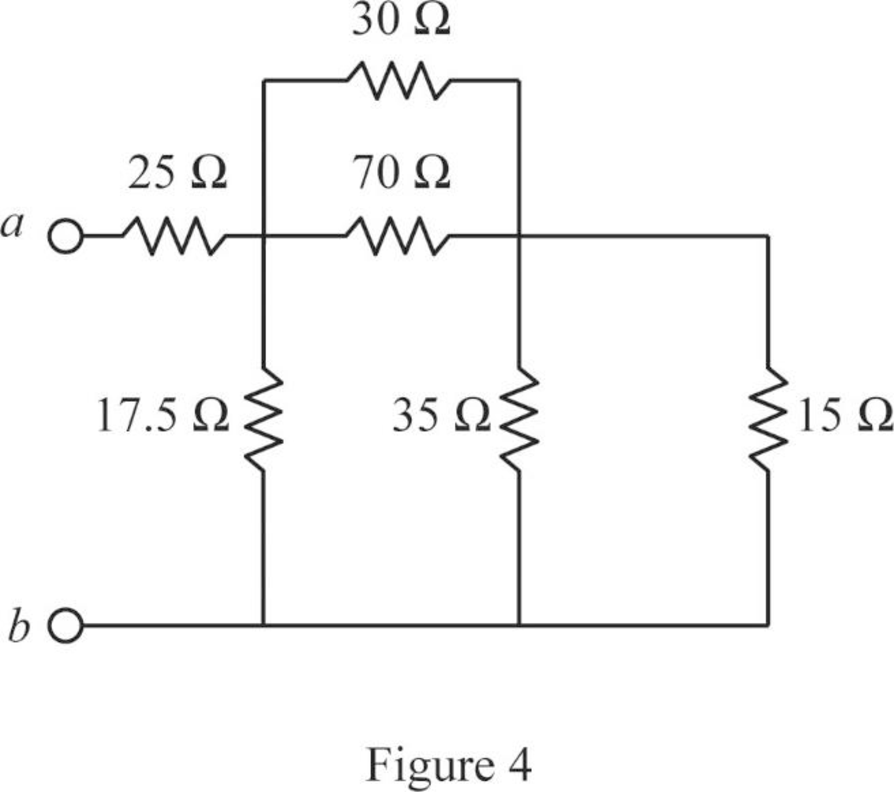
Step 2:

In Figure 4, as $30\Omega \text{and}70\Omega$ are connected in parallel, therefore the equivalent resistance of parallel connected circuit is calculated as follows.

$\begin{array}{c}{R}_{\text{eq1}}=\frac{1}{\left(\frac{1}{30\Omega }+\frac{1}{70\Omega }\right)}\\ =\frac{1}{\left(\frac{7+3}{210\Omega }\right)}\\ =\frac{210\Omega }{10}\\ =21\Omega \end{array}$

Step 3:

In Figure 4, as $35\Omega \text{and}15\Omega$ are connected in parallel, therefore the equivalent resistance of parallel connected circuit is calculated as follows.

$\begin{array}{c}{R}_{\text{eq2}}=\frac{1}{\left(\frac{1}{35\Omega }+\frac{1}{15\Omega }\right)}\\ =\frac{1}{\left(\frac{3+7}{105\Omega }\right)}\\ =\frac{105\Omega }{10}\\ =10.5\Omega \end{array}$

Modify Figure 4 as shown in Figure 5.

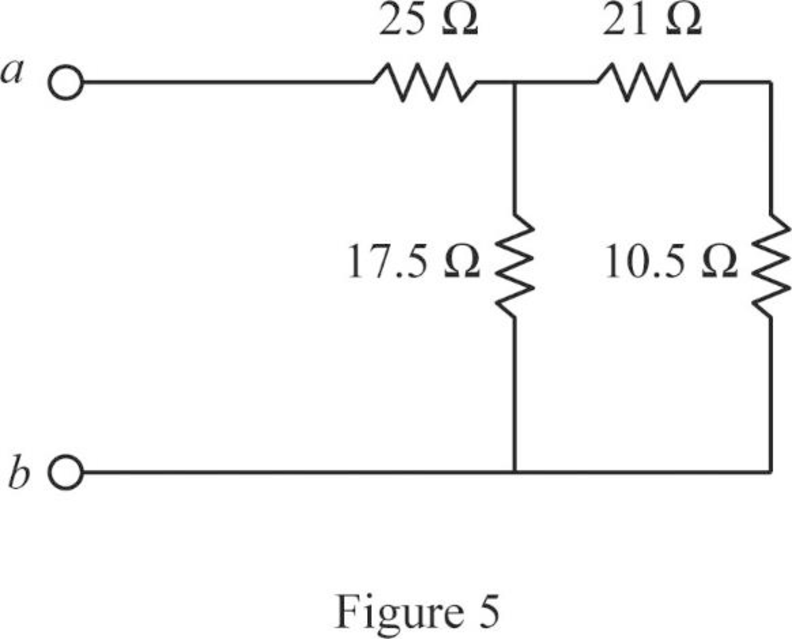
Step 4:

In Figure 5, as $21\Omega \text{and}10.5\Omega$ resistors are connected in series, therefore the equivalent resistance of the series connected circuit is calculated as follows.

$\begin{array}{c}{R}_{\text{eq}3}=21\Omega +10.5\Omega \\ =31.5\Omega \end{array}$

Modify Figure 5 as shown in Figure 6.

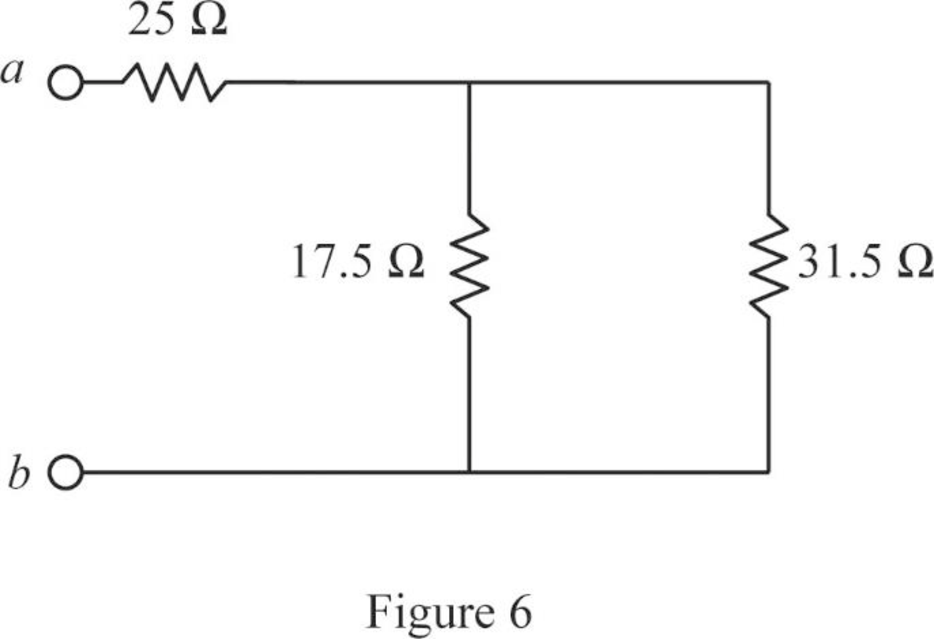
Step 5:

In Figure 6, as $17.5\Omega \text{and}31.5\Omega$ are connected in parallel, that are again connected in series with $25\Omega$ resistor, therefore the equivalent resistance at terminals a-b is calculated as follows.

$\begin{array}{c}{R}_{ab\left(b\right)}=25\Omega +\frac{1}{\left(\frac{1}{17.5\Omega }+\frac{1}{31.5\Omega }\right)}\\ =25\Omega +\left(11.25\right)\Omega \\ =36.25\Omega \end{array}$

Conclusion:

Thus, the equivalent resistor at terminals a-b in Figure 2.115(b) is $\underset{\_}{36.25\Omega }$.