College Physics (10th Edition)
10th Edition
ISBN: 9780321902788
Author: Hugh D. Young, Philip W. Adams, Raymond Joseph Chastain
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 2, Problem 51P
ǁ That’s a lot of hot air! A hot-air balloonist, rising vertically with a constant speed of 5.00 m/s, releases a sandbag at the instant the balloon is 40.0 m above the ground. (See Figure 2.54) After it is released, the sandbag encounters no appreciable air drag. (a) Compute the position and velocity of the sandbag at 0.250 s and 1.00 s after its release. (b) How many seconds after its release will the bag strike the ground? (c) How fast is it moving as it strikes the ground? (d) What is the greatest height above the ground that the sandbag reaches? (e) Sketch graphs of this bag’s acceleration, velocity, and vertical position as functions of time.
Figure 2.54
Problem 51
Expert Solution & Answer
Trending nowThis is a popular solution!
Learn your wayIncludes step-by-step video
schedule10:17
Students have asked these similar questions
two satellites are in circular orbits around the Earth. Satellite A is at an altitude equal to the Earth's radius, while satellite B is at an altitude equal to twice the Earth's radius. What is the ratio of their periods, Tb/Ta
Fresnel lens: You would like to design a 25 mm diameter blazed Fresnel zone plate with a first-order power of
+1.5 diopters. What is the lithography requirement (resolution required) for making this lens that is designed
for 550 nm? Express your answer in units of μm to one decimal point.
Fresnel lens: What would the power of the first diffracted order of this lens be at wavelength of 400 nm?
Express your answer in diopters to one decimal point.
Eye: A person with myopic eyes has a far point of 15 cm. What power contact lenses does she need to correct
her version to a standard far point at infinity? Give your answer in diopter to one decimal point.
Paraxial design of a field flattener. Imagine your optical system has Petzal curvature of the field with radius
p. In Module 1 of Course 1, a homework problem asked you to derive the paraxial focus shift along the axis
when a slab of glass was inserted in a converging cone of rays. Find or re-derive that result, then use it to
calculate the paraxial radius of curvature of a field flattener of refractive index n that will correct the observed
Petzval. Assume that the side of the flattener facing the image plane is plano. What is the required radius of
the plano-convex field flattener? (p written as rho )
Chapter 2 Solutions
College Physics (10th Edition)
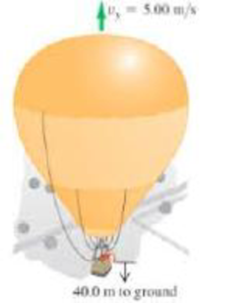
Ch. 2 - A jogger runs due east along a straight jogging...Ch. 2 - Give an example or two in which the magnitude of...Ch. 2 - Under what conditions is average velocity equal to...Ch. 2 - If an automobile is traveling north, can it have...Ch. 2 - True or false? (a) If an objects average speed is...Ch. 2 - Is it possible for an object to be accelerating...Ch. 2 - A wind-up toy car is released from rest. It...Ch. 2 - Can an object with constant acceleration reverse...Ch. 2 - If the graph of the position of an object as a...Ch. 2 - If the graph of the position of an object as a...
Ch. 2 - If the graph of the velocity of an object as a...Ch. 2 - Figure 2.31 shows graphs of the positions of three...Ch. 2 - Figure 2.32 shows graphs of the velocities of...Ch. 2 - Figure 2.33 shows the graph of an objects position...Ch. 2 - Figure 2.3 shows the graph of an objects velocity...Ch. 2 - Figure 2.35 shows the position x of an object as a...Ch. 2 - Figure 2.36 shows the velocity of an object Ux as...Ch. 2 - A ball is dropped from rest from the top of a...Ch. 2 - Which of the following statements about average...Ch. 2 - A ball is thrown directly upward with a velocity...Ch. 2 - Two objects start at the same place at the same...Ch. 2 - An object starts from rest and accelerates...Ch. 2 - If a car moving at 80 mi/h takes 400 ft to stop...Ch. 2 - Figure 2.38 shows the velocity of a jogger as a...Ch. 2 - A certain airport runway of length L allows planes...Ch. 2 - A ball rolls off a horizontal shelf a height h...Ch. 2 - A frog leaps vertically into the air and...Ch. 2 - A cat runs in a straight line. Figure 2.39 shows a...Ch. 2 - A wildebeest is running in a straight line, which...Ch. 2 - A bullet is dropped into a river from a very high...Ch. 2 - An ant is crawling along a straight wire, which we...Ch. 2 - || A person is walking briskly in a straight line,...Ch. 2 - A dog runs from points A to B to C in 3.0 s. (See...Ch. 2 - || BIO Figure 2.44 shows the position of a moving...Ch. 2 - || An object moves along the x axis. Figure 2.45...Ch. 2 - || A boulder starting from rest rolls down a hill...Ch. 2 - || Each graph in Figure 2.47 shows the position of...Ch. 2 - Family trip. You and your family take a trip to...Ch. 2 - Hypersonic scramjet. On March 27, 2004, the United...Ch. 2 - Plate tectonics. The earths crust is broken up...Ch. 2 - A runner covers one lap of a circular track 40.0 m...Ch. 2 - At room temperature, sound travels at a speed of...Ch. 2 - BIO Ouch! Nerve impulses travel at different...Ch. 2 - While riding on a bus traveling down the highway,...Ch. 2 - || A mouse travels along a straight line; its...Ch. 2 - || The freeway blues! When you normally drive the...Ch. 2 - ||Two runners start simultaneously at opposite...Ch. 2 - || A physics professor leaves her house and walks...Ch. 2 - || A test car travels in a straight line along the...Ch. 2 - || Figure 2.50 shows the position x of a crawling...Ch. 2 - || The graph in Figure 2.51 shows the velocity of...Ch. 2 - || DATA A test driver at Incredible Motors, Inc.,...Ch. 2 - (a) The pilot of a jet fighter will black out at...Ch. 2 - || For each graph of velocity as a function of...Ch. 2 - || A little cat, Bella, walks along a straight...Ch. 2 - The driver of a car traveling on the highway...Ch. 2 - BIO Animal motion. Cheetahs, the fastest of the...Ch. 2 - || BIO A cat drops from a shelf 4.0 ft above the...Ch. 2 - || BIO Blackout? A jet fighter pilot wishes to...Ch. 2 - A car is traveling at 60 mi/h down a highway. (a)...Ch. 2 - BIO If a pilot accelerates at more than 4g, he...Ch. 2 - || BIO Air-bag injuries. During an auto accident,...Ch. 2 - Starting from rest, a boulder rolls down a hill...Ch. 2 - Faster than a speeding bullet! The Beretta Model...Ch. 2 - Electric drag racer. An electric drag racer is...Ch. 2 - The reaction time of the average automobile driver...Ch. 2 - According to recent typical test data, a Ford...Ch. 2 - A car sitting at a red light begins to accelerate...Ch. 2 - If the radius of a circle of area A and...Ch. 2 - In the redesign of a machine, a metal cubical part...Ch. 2 - You have two cylindrical tanks. The tank with the...Ch. 2 - Prob. 42PCh. 2 - Two rockets having the same acceleration start...Ch. 2 - The drivers of two cars having equal speeds hit...Ch. 2 - Two bicyclists start a sprint from rest, each...Ch. 2 - (a) If a flea can jump straight up to a height of...Ch. 2 - A brick is released with no initial speed from the...Ch. 2 - Worlds tallest building. Suppose that you drop a...Ch. 2 - A tennis ball on Mars, where the acceleration due...Ch. 2 - Measuring g. One way to measure g on another...Ch. 2 - Thats a lot of hot air! A hot-air balloonist,...Ch. 2 - Astronauts on the moon. Astronauts on our moon...Ch. 2 - A student throws a water balloon vertically...Ch. 2 - A rock is thrown vertically upward with a speed of...Ch. 2 - BIO Physiological effects of large acceleration....Ch. 2 - Two stones are thrown vertically upward from the...Ch. 2 - Two coconuts fall freely from rest at the same...Ch. 2 - A Toyota Prius driving north at 65 mi/h and a VW...Ch. 2 - You are driving eastbound on the interstate at 70...Ch. 2 - A helicopter 8.50 m above the ground and...Ch. 2 - || A jetliner has a cruising air speed of 600 mi/h...Ch. 2 - || At the instant the traffic light turns green,...Ch. 2 - || A state trooper is traveling down the...Ch. 2 - Two rocks are thrown directly upward with the same...Ch. 2 - BIO Prevention of hip fractures. Falls resulting...Ch. 2 - || Egg drop. You are on the roof of the physics...Ch. 2 - || Galileos marbles. Galileo used marbles rolling...Ch. 2 - A large boulder is ejected vertically upward from...Ch. 2 - A car is traveling in the negative x direction at...Ch. 2 - Bio A healthy heart pumping at a rate of 72 beats...Ch. 2 - A car in the northbound lane s sitting at a red...Ch. 2 - A rocket blasts off vertically from rest on the...Ch. 2 - BIO An elite human sorinter reaches his top speed...Ch. 2 - || How high is the cliff? Suppose you are climbing...Ch. 2 - BIO Blood flow in the heart. The human circulatory...Ch. 2 - BIO Blood flow in the heart. The human circulatory...Ch. 2 - BIO Blood flow in the heart. The human circulatory...
Additional Science Textbook Solutions
Find more solutions based on key concepts
Plants use the process of photosynthesis to convert the energy in sunlight to chemical energy in the form of su...
Campbell Essential Biology (7th Edition)
1. Rub your hands together vigorously. What happens? Discuss the energy transfers and transformations that take...
College Physics: A Strategic Approach (3rd Edition)
Police Captain Jeffers has suffered a myocardial infarction. a. Explain to his (nonmedically oriented) family w...
Human Physiology: An Integrated Approach (8th Edition)
Determine the molecular geometry of each polyatomic ion. a. CO32 b. CIO2 c. NO3 d. NH4+
Introductory Chemistry (6th Edition)
1.14 Classify each of the following as a pure substance or a mixture. If a mixture, indicate whether it is homo...
Chemistry: The Central Science (14th Edition)
Use a globe or map to determine, as accurately as possible, the latitude and longitude of Athens, Greece.
Applications and Investigations in Earth Science (9th Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, physics and related others by exploring similar questions and additional content below.Similar questions
- 3.37(a) Five free electrons exist in a three-dimensional infinite potential well with all three widths equal to \( a = 12 \, \text{Å} \). Determine the Fermi energy level at \( T = 0 \, \text{K} \). (b) Repeat part (a) for 13 electrons. Book: Semiconductor Physics and Devices 4th ed, NeamanChapter-3Please expert answer only. don't give gpt-generated answers, & please clear the concept of quantum states for determining nx, ny, nz to determine E, as I don't have much idea about that topic.arrow_forward3.37(a) Five free electrons exist in a three-dimensional infinite potential well with all three widths equal to \( a = 12 \, \text{Å} \). Determine the Fermi energy level at \( T = 0 \, \text{K} \). (b) Repeat part (a) for 13 electrons. Book: Semiconductor Physics and Devices 4th ed, NeamanChapter-3Please expert answer only. don't give gpt-generated answers, & please clear the concept of quantum states for determining nx, ny, nz to determine E, as I don't have much idea about that topic.arrow_forwardNo chatgpt pls will upvotearrow_forward
- Use the following information to answer the next question. Two mirrors meet an angle, a, of 105°. A ray of light is incident upon mirror A at an angle, i, of 42°. The ray of light reflects off mirror B and then enters water, as shown below: Incident ray at A Note: This diagram is not to scale. a Air (n = 1.00) Water (n = 1.34) 1) Determine the angle of refraction of the ray of light in the water. Barrow_forwardHi can u please solvearrow_forward6. Bending a lens in OpticStudio or OSLO. In either package, create a BK7 singlet lens of 10 mm semi-diameter and with 10 mm thickness. Set the wavelength to the (default) 0.55 microns and a single on-axis field point at infinite object distance. Set the image distance to 200 mm. Make the first surface the stop insure that the lens is fully filled (that is, that the entrance beam has a radius of 10 mm). Use the lens-maker's equation to calculate initial glass curvatures assuming you want a symmetric, bi-convex lens with an effective focal length of 200 mm. Get this working and examine the RMS spot size using the "Text" tab of the Spot Diagram analysis tab (OpticStudio) or the Spd command of the text widnow (OSLO). You should find the lens is far from diffraction limited, with a spot size of more than 100 microns. Now let's optimize this lens. In OpticStudio, create a default merit function optimizing on spot size.Then insert one extra line at the top of the merit function. Assign the…arrow_forward
- No chatgpt pls will upvote Already got wrong chatgpt answer .arrow_forwardUse the following information to answer the next question. Two mirrors meet an angle, a, of 105°. A ray of light is incident upon mirror A at an angle, i, of 42°. The ray of light reflects off mirror B and then enters water, as shown below: A Incident ray at A Note: This diagram is not to scale. Air (n = 1.00) Water (n = 1.34) Barrow_forwardUse the following information to answer the next question. Two mirrors meet an angle, a, of 105°. A ray of light is incident upon mirror A at an angle, i, of 42°. The ray of light reflects off mirror B and then enters water, as shown below: A Incident ray at A Note: This diagram is not to scale. Air (n = 1.00) Water (n = 1.34) Barrow_forward
- Good explanation it sure experts solve it.arrow_forwardNo chatgpt pls will upvote Asaparrow_forwardA satellite has a mass of 100kg and is located at 2.00 x 10^6 m above the surface of the earth. a) What is the potential energy associated with the satellite at this loction? b) What is the magnitude of the gravitational force on the satellite?arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Classical Dynamics of Particles and SystemsPhysicsISBN:9780534408961Author:Stephen T. Thornton, Jerry B. MarionPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill
University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University
Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Classical Dynamics of Particles and Systems
Physics
ISBN:9780534408961
Author:Stephen T. Thornton, Jerry B. Marion
Publisher:Cengage Learning
Principles of Physics: A Calculus-Based Text
Physics
ISBN:9781133104261
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
Glencoe Physics: Principles and Problems, Student...
Physics
ISBN:9780078807213
Author:Paul W. Zitzewitz
Publisher:Glencoe/McGraw-Hill
University Physics Volume 1
Physics
ISBN:9781938168277
Author:William Moebs, Samuel J. Ling, Jeff Sanny
Publisher:OpenStax - Rice University
Physics for Scientists and Engineers, Technology ...
Physics
ISBN:9781305116399
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...
Physics
ISBN:9781133939146
Author:Katz, Debora M.
Publisher:Cengage Learning
Relative Velocity - Basic Introduction; Author: The Organic Chemistry Tutor;https://www.youtube.com/watch?v=_39hCnqbNXM;License: Standard YouTube License, CC-BY