Chapter 2, Problem 4CP

Jon Weideman, first shift foreman for Cut-Rate Machining, Inc., is attempting to decide on a vendor from whom to purchase a drilling machine. He narrows his alternatives to four vendors: The Hole-Maker, Inc. (HM); Shafts & Slips, Inc. (SS); Judge’s Jigs (JJ); and Drill-for-Bits, Inc. (DB). Each of these vendors is offering machines of similar capabilities at similar prices, so the effectiveness of the machines is the only selection criteria that Mr. Weideman can use. He invites each vendor to ship one machine to his Richmond, Indiana manufacturing facility for a test. He starts all four machines at 8:00 A.M. and lets them warm up for two hours before starting to use any of the machines. Sometime after the warmup period, one of his employees will use each of the shipped machines to drill 3-centimeter-diameter holes in 25-centimeter-thick stainless-steel sheets for two hours. The widths of holes drilled with each machine are then measured and recorded. The results of Mr. Weideman’s data collection are shown in Table 2.22.

TABLE 2.21 ANNUAL EXPENDITURES FOR QUEEN CITY (FIRST FOUR ENTRIES)

TABLE 2.22 DATA COLLECTED FOR DRILL-FOR-BITS, INC VENDOR SELECTION

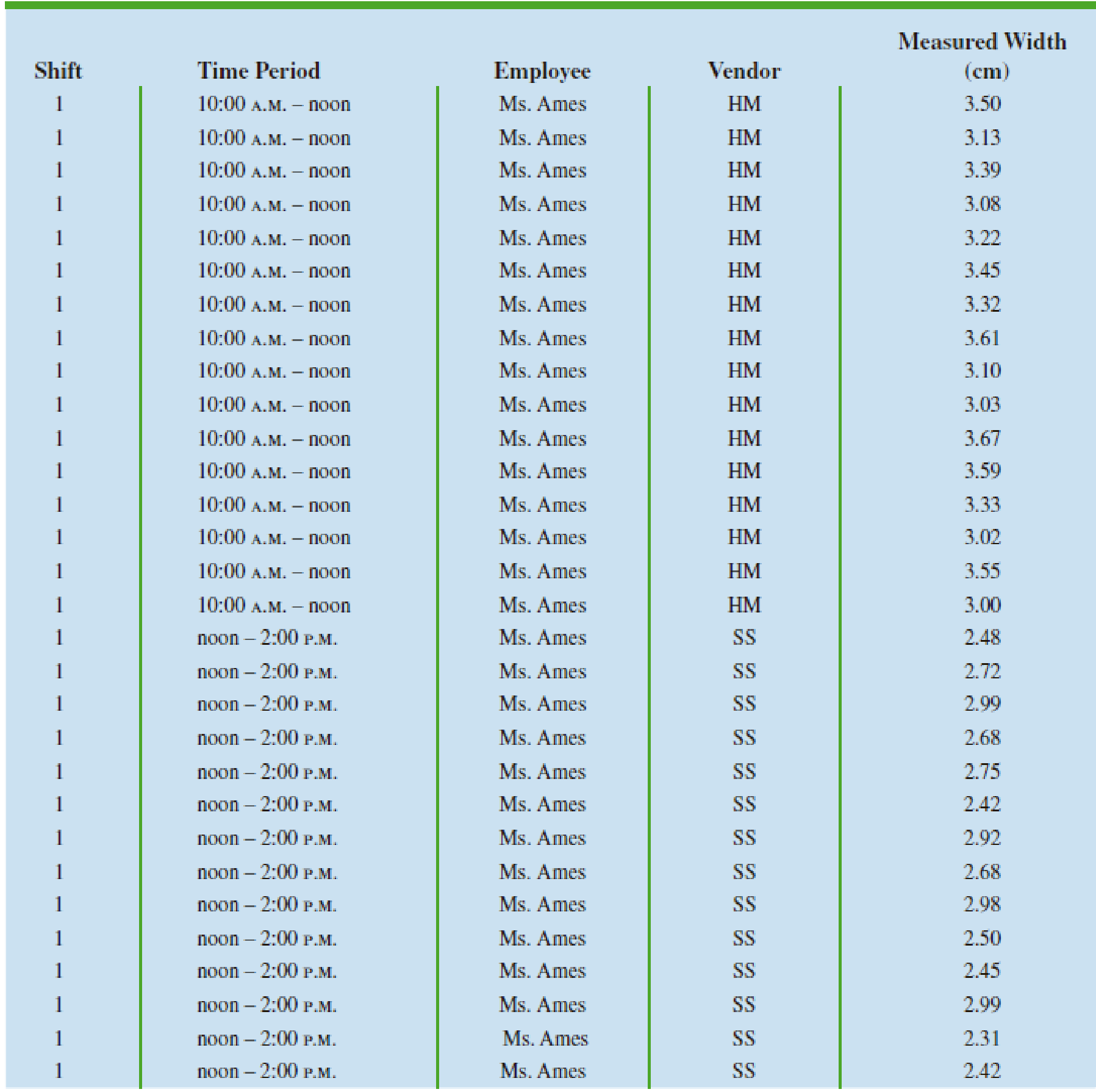
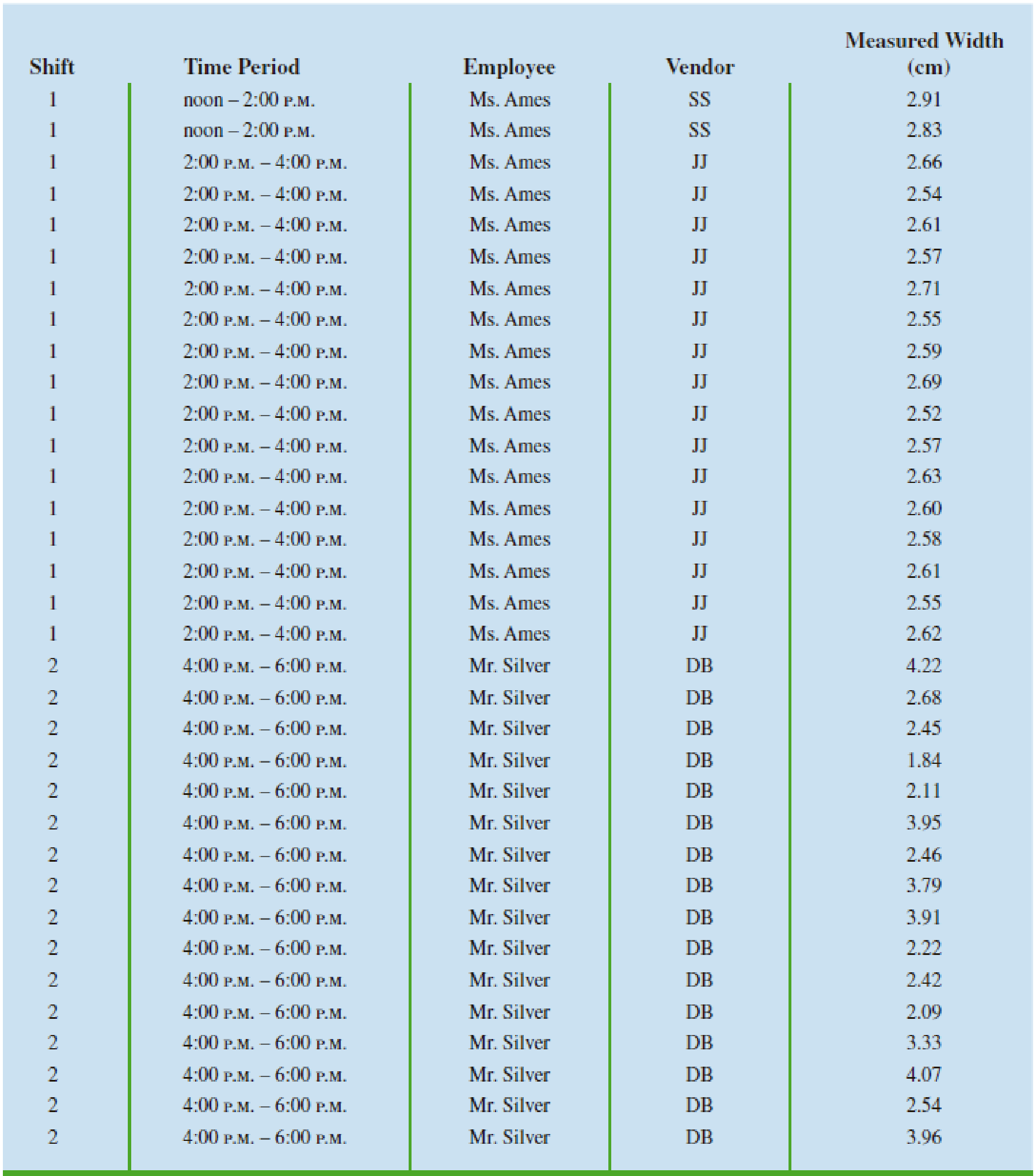
Based on these results, from which vendor would you suggest Mr. Weideman purchase his new machine?

Managerial Report

Use graphical methods of descriptive statistics to investigate the effectiveness of each vendor. Include the following in your report:

1. 1. Scatter plots of the measured width of each hole (cm).
2. 2. Based on the scatter plots, a discussion of the effectiveness of each vendor and under which conditions (if any) that vendor would be acceptable.
3. 3. A discussion of possible sources of error in the approach taken to assess these vendors.