Chapter 2, Problem 2.86P

To determine

The horizontal force (P) required to hold the gate.

Answer to Problem 2.86P

The force P = $58.7kN$

Explanation of Solution

Given information:

The quarter circle BC is hinged at point C.

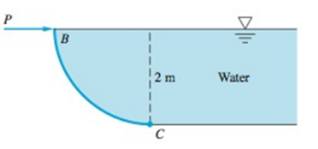The weight of the gate is neglected.

To find force P, the moment for the above system needs to be taken from point C. Therefore, the horizontal and the vertical water forces acting on the gate needs to be found with their respective point of action.

The width of the gate into the paper is not mentioned. Therefore, consider that as 3m.

Assume that the horizontal force acting on the panel is ${\text{F}}_{\text{H }}$ and can be given as below.

${\text{F}}_{\text{H }}=\gamma A{h}^1$

In above equation,

$\gamma$ - Specific weight of water and it’s equal to $9790N/m^2$

$A$ - Area which the horizontal force is acting on

$h^1$ - Distance between the top water level and the center of gravity of the panel (CG)

Assume that the vertical force acting on the panel is ${\text{F}}_{\text{v }}$ and can be given as below.

${\text{F}}_{\text{v }}=\gamma {(Vol)}_{above}BC$

$=\gamma Ah$

In above equation,

$\gamma$ - Specific weight of water and it’s equal to $9790N/m^2$

$A$ - Area above the panel

$h$ - Width of the panel

The below equation is used to find the line of action of horizontal force ${\text{F}}_{\text{H }}$

$y=-\frac{I}{A{h}^1}$

In above equation,

$y$ - Distance from the center of gravity (G) to the line of action.

$I$ - Inertia of the plane which the horizontal force is acting on.

$A$ - Area which the horizontal force is acting on

$h^1$ - Distance between the top water level and the center of gravity of the panel (CG)

Calculation:

To find horizontal force,

According to the above mentioned explanation,

$\begin{array}{l}{\text{F}}_{\text{H }}=\gamma A{h}^1\\ =9790N/m^2\left(2m\times 3m\right)\left(1m\right)\\ =58740N\end{array}$

Therefore, the horizontal component of the hydrostatic force = $58740N$

To find the line of action,

$y=-\frac{I}{A{h}^1}$

In this case, the inertia of the rectangular plane is equal to,

$I=\left(\frac{1}{12}b{h}^3\right)$

Therefore,

$\begin{array}{l}y=-\frac{I}{A{h}^1}\\ =-\frac{\left(\frac{1}{12}\times 3m\times {\left(2m\right)}^3\right)}{6m\times 1m}\\ =-0.333m\end{array}$

The horizontal force is acting at a distance $1+0.333=1.333m$ from point B, therefore distance from point C is equal to,

$2-1.333=0.667m$

To find vertical force,

According to the above mentioned explanation,

${\text{F}}_{\text{v }}=\gamma {(Vol)}_{above}BC$

$=\gamma Ah$

$\begin{array}{l}=\gamma h(AreaofABC)\\ =\left(9790N/m^2\right)\left(3m\right)\left(\frac{\pi 2^2}{4}\right)\\ =92268.57N\end{array}$

The vertical force acts at a distance equals to $\frac{4R}{3\pi }$ from left of point C.

Therefore,

$\begin{array}{l}\frac{4R}{3\pi }=\left(\frac{4\times 2m}{3\pi }\right)\\ =0.848m\end{array}$

The above values can be represented as below,

To find the magnitude of force P, take moment for the above system from point C in clockwise direction.

$\begin{array}{l}{\displaystyle \sum M_C=0}\\ 2P-(58740N\times 0.667m)-(92268.57\times 0.848m)=0\\ =58711.66N\\ \begin{array}{l}\hfill \end{array}=58.7kN\end{array}$ Conclusion:

The force P required to hold the gate stationary is equals to $58.7kN$.