
Concept explainers
The suspension of an automobile can be approximated by the simplified spring-and-dashpot system shown. (a) Write the differential equation defining the vertical displacement of the mass m when the system moves at a speed v over a road with a sinusoidal cross-section of amplitude δm and wavelength L. (b) Derive an expression for the amplitude of the vertical displacement of the mass m.
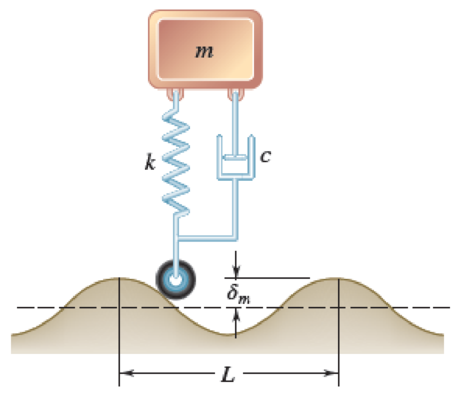
Fig. P19.151
(a)
Write the differential equation defining the vertical displacement of the mass m when the system moves at a speed v over a road with a sinusoidal cross section of amplitude
Answer to Problem 19.151P
The differential equation defining the vertical displacement of the mass m when the system moves at a speed v over a road with a sinusoidal cross section of amplitude
Explanation of Solution
Calculation:
Show the free body diagram of the system of automobile, spring and dashpot as in Figure (1).

The expression for the weight of the automobile (W) as follows:
Here,
The expression for the acceleration of the automobile (a) as follows:
Refer Figure (1),
The expression for the force by considering the vertical equilibrium condition as follows;
Substitute
Substitute
The expression for the time interval needed to travel
The expression for the forced circular frequency
Substitute
The expression for the motion of the wheel which is sine curve
Differentiate the above equation with respect to time ‘t’.
Substitute
Substitute
Therefore, the differential equation defining the vertical displacement of the mass m when the system moves at a speed v over a road with a sinusoidal cross section of amplitude
(b)
Derive an expression for the amplitude of the vertical displacement of the mass m.
Answer to Problem 19.151P
The expression for the amplitude of the vertical displacement of the mass m is
Explanation of Solution
Calculation:
The expression for the general solution from the identity as follows:
Here,
The expression for the force transmitted (F) to the automobile as follows:
Substitute
The expression for the differential equation of the motion for the damped forced vibration as follows:
Compare the equation (3) and (4).
The expression for the steady state of motion of the system as follows:
The expression for the steady state of motion of the system as follows:
Substitute
The expression for the phase angle
The expression for the Eulerian angle
Therefore, the expression for the amplitude of the vertical displacement of the mass m is
Want to see more full solutions like this?
Chapter 19 Solutions
VEC MECH 180-DAT EBOOK ACCESS(STAT+DYNA)
- A 4 ft 300 Ib 1000 Ib.ft 350 Ib C 2 ft 3. 45° 250 Ib B. 3ft B 25ft 200 Ib 150 Ib Replace the force system acting on the frame shown in the figure by a resultant force (magnitude and direction), and specify where its line of action intersects member (AB), measured from point (A).arrow_forwardCan you research the standard percentage of Steam Quality in:(1.) Boiler - leaving boilerBoiler -> Out(2.) Condenser - coming in condenser In -> CondenserProvide reference Also define: steam quality, its purpose and importancearrow_forwardNumbers 1 and 2 and 5 are are optional problems. However, I only need the values (with units) of 3, 4 and 6. Thank you :)arrow_forward
- Three cables are pulling on a ring located at the origin, as shown in the diagram below. FA is 200 N in magnitude with a transverse angle of 30° and an azimuth angle of 140°. FB is 240 N in magnitude with coordinate direction angles α = 135° and β = 45°. Determine the magnitude and direction of FC so that the resultant of all 3 force vectors lies on the z-axis and has a magnitude of 300 N. Specify the direction of FC using its coordinate direction angles.arrow_forwardturbomachieneryarrow_forwardauto controlsarrow_forward
- auto controlsarrow_forward1 Pleasearrow_forwardA spring cylinder system measures the pressure. Determine which spring can measure pressure between 0-1 MPa with a large excursion. The plate has a diameter of 20 mm. Also determine the displacement of each 0.1 MPa step.Spring power F=c x fF=Springpower(N)c=Spring constant (N/mm)f=Suspension (mm) How do I come up with right answer?arrow_forward
 Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY





