Chapter 19, Problem 19.165RP

A 4-lb uniform rod is supported by a pin at O and a spring at A and is connected to a dashpot at B. Determine (a) the differential equation of motion for small oscillations, (b) the angle that the rod will form with the horizontal 5 s after end B has been pushed 0.9 in. down and released.

Fig. P19.165

To determine

The differential equation of motion for small oscillations.

Answer to Problem 19.165RP

The differential equation of motion for small oscillations is $\underset{\_}{0.072464\ddot{\theta }+1.125\dot{\theta }+1.25\theta =0}$.

Explanation of Solution

Given information:

The weight of the uniform rod (W) is 4 lb.

The distance between A to O (a) is 6 inch.

The distance between O to B (b) is 18 in.

The spring constant (k) is 5 lb/ft.

The damping coefficient (c) is $\text{0}\text{.5}\text{lb}\cdot \text{s/ft}$.

The acceleration due to gravity (g) is $32.2\text{ft}/{\text{s}}^{\text{2}}$.

Calculation:

Calculate the mass of the uniform rod (m) using the formula:

$\begin{array}{c}W=mg\\ m=\frac{W}{g}\end{array}$

Substitute 4 lb for W and $32.2\text{ft}/{\text{s}}^{\text{2}}$ for g.

$\begin{array}{c}m=\frac{4}{32.2}\\ =0.124224\text{lb}\cdot {\text{s}}^{\text{2}}/\text{ft}\end{array}$

Show the free body diagram of the rod as Figure (1).

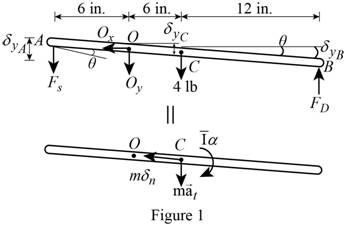
For small angle, take $\sin \theta$ as $\theta$ and $\cos \theta$ as 1.

Calculate the deflection at the point A $\left(\delta y_A\right)$ using the relation:

$\delta y_A=a\theta$

Substitute 6 in. for a.

$\begin{array}{c}\delta y_A=\left(\text{6in}\text{.×}\frac{\text{1}}{\text{12}}\frac{\text{ft}}{\text{in}\text{.}}\right)\theta \\ =\frac{\theta }{2}\end{array}$

Calculate the deflection at the point B $\left(\delta y_B\right)$ using the relation:

$\delta y_B=b\theta$

Substitute 18 in. for b.

$\begin{array}{c}\delta y_B=\left(\text{18in}\text{.×}\frac{\text{1}}{\text{12}}\frac{\text{ft}}{\text{in}\text{.}}\right)\theta \\ =\frac{3\theta }{2}\end{array}$

Calculate the deflection at the point C $\left(\delta y_C\right)$ using the relation:

$\delta y_C=a\theta$

Substitute 6 in. for a.

$\begin{array}{c}\delta y_C=\left(\text{6in}\text{.×}\frac{\text{1}}{\text{12}}\frac{\text{ft}}{\text{in}\text{.}}\right)\theta \\ =\frac{\theta }{2}\end{array}$

Take the moment about O.

$\begin{array}{l}{\displaystyle \sum M_O}={\left({\displaystyle \sum M_O}\right)}_{eff}\\ -\left[F_s\times \left(\frac{6}{12}\text{ft}\right)\right]+\left[4\times \left(\frac{6}{12}\text{ft}\right)\right]-\left[F_D\times \left(\frac{18}{12}\text{ft}\right)\right]=\overline{I}\alpha +\left[\left(m{\overline{a}}_t\right)\times \left(\frac{6}{12}\text{ft}\right)\right]\end{array}$ (1)

Calculate for the spring force $\left(F_s\right)$ using the relation:

$F_s=k\left(\delta y_A+{\left({\delta }_{st}\right)}_A\right)$

Substitute $\frac{\theta }{2}$ for $\delta y_A$.

$F_s=k\left(\frac{\theta }{2}+{\left({\delta }_{st}\right)}_A\right)$

Calculate the damping force $\left(F_D\right)$ using the relation:

$F_D=c\delta {\dot{y}}_B$

Substitute $\frac{3\dot{\theta }}{2}$ for $\delta {\dot{y}}_B$.

$F_D=c\frac{3\dot{\theta }}{2}$

Calculate the moment of inertia $\left(\overline{I}\right)$ of the rod using the formula:

$\overline{I}=\frac{1}{12}m{\left(a+b\right)}^2$

Substitute 6 in. for a and 18 in. for b.

$\begin{array}{c}\overline{I}=\frac{1}{12}m{\left(\frac{6+18}{12}\text{ft}\right)}^2\\ =\frac{1}{3}m\end{array}$

The angle $\left(\alpha \right)$ will be same as the angular acceleration $\left(\ddot{\theta }\right)$.

Calculate the acceleration $\left({\overline{a}}_t\right)$ using the relation:

${\overline{a}}_t=\left(a\right)\alpha$

Substitute 6 in. for a and $\ddot{\theta }$ for $\alpha$.

$\begin{array}{c}{\overline{a}}_t=\left(\frac{6}{12}\text{ft}\right)\ddot{\theta }\\ =\frac{\ddot{\theta }}{2}\end{array}$

Substitute $k\left(\frac{\theta }{2}+{\left({\delta }_{st}\right)}_A\right)$ for $F_s$, $c\frac{3\dot{\theta }}{2}$ for $F_D$, $\frac{1}{3}m$ for $\overline{I}$, $\ddot{\theta }$ for $\alpha$, and $\frac{\ddot{\theta }}{2}$ for ${\overline{a}}_t$ in Equation (1).

$\begin{array}{l}\left\{\begin{array}{l}-\left[k\left(\frac{\theta }{2}+{\left({\delta }_{st}\right)}_A\right)\times \left(\frac{6}{12}\text{ft}\right)\right]+\left[4\times \left(\frac{6}{12}\text{ft}\right)\right]\\ -\left[c\frac{3\dot{\theta }}{2}\times \left(\frac{18}{12}\text{ft}\right)\right]\end{array}\right\}=\left\{\begin{array}{l}\frac{1}{3}m\ddot{\theta }+\\ \left[\left(m\frac{\ddot{\theta }}{2}\right)\times \left(\frac{6}{12}\text{ft}\right)\right]\end{array}\right\}\\ \left\{\begin{array}{l}\frac{1}{3}m\ddot{\theta }+\left[\left(m\frac{\ddot{\theta }}{2}\right)\times \left(\frac{6}{12}\text{ft}\right)\right]+\left[k\left(\frac{\theta }{2}+{\left({\delta }_{st}\right)}_A\right)\times \left(\frac{6}{12}\text{ft}\right)\right]\\ -\left[4\times \left(\frac{6}{12}\text{ft}\right)\right]+\left[c\frac{3\dot{\theta }}{2}\times \left(\frac{18}{12}\text{ft}\right)\right]\end{array}\right\}=0\\ \frac{m}{3}\ddot{\theta }+\frac{m}{4}\ddot{\theta }+\frac{k}{2}\left(\frac{\theta }{2}+{\left({\delta }_{st}\right)}_A\right)-2+\frac{9}{4}c\dot{\theta }=0\end{array}$ (2)

Consider equilibrium.

Take the moment about O.

$\begin{array}{l}{\displaystyle \sum M_O}=0\\ k{\left({\delta }_{st}\right)}_A\left(\frac{6}{12}\text{ft}\right)-4\left(\frac{6}{12}\text{ft}\right)=0\\ \frac{k}{2}{\left({\delta }_{st}\right)}_A=4\left(\frac{6}{12}\text{ft}\right)\\ \frac{k}{2}{\left({\delta }_{st}\right)}_A=2\end{array}$

Substitute 2 for $\frac{k}{2}{\left({\delta }_{st}\right)}_A$ in Equation (2).

$\begin{array}{c}\frac{m}{3}\ddot{\theta }+\frac{m}{4}\ddot{\theta }+\left(\frac{k}{2}\frac{\theta }{2}+\frac{k}{2}{\left({\delta }_{st}\right)}_A\right)-2+\frac{9}{4}c\dot{\theta }=0\\ \frac{m}{3}\ddot{\theta }+\frac{m}{4}\ddot{\theta }+\frac{k}{2}\frac{\theta }{2}+2-2+\frac{9}{4}c\dot{\theta }=0\end{array}$

Substitute $0.124224\text{lb}\cdot {\text{s}}^{\text{2}}/\text{ft}$ for m, 5 lb/ft for k, and $\text{0}\text{.5}\text{lb}\cdot \text{s/ft}$ for c.

$\begin{array}{l}\frac{0.124224}{3}\ddot{\theta }+\frac{0.124224}{4}\ddot{\theta }+\frac{5}{2}\frac{\theta }{2}+2-2+\frac{9}{4}\left(0.5\right)\dot{\theta }=0\\ 0.041408\ddot{\theta }+0.031056\ddot{\theta }+2.5\left(0.5\theta \right)+1.125\dot{\theta }=0\\ 0.072464\ddot{\theta }+1.125\dot{\theta }+1.25\theta =0\end{array}$ (3)

Therefore, the differential equation of motion for small oscillations is $\underset{\_}{0.072464\ddot{\theta }+1.125\dot{\theta }+1.25\theta =0}$.

To determine

The angle that the rod $\left(\theta \right)$ will form with the horizontal 5 sec after end B has been pushed 0.9 in. down and released.

Answer to Problem 19.165RP

The angle that the rod $\left(\theta \right)$ is $\underset{\_}{0}$ and the rod return back to its equilibrium position after a finite time.

Explanation of Solution

Given information:

The weight of the uniform rod (W) is 4 lb.

The distance between A to O (a) is 6 inch.

The distance between O to B (b) is 18 inch.

The spring constant (k) is 5 lb/ft.

The damping coefficient (c) is $\text{0}\text{.5}\text{lb}\cdot \text{s/ft}$.

The acceleration due to gravity (g) is $32.2\text{ft}/{\text{s}}^{\text{2}}$.

Calculation:

Consider the equation (3).

Substitute $\lambda$ for $\theta$ in the equation (3).

$0.072464{\lambda }^2+1.125\lambda +1.25=0$

Solve the above equation.

$\begin{array}{l}{\lambda }_1=-1.2046\\ {\lambda }_2=-14.3204\end{array}$

Since the computed roots are real and distinct.

Write the expression for the general solution for the differential equation as follows:

$\theta =C_1{e}^{{\lambda }_{1}t}+C_2{e}^{{\lambda }_{2}t}$ (4)

Substitute 0 for t.

$\begin{array}{l}\theta \left(0\right)=C_1{e}^{{\lambda }_1\left(0\right)}+C_2{e}^{{\lambda }_2\left(0\right)}\\ 0=C_1+C_2\end{array}$

Differentiate the equation (4) with respect to time ‘t’.

$\dot{\theta }=C_{1}t{e}^{{\lambda }_{1}t}+C_{2}t{e}^{{\lambda }_{2}t}$

Substitute 0 for t.

$\begin{array}{c}\dot{\theta }\left(0\right)=C_1\left(0\right)e^{{\lambda }_1\left(0\right)}+C_2\left(0\right)e^{{\lambda }_2\left(0\right)}\\ =0\end{array}$

The above solution corresponds to a no vibratory motion because the roots ${\lambda }_1$ and ${\lambda }_2$ are both negative, then the values of the above solution will be zero as time ‘t’ increases indefinitely. Thus, the system returns back to its equilibrium position after a finite time.

Therefore, the angle that the rod $\left(\theta \right)$ is $\underset{\_}{0}$ and the rod return back to its equilibrium position after a finite time.