Vector Mechanics for Engineers: Dynamics
11th Edition
ISBN: 9780077687342
Author: Ferdinand P. Beer, E. Russell Johnston Jr., Phillip J. Cornwell, Brian Self
Publisher: McGraw-Hill Education
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 19.2, Problem 19.65P
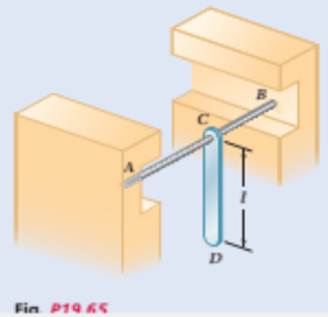
A 5-kg uniform rod CD of length
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
mechanical vibrations
question is image
Two identical circular cylinders of radius r and mass m each, are connected by a
spring, as shown below. Derive the equations of motion using Lagrange's equations. Please
indicate the lowest natural vibration frequency. (1 =mr?)
k
m
The 8-kg uniform bar AB is hinged at C and is attached at and A to a spring of constant==k = 500 N/m. If end A is given a small displacement and released, determine (a) the frequency of small oscillations, (b ) the smallest value of the spring constant k for which oscillations will occur.
Chapter 19 Solutions
Vector Mechanics for Engineers: Dynamics
Ch. 19.1 - A particle moves in simple harmonic motion....Ch. 19.1 - A particle moves in simple harmonic motion....Ch. 19.1 - Prob. 19.3PCh. 19.1 - Prob. 19.4PCh. 19.1 - Prob. 19.5PCh. 19.1 - Prob. 19.6PCh. 19.1 - A simple pendulum consisting of a bob attached to...Ch. 19.1 - A simple pendulum consisting of a bob attached to...Ch. 19.1 - A 10-Ib block A rests on a 40-Ib plate B that is...Ch. 19.1 - A 5-kg fragile glass vase is surrounded by packing...
Ch. 19.1 - Prob. 19.11PCh. 19.1 - Prob. 19.12PCh. 19.1 - Prob. 19.13PCh. 19.1 - Prob. 19.14PCh. 19.1 - Prob. 19.15PCh. 19.1 - Prob. 19.16PCh. 19.1 - Prob. 19.17PCh. 19.1 - Prob. 19.18PCh. 19.1 - Prob. 19.19PCh. 19.1 - Prob. 19.20PCh. 19.1 - A 50-kg block is supported by the spring...Ch. 19.1 - Prob. 19.22PCh. 19.1 - Two springs with constants k1and k2are connected...Ch. 19.1 - Prob. 19.24PCh. 19.1 - Prob. 19.25PCh. 19.1 - Prob. 19.26PCh. 19.1 - Prob. 19.27PCh. 19.1 - From mechanics of materials it is known that when...Ch. 19.1 - Prob. 19.29PCh. 19.1 - Prob. 19.30PCh. 19.1 - Prob. 19.31PCh. 19.1 - Prob. 19.32PCh. 19.1 - Prob. 19.33PCh. 19.1 - Prob. 19.34PCh. 19.1 - Using the data of Table 19.1, determine the period...Ch. 19.1 - Prob. 19.36PCh. 19.2 - The uniform rod shown has mass 6 kg and is...Ch. 19.2 - Prob. 19.38PCh. 19.2 - A 6-kg uniform cylinder can roll without sliding...Ch. 19.2 - A 6-kg uniform cylinder is assumed to roll without...Ch. 19.2 - Prob. 19.41PCh. 19.2 - Prob. 19.42PCh. 19.2 - A square plate of mass m is held by eight springs,...Ch. 19.2 - Prob. 19.44PCh. 19.2 - Prob. 19.45PCh. 19.2 - Prob. 19.46PCh. 19.2 - Prob. 19.47PCh. 19.2 - Prob. 19.48PCh. 19.2 - Prob. 19.49PCh. 19.2 - Prob. 19.50PCh. 19.2 - A thin homogeneous wire is bent into the shape of...Ch. 19.2 - A compound pendulum is defined as a rigid body...Ch. 19.2 - Prob. 19.53PCh. 19.2 - Prob. 19.54PCh. 19.2 - Prob. 19.55PCh. 19.2 - Two uniform rods each have a mass m and length I...Ch. 19.2 - Prob. 19.57PCh. 19.2 - A 1300-kg sports car has a center of gravity G...Ch. 19.2 - A 6-lb slender rod is suspended from a steel wire...Ch. 19.2 - A uniform disk of radius r=250 mm is attached at A...Ch. 19.2 - Prob. 19.61PCh. 19.2 - Prob. 19.62PCh. 19.2 - Prob. 19.63PCh. 19.2 - Prob. 19.64PCh. 19.2 - A 5-kg uniform rod CD of length l=0.7 m is welded...Ch. 19.2 - A uniform equilateral triangular plate with a side...Ch. 19.2 - Prob. 19.67PCh. 19.2 - Prob. 19.68PCh. 19.3 - Prob. 19.69PCh. 19.3 - Prob. 19.70PCh. 19.3 - Prob. 19.71PCh. 19.3 - Prob. 19.72PCh. 19.3 - Prob. 19.73PCh. 19.3 - Prob. 19.74PCh. 19.3 - Prob. 19.75PCh. 19.3 - A homogeneous wire of length 2l is bent as shown...Ch. 19.3 - A uniform disk of radius r and mass m can roll...Ch. 19.3 - Prob. 19.78PCh. 19.3 - Prob. 19.79PCh. 19.3 - Prob. 19.80PCh. 19.3 - A slender 10-kg bar AB with a length of l=0.6 m is...Ch. 19.3 - Prob. 19.82PCh. 19.3 - Prob. 19.83PCh. 19.3 - Prob. 19.84PCh. 19.3 - Prob. 19.85PCh. 19.3 - Prob. 19.86PCh. 19.3 - Prob. 19.87PCh. 19.3 - Prob. 19.88PCh. 19.3 - Prob. 19.89PCh. 19.3 - Prob. 19.90PCh. 19.3 - Prob. 19.91PCh. 19.3 - Prob. 19.92PCh. 19.3 - The motion of the uniform rod AB is guided by the...Ch. 19.3 - Prob. 19.94PCh. 19.3 - Prob. 19.95PCh. 19.3 - Prob. 19.96PCh. 19.3 - Prob. 19.97PCh. 19.3 - Prob. 19.98PCh. 19.4 - Prob. 19.99PCh. 19.4 - Prob. 19.100PCh. 19.4 - Prob. 19.101PCh. 19.4 - Prob. 19.102PCh. 19.4 - Prob. 19.103PCh. 19.4 - Prob. 19.104PCh. 19.4 - Prob. 19.105PCh. 19.4 - Prob. 19.106PCh. 19.4 - Prob. 19.107PCh. 19.4 - The crude-oil pumping rig shown is driven at 20...Ch. 19.4 - Prob. 19.109PCh. 19.4 - Prob. 19.110PCh. 19.4 - Prob. 19.111PCh. 19.4 - Prob. 19.112PCh. 19.4 - Prob. 19.113PCh. 19.4 - Prob. 19.114PCh. 19.4 - Prob. 19.115PCh. 19.4 - Prob. 19.116PCh. 19.4 - Prob. 19.117PCh. 19.4 - Prob. 19.118PCh. 19.4 - Prob. 19.119PCh. 19.4 - Prob. 19.120PCh. 19.4 - Prob. 19.121PCh. 19.4 - Prob. 19.122PCh. 19.4 - Prob. 19.123PCh. 19.4 - Prob. 19.124PCh. 19.4 - Prob. 19.125PCh. 19.4 - A small trailer and its load have a total mass of...Ch. 19.5 - Prob. 19.127PCh. 19.5 - Prob. 19.128PCh. 19.5 - Prob. 19.129PCh. 19.5 - Prob. 19.130PCh. 19.5 - Prob. 19.131PCh. 19.5 - Prob. 19.132PCh. 19.5 - Prob. 19.133PCh. 19.5 - Prob. 19.134PCh. 19.5 - Prob. 19.135PCh. 19.5 - Prob. 19.136PCh. 19.5 - Prob. 19.137PCh. 19.5 - A 0.9-kg block B is connected by a cord to a...Ch. 19.5 - Prob. 19.139PCh. 19.5 - Prob. 19.140PCh. 19.5 - Prob. 19.141PCh. 19.5 - Prob. 19.142PCh. 19.5 - Prob. 19.143PCh. 19.5 - Prob. 19.144PCh. 19.5 - Prob. 19.145PCh. 19.5 - Prob. 19.146PCh. 19.5 - Prob. 19.147PCh. 19.5 - Prob. 19.148PCh. 19.5 - A simplified model of a washing machine is shown....Ch. 19.5 - Prob. 19.150PCh. 19.5 - Prob. 19.151PCh. 19.5 - Prob. 19.152PCh. 19.5 - Prob. 19.153PCh. 19.5 - Prob. 19.154PCh. 19.5 - Prob. 19.155PCh. 19.5 - Prob. 19.156PCh. 19.5 - Write the differential equations defining (a) the...Ch. 19.5 - Write the differential equations defining (a) the...Ch. 19 - Prob. 19.159RPCh. 19 - Prob. 19.160RPCh. 19 - Prob. 19.161RPCh. 19 - Prob. 19.162RPCh. 19 - Prob. 19.163RPCh. 19 - Prob. 19.164RPCh. 19 - A 4-lb uniform rod is supported by a pin at O and...Ch. 19 - Prob. 19.166RPCh. 19 - Prob. 19.167RPCh. 19 - Prob. 19.168RPCh. 19 - Prob. 19.169RPCh. 19 - Prob. 19.170RP
Additional Engineering Textbook Solutions
Find more solutions based on key concepts
What is the weight in newtons of an object that has a mass of (a) 8 kg, (b) 0.04 kg, (c) 760 Mg?
Statics and Mechanics of Materials (5th Edition)
Assume the following vectors are already defined: V1=[302]V2=[214]V3=[5131]V4=[0.50.10.20.2] For each of the fo...
Thinking Like an Engineer: An Active Learning Approach (4th Edition)
What parts are included in the vehicle chassis?
Automotive Technology: Principles, Diagnosis, And Service (6th Edition) (halderman Automotive Series)
The triple jump is a track-and-field event in which an athlete gets a running start and tries to leap as far as...
Vector Mechanics For Engineers
Locate the centroid of the area. Prob. 9-17
INTERNATIONAL EDITION---Engineering Mechanics: Statics, 14th edition (SI unit)
A biological fluid moves at a flow rate of m=0.02kg/s through a coiled, thin-walled, 5-mm-diameter tube submerg...
Fundamentals of Heat and Mass Transfer
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, mechanical-engineering and related others by exploring similar questions and additional content below.Similar questions
- A body weighing 5kg is attached to a very light bar as depicted below. The set-up is free to rotate in the vertical plane about pin support O. The force applied at point C makes the bar oscillate(via small rotation) about the position of equilibrium illustrated below Compute the amplitude θ and the phase angle Φarrow_forward2) A massless bar of length L carrying a tip mass m is rigidly connected to a homogenous disk of radius R and mass m as shown below. The disk rolls without slipping on the ground. Note that gravity acts down and that a spring of stiffness k and a dashpot of constant c connect the center of the disk to an oscillating wall and a fixed one respectively. Determine the amplitude of response of the angle 0(t).arrow_forward2. The weightless rod carries two masses m. one at a distance L from the pivot or the other at 2L. If the rod is rotated by a small angle e and released, determine the following: a. the differential equation of motion of the system, and b. the natural frequency of vibration of the rod. (J. - mc?, where c dist amce from mass m to pivot 0.)arrow_forward
- The homogeneous rod OA is supported at point 0, and a mass of 2m is attached at the bottom of the system as shown. For small oscillations and by use of ENERGY METHOD;arrow_forwardA 4-lb uniform rod is supported by a pin at O and a spring at A and is connected to a dashpot at B. Determine (a) the differential equation of motion for small oscillations, (b ) the angle that the rod will form with the horizontal 5 s after end B has been pushed 0.9 in. down and released.arrow_forwardWant in detailarrow_forward
- Two identical spring-mass systems A and B are coupled by a weak middle spring having a spring constant smaller by a factor of 100 (i.e. 100kmiddle = kA = kB). Mass A is pulled by a small distance and released from rest, while mass B is released from rest at its equilibrium position, at t = 0. Calculate the approximate number of oscillations completed by mass A before its oscillations die down first.arrow_forward2. A point mass m is strung on a vertical ring of radius R, and it oscillates freely with respect to its equilibrium point located at the lowest point of the ring. An external moment of force is applied that causes the ring to oscillate about its center in the form α = α₁ cost where a is the angle of rotation. Determine the general movement of the mass m, and under what circumstances this movement enters into resonance, detailing this phenomenon.arrow_forwardQ.1 The system shown below consists of a block of mass m and a cylinder of mass 2m. The block and the cylinder are joined by pulley arrangement as show. The coordinates x and y are dependent in which x = 2y. Use m= 2 kg. The angle 0 is any value between 0 and 90°. If the cylinder is pushed downward 20 mm and released a) find the subsequent response of the block, x(1) b) find the displacement and velocity of the block at t = 1 s. The specific value of k is given in separate excel sheet. K=1985 2m IT, x = 2yarrow_forward
- A thin cylindrical rod of uniform mass m and length L is suspended from the ends by two massless springs with constants k1 and k2 (Distance L1 and L2 on either side of the center of mass of the rod). The motion of the center of mass is constrained to move up and down parallel to the vertical y-axis. It also experiences rotational oscillations around an axis perpendicular to the rod and passing through the center of mass (I is the moment of inertia with respect to said axis). be y1 and y2 the displacements of the two ends from their equilibrium positions, as shown in Fig. a) Find the motion's equation (consider k1=k2=k)arrow_forwardY2arrow_forwardsolve this without the application of MOMENTS please. the answer is attached alsoarrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Elements Of Electromagnetics
Mechanical Engineering
ISBN:9780190698614
Author:Sadiku, Matthew N. O.
Publisher:Oxford University Press
Mechanics of Materials (10th Edition)
Mechanical Engineering
ISBN:9780134319650
Author:Russell C. Hibbeler
Publisher:PEARSON
Thermodynamics: An Engineering Approach
Mechanical Engineering
ISBN:9781259822674
Author:Yunus A. Cengel Dr., Michael A. Boles
Publisher:McGraw-Hill Education
Control Systems Engineering
Mechanical Engineering
ISBN:9781118170519
Author:Norman S. Nise
Publisher:WILEY
Mechanics of Materials (MindTap Course List)
Mechanical Engineering
ISBN:9781337093347
Author:Barry J. Goodno, James M. Gere
Publisher:Cengage Learning
Engineering Mechanics: Statics
Mechanical Engineering
ISBN:9781118807330
Author:James L. Meriam, L. G. Kraige, J. N. Bolton
Publisher:WILEY
Mechanical SPRING DESIGN Strategy and Restrictions in Under 15 Minutes!; Author: Less Boring Lectures;https://www.youtube.com/watch?v=dsWQrzfQt3s;License: Standard Youtube License