
Concept explainers
To graph: The
Explanation of Solution
Given information:
The quadratic equation
Graph:
The graph of the quadratic equation
Consider the quadratic equation,
Now put the values of
Solve the equation
The quadratic formula is:
Now solve the equation
Find the value of
The value of
Thus, the value of:
Substitute the values of
The quadratic formula is:
Either the value
When the value
When the value
So
Here observed the equation of parabola, the coefficient of
The roots and the shape of parabola is cleared.
The graph of the equation
Substitute
Substitute
Substitute
Observe that as the value of
Steps to plot the graph of the equation
Step 1: Press
Step 2: Use the down arrow key to reach
Step 3: Press
Step 4: Press
Step 5: Enter the function
Step 6: Press
For better view of graph.
Step 8: Press
The result obtained on the screen is provided below,
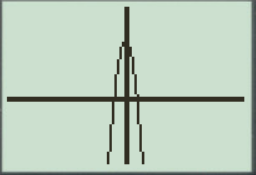
Interpretation:
The equation of the function
The parabola opens downward.
The
Therefore, in the equation,
Therefore, the equation
a.
When the
Steps to plot the graph of the equation
Step 1: Press
Step 2: Use the down arrow key to reach
Step 3: Press
Step 4: Press
Step 5: Enter the function
Step 6: Press
For better view of graph.
Step 8: Press
The result obtained on the screen is provided below,
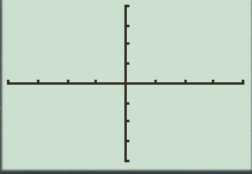
This window is not perfect viewing window.
b.
When the
Steps to plot the graph of the equation
Step 1: Press
Step 2: Use the down arrow key to reach
Step 3: Press
Step 4: Press
Step 5: Enter the function
Step 6: Press
For better view of graph.
Step 8: Press
The result obtained on the screen is provided below,

This window is not a perfect viewing window.
c.
When the
Steps to plot the graph of the equation
Step 1: Press
Step 2: Use the down arrow key to reach
Step 3: Press
Step 4: Press
Step 5: Enter the function
Step 6: Press
For better view of graph.
Step 8: Press
The result obtained on the screen is provided below,

This is the perfect viewing window.
d.
When the
Steps to plot the graph of the equation
Step 1: Press
Step 2: Use the down arrow key to reach
Step 3: Press
Step 4: Press
Step 5: Enter the function
Step 6: Press
For better view of graph.
Step 8: Press
The result obtained on the screen is provided below,
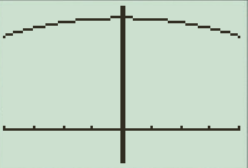
This window has large view, in this the graph points are not clear.
So perfect viewing window of the graph
Thus, option ‘c’
Chapter 1 Solutions
Precalculus: Mathematics for Calculus - 6th Edition
- Evaluate the triple integral 3' 23 HIG 2 +3 f(x, y, z)dxdydz where f(x, y, z) = x + 2x-y ม u = v = and w = 2 2 3 Triple Integral Region R -2 x N 2 y 3arrow_forwardFind the volume of the solid bounded below by the circular cone z = 2.5√√√x² + y² and above by the sphere x² + y²+z² = 6.5z.arrow_forwardElectric charge is distributed over the triangular region D shown below so that the charge density at (x, y) is σ(x, y) = 4xy, measured in coulumbs per square meter (C/m²). Find the total charge on D. Round your answer to four decimal places. 1 U 5 4 3 2 1 1 2 5 7 coulumbsarrow_forward
- Let E be the region bounded cone z = √√/6 - (x² + y²) and the sphere z = x² + y² + z² . Provide an answer accurate to at least 4 significant digits. Find the volume of E. Triple Integral Spherical Coordinates Cutout of sphere is for visual purposes 0.8- 0.6 z 04 0.2- 0- -0.4 -0.2 04 0 0.2 0.2 x -0.2 04 -0.4 Note: The graph is an example. The scale and equation parameters may not be the same for your particular problem. Round your answer to 4 decimal places. Hint: Solve the cone equation for phi. * Oops - try again.arrow_forwardThe temperature at a point (x,y,z) of a solid E bounded by the coordinate planes and the plane 9.x+y+z = 1 is T(x, y, z) = (xy + 8z +20) degrees Celcius. Find the average temperature over the solid. (Answer to 4 decimal places). Average Value of a function using 3 variables z 1- y Hint: y = -a·x+1 * Oops - try again. xarrow_forwardFind the saddle pointsarrow_forward
- For the curve defined by r(t) = (e** cos(t), et sin(t)) find the unit tangent vector, unit normal vector, normal acceleration, and tangential acceleration at t = πT 3 T (1) N Ň (1) 133 | aN = 53 ar = = =arrow_forwardFind the tangential and normal components of the acceleration vector for the curve - F(t) = (2t, −3t³, −3+¹) at the point t = 1 - ā(1) = T + Ñ Give your answers to two decimal placesarrow_forwardFind the unit tangent vector to the curve defined by (t)=(-2t,-4t, √√49 - t²) at t = −6. T(−6) =arrow_forward
- An airplane flies due west at an airspeed of 428 mph. The wind blows in the direction of 41° south of west at 50 mph. What is the ground speed of the airplane? What is the bearing of the airplane? 428 mph 41° 50 mph a. The ground speed of the airplane is b. The bearing of the airplane is mph. south of west.arrow_forwardRylee's car is stuck in the mud. Roman and Shanice come along in a truck to help pull her out. They attach one end of a tow strap to the front of the car and the other end to the truck's trailer hitch, and the truck starts to pull. Meanwhile, Roman and Shanice get behind the car and push. The truck generates a horizontal force of 377 lb on the car. Roman and Shanice are pushing at a slight upward angle and generate a force of 119 lb on the car. These forces can be represented by vectors, as shown in the figure below. The angle between these vectors is 20.2°. Find the resultant force (the vector sum), then give its magnitude and its direction angle from the positive x-axis. 119 lb 20.2° 377 lb a. The resultant force is (Tip: omit degree notations from your answers; e.g. enter cos(45) instead of cos(45°)) b. It's magnitude is lb. c. It's angle from the positive x-axis isarrow_forwardFind a plane containing the point (3, -3, 1) and the line of intersection of the planes 2x + 3y - 3z = 14 and -3x - y + z = −21. The equation of the plane is:arrow_forward
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





