VECTOR MECH. FOR EGR: STATS & DYNAM (LL
12th Edition
ISBN: 9781260663778
Author: BEER
Publisher: MCG
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 19, Problem 19.162RP
A small trailer and its load have a total mass of 250 kg. The trailer is supported by two springs, and when the boat is given an initial displacement x0 downward and released from rest, the amplitude of oscillation is reduced to ¼ x0 after one half cycle and the period of the oscillation is 0.8 s. The trailer is then pulled over a road, the surface of which can be approximated by a sine curve with an amplitude of 35 mm and a wavelength of 5 m (i.e., the distance between successive crests is 5 m and the vertical distance from crest to trough is 70 mm). Determine (a) the damping ratio, (b) the spring stiffness, (c) the amplitude of the vibration of the trailer at a speed of 50 km/h. (Hint: Use the logarithmic decrement discussed in Probs. 19.129 and 19.130.)
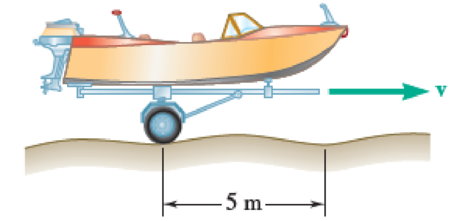
Fig. P19.162
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
A glider of mass 0.350 kg is placed on a frictionless, horizontal air track. One end of a horizontal spring is attached to the glider, and the other end is attached to the end of the track. When released, the glider oscillates in SHM with frequency 4.15 Hz. Find the period of the motion.
Find the angular frequency of the motion. Find the force constant kk of the spring.
Find the magnitude of the force that the spring exerts on the glider when the spring is stretched by 0.0200 m.
An object of mass 2 kg is attached to a spring of stiffness 200 N / m on a horizontal frictionless surface . Then it is extend by 10 cm and then let free to oscillate . 1- How long will it take to make one complete oscillation ? 2- Determine the amplitude and give an expression for the displacement as a function of time . 3- Calculate its displacement , velocity , acceleration and force acting on it after sec . 4- Calculate its velocity by the time it is extended by 0.5 cm
Please
Chapter 19 Solutions
VECTOR MECH. FOR EGR: STATS & DYNAM (LL
Ch. 19.1 - A particle moves in simple harmonic motion....Ch. 19.1 - A particle moves in simple harmonic motion....Ch. 19.1 - Prob. 19.3PCh. 19.1 - Prob. 19.4PCh. 19.1 - Prob. 19.5PCh. 19.1 - Prob. 19.6PCh. 19.1 - Prob. 19.7PCh. 19.1 - A simple pendulum consisting of a bob attached to...Ch. 19.1 - Prob. 19.9PCh. 19.1 - Prob. 19.10P
Ch. 19.1 - Prob. 19.11PCh. 19.1 - Prob. 19.12PCh. 19.1 - Prob. 19.13PCh. 19.1 - Prob. 19.14PCh. 19.1 - A 5-kg collar C is released from rest in the...Ch. 19.1 - Prob. 19.16PCh. 19.1 - Prob. 19.17PCh. 19.1 - An 11-lb block is attached to the lower end of a...Ch. 19.1 - Block A has a mass m and is supported by the...Ch. 19.1 - A 13.6-kg block is supported by the spring...Ch. 19.1 - Prob. 19.21PCh. 19.1 - 19.21 and 19.22A 50-kg block is supported by the...Ch. 19.1 - Prob. 19.23PCh. 19.1 - The period of vibration of the system shown is...Ch. 19.1 - Prob. 19.25PCh. 19.1 - Prob. 19.26PCh. 19.1 - From mechanics of materials, it is known that for...Ch. 19.1 - From mechanics of materials it is known that when...Ch. 19.1 - Prob. 19.29PCh. 19.1 - Prob. 19.30PCh. 19.1 - If h = 700 mm and d = 500 mm and each spring has a...Ch. 19.1 - Prob. 19.32PCh. 19.1 - Prob. 19.33PCh. 19.1 - Prob. 19.34PCh. 19.1 - Prob. 19.35PCh. 19.1 - Prob. 19.36PCh. 19.2 - The 9-kg uniform rod AB is attached to springs at...Ch. 19.2 - Prob. 19.38PCh. 19.2 - Prob. 19.39PCh. 19.2 - Prob. 19.40PCh. 19.2 - A 15-lb slender rod AB is riveted to a 12-lb...Ch. 19.2 - A 20-lb uniform cylinder can roll without sliding...Ch. 19.2 - A square plate of mass m is held by eight springs,...Ch. 19.2 - Prob. 19.44PCh. 19.2 - Prob. 19.45PCh. 19.2 - A three-blade wind turbine used for research is...Ch. 19.2 - A connecting rod is supported by a knife-edge at...Ch. 19.2 - A semicircular hole is cut in a uniform square...Ch. 19.2 - A uniform disk of radius r = 250 mm is attached at...Ch. 19.2 - A small collar of mass 1 kg is rigidly attached to...Ch. 19.2 - Prob. 19.51PCh. 19.2 - Prob. 19.52PCh. 19.2 - Prob. 19.53PCh. 19.2 - Prob. 19.54PCh. 19.2 - The 8-kg uniform bar AB is hinged at C and is...Ch. 19.2 - Prob. 19.56PCh. 19.2 - Prob. 19.57PCh. 19.2 - Prob. 19.58PCh. 19.2 - Prob. 19.59PCh. 19.2 - Prob. 19.60PCh. 19.2 - Two uniform rods, each of weight W = 24 lb and...Ch. 19.2 - A homogeneous rod of mass per unit length equal to...Ch. 19.2 - Prob. 19.63PCh. 19.2 - Prob. 19.64PCh. 19.2 - A 60-kg uniform circular plate is welded to two...Ch. 19.2 - Prob. 19.66PCh. 19.2 - Prob. 19.67PCh. 19.2 - The centroidal radius of gyration ky of an...Ch. 19.3 - Two blocks each have a mass 1.5 kg and are...Ch. 19.3 - Prob. 19.70PCh. 19.3 - Prob. 19.71PCh. 19.3 - Prob. 19.72PCh. 19.3 - Prob. 19.73PCh. 19.3 - Prob. 19.74PCh. 19.3 - Prob. 19.75PCh. 19.3 - Prob. 19.76PCh. 19.3 - Prob. 19.77PCh. 19.3 - Blade AB of the experimental wind-turbine...Ch. 19.3 - A 15-lb uniform cylinder can roll without sliding...Ch. 19.3 - Prob. 19.80PCh. 19.3 - Prob. 19.81PCh. 19.3 - Prob. 19.82PCh. 19.3 - Prob. 19.83PCh. 19.3 - Prob. 19.84PCh. 19.3 - A homogeneous rod of weight W and length 2l is...Ch. 19.3 - A 10-lb uniform rod CD is welded at C to a shaft...Ch. 19.3 - Prob. 19.87PCh. 19.3 - Prob. 19.88PCh. 19.3 - Prob. 19.89PCh. 19.3 - Prob. 19.90PCh. 19.3 - Prob. 19.91PCh. 19.3 - Prob. 19.92PCh. 19.3 - Prob. 19.93PCh. 19.3 - A uniform rod of length L is supported by a...Ch. 19.3 - Prob. 19.95PCh. 19.3 - Three collars each have a mass m and are connected...Ch. 19.3 - Prob. 19.97PCh. 19.3 - As a submerged body moves through a fluid, the...Ch. 19.4 - A 4-kg collar can slide on a frictionless...Ch. 19.4 - Prob. 19.100PCh. 19.4 - A collar with mass m that slides on a frictionless...Ch. 19.4 - Prob. 19.102PCh. 19.4 - The 1.2-kg bob of a simple pendulum of length l =...Ch. 19.4 - Prob. 19.104PCh. 19.4 - A precision experiment sits on an optical table...Ch. 19.4 - Prob. 19.106PCh. 19.4 - Prob. 19.107PCh. 19.4 - The crude-oil pumping rig shown is driven at 20...Ch. 19.4 - Prob. 19.109PCh. 19.4 - Prob. 19.110PCh. 19.4 - Prob. 19.111PCh. 19.4 - Rod AB is rigidly attached to the frame of a motor...Ch. 19.4 - Prob. 19.113PCh. 19.4 - Prob. 19.114PCh. 19.4 - A motor of weight 100 lb is supported by four...Ch. 19.4 - Prob. 19.116PCh. 19.4 - Prob. 19.117PCh. 19.4 - Prob. 19.118PCh. 19.4 - Prob. 19.119PCh. 19.4 - One of the tail rotor blades of a helicopter has...Ch. 19.4 - Prob. 19.121PCh. 19.4 - Prob. 19.122PCh. 19.4 - Prob. 19.123PCh. 19.4 - Prob. 19.124PCh. 19.4 - A 60-lb disk is attached with an eccentricity e =...Ch. 19.4 - A small trailer and its load have a total mass of...Ch. 19.5 - Prob. 19.127PCh. 19.5 - Prob. 19.128PCh. 19.5 - Prob. 19.129PCh. 19.5 - Prob. 19.130PCh. 19.5 - Prob. 19.131PCh. 19.5 - Prob. 19.132PCh. 19.5 - Prob. 19.133PCh. 19.5 - Prob. 19.134PCh. 19.5 - Prob. 19.135PCh. 19.5 - Prob. 19.136PCh. 19.5 - Prob. 19.137PCh. 19.5 - Prob. 19.138PCh. 19.5 - A machine element weighing 500 lb is supported by...Ch. 19.5 - Prob. 19.140PCh. 19.5 - Prob. 19.141PCh. 19.5 - Prob. 19.142PCh. 19.5 - Prob. 19.143PCh. 19.5 - A 36-lb motor is bolted to a light horizontal beam...Ch. 19.5 - One of the tail rotor blades of a helicopter has...Ch. 19.5 - Prob. 19.146PCh. 19.5 - Prob. 19.147PCh. 19.5 - Prob. 19.148PCh. 19.5 - Prob. 19.149PCh. 19.5 - Prob. 19.150PCh. 19.5 - The suspension of an automobile can be...Ch. 19.5 - Prob. 19.152PCh. 19.5 - Prob. 19.153PCh. 19.5 - Prob. 19.154PCh. 19.5 - 19.155 and 19.156 Draw the electrical analog of...Ch. 19.5 - Prob. 19.156PCh. 19.5 - 19.157 and 19.158Write the differential equations...Ch. 19.5 - 19.157 and 19.158Write the differential equations...Ch. 19 - An automobile wheel-and-tire assembly of total...Ch. 19 - Prob. 19.160RPCh. 19 - Disks A and B weigh 30 lb and 12 lb, respectively,...Ch. 19 - A small trailer and its load have a total mass of...Ch. 19 - A 0.8-lb ball is connected to a paddle by means of...Ch. 19 - Prob. 19.164RPCh. 19 - A 4-lb uniform rod is supported by a pin at O and...Ch. 19 - Prob. 19.166RPCh. 19 - Prob. 19.167RPCh. 19 - A small ball of mass m attached at the midpoint of...Ch. 19 - Prob. 19.169RPCh. 19 - If either a simple or a compound pendulum is used...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, mechanical-engineering and related others by exploring similar questions and additional content below.Similar questions
- 3. A spring with spring constant 20N/m is attached to a 5kg mass with negligible friction. Determine the period, natural frequency, amplitude, and phase angle that the spring mass system will oscillate at initial displacement and velocity of 0.2m and zero respectively. A = Wn = T =arrow_forwardT1= 0.62 s T2= 0.54 s K1= 2440 n/marrow_forwardAn undamped 2.11 kg horizontal spring oscillator has a spring constant of 21.9 N/m. While oscillating, it is found to have a speed of 2.49 m/s as it passes through its equilibrium position. What is its amplitude A of oscillation? A = What is the oscillator's total mechanical energy Eot as it passes through a position that is 0.649 of the amplitude away from the equilibrium position? Etot = about us careers privacy policy terms of use contact us helparrow_forward
- Solve the problem. A particle is attached to a spring that creates a vibration with a frequency of 8 Hz. Determine the period of vibrations and the angular frequency.arrow_forwardAn automobile whose weight is 150 N and it is mounted on 4 identical springs due to its weight it sags by 250 mm . each shock absorber has damping coefficient of 0.4 N for a velocity oof 30 mm/sec. The car is placed on a platform which moves vertically at resonance speed having an amplitude of 10mm. Find the amplitude of the cararrow_forwardDetermine the differential equation of motion for the double pendulum shown in terms of12anduu where 12u and u are the horizontal distances of the masses from the leftmost verticalline that makes angle 1 from it. Find the natural frequencies, the ratios of the amplitudes, and thelocation of the nodes for the two modes of vibration. Assume m1=m2=m, and l1 =l2 = l=arrow_forward
- If we attach an object weighing 8 lb to a spring, it stretched the latter by 1 ft. We attach a weight of 16 lb to this spring and it comes to rest in its equilibrium position. We assume that there is no damping and an external force F(t) = cos 3t is applied to the system. If the system is put into motion with a downward initial velocity of 2 ft per sec, a. Determine the displacement of the object. [y(t) = - cos 4t + sin 4t + cos 3t ] 4. b. Find the natural frequency of the mass-spring system. [Natural Frequency: o = 4]arrow_forwardQ5/ A machine of mass 75 kg are mounted on springs and is fitted with a dashpot to damp out vibrations. There are three springs in parallel each of stiffness 10 N/mm and it is found that the amplitude of vibration diminishes from 38.4 mm to 6.4 mm in two complete oscillations. Assuming that the damping force varies as the velocity, determine (1) the resistance of the dashpot at unit velocity; (2) the ratio of the frequency of the damped vibration to the frequency of the undamped vibration; and (3) the periodic time of the damped vibration.arrow_forwardThe passenger car is modeled on a quarter-car model, in which case each wheel has a mass of 390 kg, in which case the specific frequency of the body is 1.1 Hz. The car is in a vibration tester that makes a vertical motion with an amplitude of 6 mm at a frequency of 6 Hz. Assume that D = 0. Calculate the maximum acceleration of the car body to one decimal place.arrow_forward
- The period of oscillation of a spring-and-mass system is 0.520 s and the amplitude is 5.06 cm. What is the magnitude of the acceleration at the point of maximum extension of the spring? m/s²arrow_forwardFast pls solve this question correctly in 5 min pls I will give u like for sure Anuarrow_forwardexplain each step brieflyarrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Elements Of Electromagnetics
Mechanical Engineering
ISBN:9780190698614
Author:Sadiku, Matthew N. O.
Publisher:Oxford University Press
Mechanics of Materials (10th Edition)
Mechanical Engineering
ISBN:9780134319650
Author:Russell C. Hibbeler
Publisher:PEARSON
Thermodynamics: An Engineering Approach
Mechanical Engineering
ISBN:9781259822674
Author:Yunus A. Cengel Dr., Michael A. Boles
Publisher:McGraw-Hill Education
Control Systems Engineering
Mechanical Engineering
ISBN:9781118170519
Author:Norman S. Nise
Publisher:WILEY
Mechanics of Materials (MindTap Course List)
Mechanical Engineering
ISBN:9781337093347
Author:Barry J. Goodno, James M. Gere
Publisher:Cengage Learning
Engineering Mechanics: Statics
Mechanical Engineering
ISBN:9781118807330
Author:James L. Meriam, L. G. Kraige, J. N. Bolton
Publisher:WILEY
Ch 2 - 2.2.2 Forced Undamped Oscillation; Author: Benjamin Drew;https://www.youtube.com/watch?v=6Tb7Rx-bCWE;License: Standard youtube license