Chapter 18, Problem 44CP

Review. A house roof is a perfectly flat plane that makes an angle θ with the horizontal. When its temperature changes, between T_i before dawn each day and T_k in the middle of each afternoon, the roof expands and contracts uniformly with a coefficient of thermal expansion α₁. Resting on the roof is a flat, rectangular metal plate with expansion coefficient α₂, greater than α₁. The length of the plate is L, measured along the slope of the roof. The component of the plate’s weight perpendicular to the roof is supported by a normal force uniformly distributed over the area of the plate. The coefficient of kinetic friction between the plate and the roof is μ_k. The plate is always at the same temperature as the roof, so we assume its temperature is continuously changing. Because of the difference in expansion coefficients, each bit of the plate is moving relative to the roof below it, except for points along a certain horizontal line running across the plate called the stationary line. If the temperature is rising, parts of the plate below the stationary line are moving down relative to the roof and feel a force of kinetic friction acting up the roof. Elements of area above the stationary line are sliding up the roof, and on them kinetic friction acts downward parallel to the roof. The stationary line occupies no area, so we assume no force of static friction acts on the plate while the temperature is changing. The plate as a whole is very nearly in equilibrium, so the net friction force on it must be equal to the component of its weight acting down the incline. (a) Prove that the stationary line is at a distance of

$\frac{L}{2}\left(1-\frac{\tan \theta }{{\mu }_k}\right)$

below the top edge of the plate. (b) Analyze the forces that act on the plate when the temperature is falling and prove that the stationary line is at that same distance above the bottom edge of the plate. (c) Show that the plate steps down the roof like an inchworm, moving each day by the distance

$\frac{L}{{\mu }_k}\left({\alpha }_2-{\alpha }_1\right)\left(T_h-T_c\right)\tan \theta$

(d) Evaluate the distance an aluminum plate moves each day if its length is 1.20 m, the temperature cycles between 4.00°C and 36.0°C, and if the roof has slope 18.5°, coefficient of linear expansion 1.50 × 10⁻⁵ (°C) ⁻¹, and coefficient of friction 0.420 with the plate. (e) What If? What if the expansion coefficient of the plate is less than that of the roof? Will the plate creep up the roof?

To determine

To show: The stationary line is at distance of $\frac{L}{2}\left(1-\frac{\tan \theta }{{\mu }_{\text{k}}}\right)$.

Answer to Problem 44CP

The distance at which stationary line lie is $\frac{L}{2}\left(1-\frac{\tan \theta }{{\mu }_{\text{k}}}\right)$.

Explanation of Solution

Given info: The angle made by the roof with the horizontal plane is $\theta$, the initial temperature is $T_{\text{c}}$, the final temperature is $T_{\text{c}}$, the coefficient of the thermal expansion is ${\alpha }_1$, the expansion coefficient of the metal plate is ${\alpha }_2$, the length of the plate is $L$ and the coefficient of kinetic friction between the plate and the roof is ${\mu }_{\text{k}}$.

Consider the figure given below.

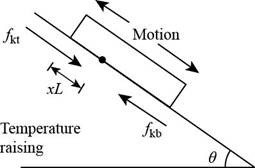
Figure 1

Consider that $xL$ represent the distance of the stationary line below the top edge of the plate.

The normal force on the lower part of the plane is,

$N=mg\left(1-x\right)\cos \theta$

Here,

$m$ is the mass of the plate.

$g$ is the acceleration due to gravity.

$x$ is the distance.

$\theta$ is the angle between plate and the roof.

The force due to gravity is,

$F_{\text{g}}=mg\sin \theta$

The equation for the kinematic friction force is,

$f_{\text{k}}=mg{\mu }_{\text{k}}\left(1-x\right)\cos \theta$

The equation for the downward force is,

$F=mg{\mu }_{\text{k}}x\cos \theta$

The force equation for the plate is,

$\begin{array}{c}{\displaystyle \sum F_{\text{x}}}=0\\ -mg{\mu }_{\text{k}}x\cos \theta +mg{\mu }_{\text{k}}\left(1-x\right)\cos \theta -mg\sin \theta =0\\ -2mg{\mu }_{\text{k}}x\cos \theta =mg\sin \theta -mg{\mu }_{\text{k}}\cos \theta \\ 2{\mu }_{\text{k}}x={\mu }_{\text{k}}-\tan \theta \end{array}$

Further, solve for $x$.

$\begin{array}{c}2{\mu }_{\text{k}}x={\mu }_{\text{k}}-\tan \theta \\ x=\frac{1}{2}-\frac{\tan \theta }{2{\mu }_{\text{k}}}\end{array}$

The distance of the stationary line below the top edge is,

$\begin{array}{c}xL=\frac{L}{2}-\frac{L\tan \theta }{2{\mu }_{\text{k}}}\\ =\frac{L}{2}\left(1-\frac{\tan \theta }{{\mu }_{\text{k}}}\right)\end{array}$

Conclusion:

Therefore, the distance at which stationary line lie is $\frac{L}{2}\left(1-\frac{\tan \theta }{{\mu }_{\text{k}}}\right)$.

To determine

To show: The stationary line is at that same distance above the bottom edge of the plate.

Answer to Problem 44CP

The stationary line is at that same distance above the bottom edge of the plate.

Explanation of Solution

Given info: The angle made by the roof with the horizontal plane is $\theta$, the initial temperature is $T_{\text{c}}$, the final temperature is $T_{\text{c}}$, the coefficient of the thermal expansion is ${\alpha }_1$, the expansion coefficient of the metal plate is ${\alpha }_2$, the length of the plate is $L$ and the coefficient of kinetic friction between the plate and the roof is ${\mu }_{\text{k}}$.

Consider the figure given below.

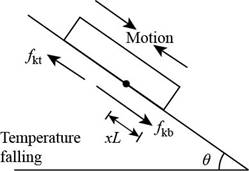
Figure 2

With the temperature falling, the plate contracts faster than the roof. The upper part slides down and feels an upward frictional force, $mg{\mu }_{\text{k}}\left(1-x\right)\cos \theta$. The lower part slides up and feels downward frictional force, $mg{\mu }_{\text{k}}x\cos \theta$.

Then the force equation remains same as in part (a) and the stationary line is above the bottom edge by,

$xL=\frac{L}{2}\left(1-\frac{\tan \theta }{{\mu }_{\text{k}}}\right)$

Conclusion:

Therefore, it is proved that the stationary line is at that same distance above the bottom edge of the plate.

To determine

To show: The plate steps down the roof like an inchworm moving each day by the distance $\frac{L}{{\mu }_{\text{k}}}\left({\alpha }_2-{\alpha }_1\right)\left(T_{\text{h}}-T_{\text{c}}\right)\tan \theta$.

Answer to Problem 44CP

The distance by which the plate steps down the roof like an inchworm moving each day is $\frac{L}{{\mu }_{\text{k}}}\left({\alpha }_2-{\alpha }_1\right)\left(T_{\text{h}}-T_{\text{c}}\right)\tan \theta$.

Explanation of Solution

Given info: The angle made by the roof with the horizontal plane is $\theta$, the initial temperature is $T_{\text{c}}$, the final temperature is $T_{\text{c}}$, the coefficient of the thermal expansion is ${\alpha }_1$, the expansion coefficient of the metal plate is ${\alpha }_2$, the length of the plate is $L$ and the coefficient of kinetic friction between the plate and the roof is ${\mu }_{\text{k}}$.

Consider the figure given below.

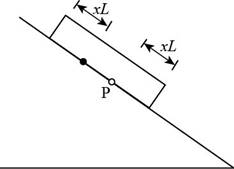
Figure 3

Consider the plate at dawn, as the temperature starts to rise. As in part (a), a line at distance $xL$ below the top edge of the plate stays stationary relative to the roof as long as the temperature rises.

In the above figure, the point $P$ on the plate at distance $xL$ above the bottom edge is destined to become the fixed point when the temperature starts falling. As the temperature rises, point $P$ on the plate slides down the roof relative to the upper fixed line from $\left(L-xL-xL\right)$ to $\left(L-xL-xL\right)\left(1+{\alpha }_2\Delta T\right)$.

The change in the length of the plate is,

$\Delta L_{\text{plate}}=\left(L-xL-xL\right){\alpha }_2\Delta T$

The change in the length of the roof is,

$\Delta L_{\text{roof}}=\left(L-xL-xL\right){\alpha }_1\Delta T$

The point on the roof originally under point $P$ on the plate slides down the roof relative to the upper fixed line from $\left(L-xL-xL\right)$ to $\left(L-xL-xL\right)\left(1+{\alpha }_1\Delta T\right)$ relative to the upper fixed line, a change of $\Delta L_{\text{roof}}$.

When the temperature drops, point $P$ remains stationary on the roof while the roof contracts, pulling point $P$ back by approximately $\Delta L_{\text{roof}}$. Thus relative to the upper fixed line, point $P$ is moved down the roof $\Delta L_{\text{plate}}-\Delta L_{\text{roof}}$.

The displacement for a day is,

$\begin{array}{c}\Delta L_{\text{plate}}-\Delta L_{\text{roof}}=\left({\alpha }_2-{\alpha }_1\right)\left(L-xL-xL\right)\Delta T\\ =\left({\alpha }_2-{\alpha }_1\right)\left(L-2xL\right)\Delta T\end{array}$

Substitute $\frac{L}{2}\left(1-\frac{\tan \theta }{{\mu }_{\text{k}}}\right)$ for $xL$ in the above expression.

$\begin{array}{c}\Delta L_{\text{plate}}-\Delta L_{\text{roof}}=\left({\alpha }_2-{\alpha }_1\right)\left(L-2\left(\frac{L}{2}\right)\left(1-\frac{\tan \theta }{{\mu }_{\text{k}}}\right)\right)\Delta T\\ =\left({\alpha }_2-{\alpha }_1\right)\left(L-L\left(1-\frac{\tan \theta }{{\mu }_{\text{k}}}\right)\right)\left(T_{\text{h}}-T_{\text{c}}\right)\\ =\left({\alpha }_2-{\alpha }_1\right)\left(L-L+\frac{L\tan \theta }{{\mu }_{\text{k}}}\right)\left(T_{\text{h}}-T_{\text{c}}\right)\\ =\frac{L}{{\mu }_{\text{k}}}\left({\alpha }_2-{\alpha }_1\right)\left(T_{\text{h}}-T_{\text{c}}\right)\tan \theta \end{array}$

Conclusion:

Therefore, the distance by which the plate steps down the roof like an inchworm moving each day is $\frac{L}{{\mu }_{\text{k}}}\left({\alpha }_2-{\alpha }_1\right)\left(T_{\text{h}}-T_{\text{c}}\right)\tan \theta$.

To determine

The distance an aluminum plate moves each day.

Answer to Problem 44CP

The distance an aluminum plate moves each day is $\text{0}\text{.275}\text{mm}$.

Explanation of Solution

Given info: The angle made by the roof with the horizontal plane is $\theta$, the initial temperature is $T_{\text{c}}$, the final temperature is $T_{\text{c}}$, the coefficient of the thermal expansion is ${\alpha }_1$, the expansion coefficient of the metal plate is ${\alpha }_2$, the length of the plate is $L$ and the coefficient of kinetic friction between the plate and the roof is ${\mu }_{\text{k}}$.

The length of the plate is $1.20\text{m}$, the initial temperature is $4.00°\text{C}$, the final temperature is $36.0°\text{C}$, the angle made by the roof with the horizontal plane is $18.5°$, the coefficient of linear expansion is $1.50\times {10}^{-5}°{\text{C}}^{-1}$ and the coefficient of kinetic friction is $0.420$.

The coefficient of linear expansion for aluminum is $24\times {10}^{-6}°{\text{C}}^{-1}$.

The formula for the displacement for a day is,

$\Delta L_{\text{plate}}-\Delta L_{\text{roof}}=\frac{L}{{\mu }_{\text{k}}}\left({\alpha }_2-{\alpha }_1\right)\left(T_{\text{h}}-T_{\text{c}}\right)\tan \theta$

Substitute $1.20\text{m}$ for $L$, $0.420$ for ${\mu }_{\text{k}}$, $1.50\times {10}^{-5}°{\text{C}}^{-1}$ for ${\alpha }_1$, $24\times {10}^{-6}°{\text{C}}^{-1}$ for ${\alpha }_2$, $4.00°\text{C}$ for $T_{\text{c}}$, $36.0°\text{C}$ for $T_{\text{h}}$ and $18.5°$ for $\theta$ in above equation.

$\begin{array}{c}\Delta L_{\text{plate}}-\Delta L_{\text{roof}}=\left(\frac{1.20\text{m}}{0.420}\right)\left(24\times {10}^{-6}°{\text{C}}^{-1}-1.50\times {10}^{-5}°{\text{C}}^{-1}\right)\left(36.0°\text{C}-4.00°\text{C}\right)\tan \left(18.5°\right)\\ =2.75\times {10}^{-4}\text{m}\\ =\text{0}\text{.275}\text{mm}\end{array}$

Conclusion:

Therefore, the distance an aluminum plate moves each day is $\text{0}\text{.275}\text{mm}$.

To determine

To explain: The effect on the plate if the expansion coefficient of the plate is less than the expansion coefficient of the roof.

Answer to Problem 44CP

The plate creeps down the roof each day by an amount given by $\frac{L}{{\mu }_{\text{k}}}\left({\alpha }_1-{\alpha }_2\right)\left(T_{\text{c}}-T_{\text{h}}\right)\tan \theta$.

Explanation of Solution

Given info: The angle made by the roof with the horizontal plane is $\theta$, the initial temperature is $T_{\text{c}}$, the final temperature is $T_{\text{c}}$, the coefficient of the thermal expansion is ${\alpha }_1$, the expansion coefficient of the metal plate is ${\alpha }_2$, the length of the plate is $L$ and the coefficient of kinetic friction between the plate and the roof is ${\mu }_{\text{k}}$.

If ${\alpha }_2<{\alpha }_1$, the forces of the friction reverse direction relative to part (a) and part (b) because the roof expands more than the plate as the temperature rises and less as the temperature falls.

The figure I, applies to the temperature falling and figure II applies to temperature rising. A point on the plate $xL$ from the top of the plate moves upward from lower fixed line by $\Delta L_{\text{plate}}$, and when the temperature drops, the upper fixed line of the plates is carried down the roof by $\Delta L_{\text{roof}}$. So the net change in the plate’s position is $\Delta L_{\text{roof}}-\Delta L_{\text{plate}}$, where $\Delta L_{\text{roof}}>\Delta L_{\text{plate}}$.

The plate creeps down the roof each day by an amount given by,

$\begin{array}{c}\Delta L_{\text{roof}}-\Delta L_{\text{plate}}=\left({\alpha }_1-{\alpha }_2\right)\left(L-L\left(1-\frac{\tan \theta }{{\mu }_{\text{k}}}\right)\right)\left(T_{\text{c}}-T_{\text{h}}\right)\\ =\left({\alpha }_1-{\alpha }_2\right)\left(L-L+\frac{L\tan \theta }{{\mu }_{\text{k}}}\right)\left(T_{\text{c}}-T_{\text{h}}\right)\\ =\frac{L}{{\mu }_{\text{k}}}\left({\alpha }_1-{\alpha }_2\right)\left(T_{\text{c}}-T_{\text{h}}\right)\tan \theta \end{array}$

Conclusion:

Therefore, the plate creeps down the roof each day by an amount given by $\frac{L}{{\mu }_{\text{k}}}\left({\alpha }_1-{\alpha }_2\right)\left(T_{\text{c}}-T_{\text{h}}\right)\tan \theta$.