Engineering Mechanics: Dynamics (14th Edition)
14th Edition
ISBN: 9780133915389
Author: Russell C. Hibbeler
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 17.4, Problem 66P
Show that IGα may be eliminated by moving the
Expert Solution & Answer
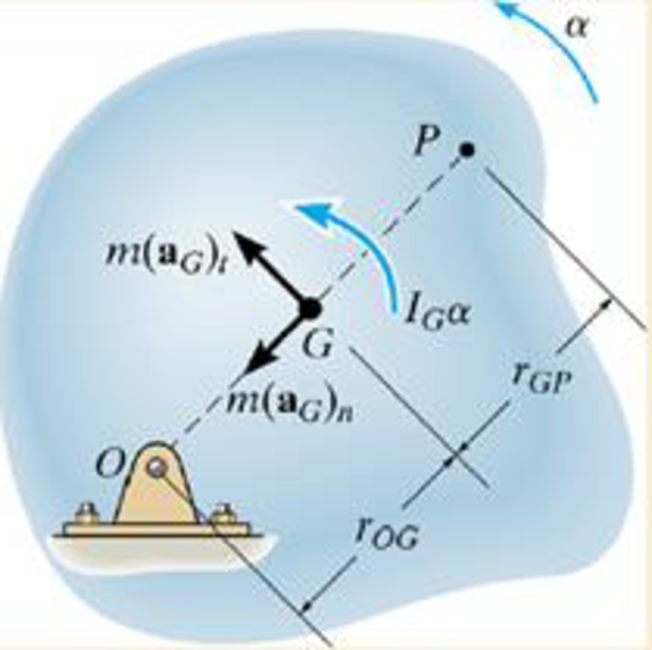
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
ONLY HANDWRITTEN please
A square panel with a mass of 12 kg is suspended from point C by two ropes at points A and B. If the
rope at B is suddenly cut, calculate the tension I in rope A immediately after the cut. The moment
of inertia with respect to the center of mass is I = {mb².
C
45°
45
A
B
b
b
(Ctrl)
The centroidal mass moment of inertia ofthe pulley assembly is 20 ft-lb-s2. Determine (a) the tension in the cordsupporting 161-lb block , (b)the tension supporting the 322-lb block, and (c) the angularacceleration of the pulley system .Hint: Determine first the direction ofmotion, i.e. will block A move up ordown?
Chapter 17 Solutions
Engineering Mechanics: Dynamics (14th Edition)
Ch. 17.1 - The rod's density end cross-sectional area. A are...Ch. 17.1 - Determine the mass of the cylinder end its moment...Ch. 17.1 - The nag has a mass m.Ch. 17.1 - Determine the radius of gyration kx. The density...Ch. 17.1 - The specific weight of the material is = 380...Ch. 17.1 - Determine the moment of inertia Iz and express the...Ch. 17.1 - Determine the moment of inertia Ix and express the...Ch. 17.1 - Defending the moment of inertia Iy and express the...Ch. 17.1 - Express the result in terms of the mass m of the...Ch. 17.1 - Determine me radius of gyration of the pendulum...
Ch. 17.1 - Determine the mass moment of inertia of the...Ch. 17.1 - Determine the moment of inertia of the solid steel...Ch. 17.1 - Determine the wheels moment of inertia about an...Ch. 17.1 - If the large ring, small ring and each of the...Ch. 17.1 - The thin plate has a hole in its center its...Ch. 17.1 - The material has a mass per unit area of 20 kg/m2.Ch. 17.1 - The block has a mass of 3 kg and the semicylinder...Ch. 17.1 - The block has a mass of 3 kg and the semicylinder...Ch. 17.1 - The material has a specific weight = 90 lb/ft3.Ch. 17.1 - Prob. 20PCh. 17.1 - Determine the location y of the center of mass G...Ch. 17.1 - The material is steel having a density of = 7.85...Ch. 17.1 - The material is steel having a density of = 7.85...Ch. 17.3 - Draw the free-body and kinetic diagrams of the...Ch. 17.3 - Draw the free-body and kinetic diagrams of the...Ch. 17.3 - Determine the acceleration of the can and the...Ch. 17.3 - If the 80-kg cabinet is allowed to roll down the...Ch. 17.3 - Determine the maximum acceleration of the frame...Ch. 17.3 - Also what is the corresponding normal reaction on...Ch. 17.3 - Determine the tension developed in the rods and...Ch. 17.3 - If it is subjected to a couple moment M = 450 N ...Ch. 17.3 - Determine how far the door moves in 25, starting...Ch. 17.3 - Determine the constant force F that must be...Ch. 17.3 - Initially at take-off the engines provide a thrust...Ch. 17.3 - If it starts from rest it causes the rear wheels...Ch. 17.3 - If the winch at B draws in the cable with an...Ch. 17.3 - Determine the greatest acceleration of the...Ch. 17.3 - Determine the internal axial, shear, and...Ch. 17.3 - If the coefficient of kinetic friction between the...Ch. 17.3 - Determine the reactions at both the wheels at A...Ch. 17.3 - Also, what is the acceleration of the cart? The...Ch. 17.3 - If it is subjected to a horizontal force of P =...Ch. 17.3 - Determine its initial acceleration if a man pushes...Ch. 17.3 - Determine the initial acceleration of a desk when...Ch. 17.3 - Determine the maximum force P that can be applied...Ch. 17.3 - Determine the maximum force P that can be applied...Ch. 17.3 - If it is released from rest, determine the...Ch. 17.3 - It is carried on a truck as shown. Determine the...Ch. 17.3 - It is carried on a truck as shown. If the truck...Ch. 17.3 - Determine the smallest acceleration that will...Ch. 17.3 - The coefficients of static and kinetic friction...Ch. 17.3 - If the collar is given a constant acceleration of...Ch. 17.3 - If it is supported by the cable AB and hinge at C,...Ch. 17.3 - If it is supported by the cable AB and hinge at C,...Ch. 17.3 - If the acceleration is a = 20 ft/s2, determine the...Ch. 17.3 - If h = 3 ft, determine the snowmobiles maximum...Ch. 17.3 - If the carts mass is 30 kg and it is subjected to...Ch. 17.3 - The uniform rod BC has a mass of 15 kg.Ch. 17.3 - If the acceleration of the truck is at = 0.5 m/s2,...Ch. 17.3 - If the angle = 30, determine the acceleration of...Ch. 17.3 - Determine the largest initial angular acceleration...Ch. 17.3 - Determine the initial friction and normal force of...Ch. 17.3 - Determine the largest initial angular acceleration...Ch. 17.3 - Determine the normal force NE, shear force VE, and...Ch. 17.4 - If the wheel starts from rest determine its...Ch. 17.4 - Determine the angular velocity of the disk when t...Ch. 17.4 - Determine the tangential and normal components of...Ch. 17.4 - Determine the tangential and normal components or...Ch. 17.4 - Determine the horizontal and vertical components...Ch. 17.4 - If the rod has a counterclockwise angular velocity...Ch. 17.4 - If the wheel is subjected to a moment M = (5t) N ...Ch. 17.4 - Determine its initial angular acceleration and the...Ch. 17.4 - If it is released from rest when = 0. determine...Ch. 17.4 - If it is released from rest in the position shown,...Ch. 17.4 - The reel rests on rollers at A and B and has a...Ch. 17.4 - The spring has a stiffness k = 5 lb ft/rad, so...Ch. 17.4 - The spring has a stiffness k = 5 lb ft/rad, so...Ch. 17.4 - If a force of F=(142)N, where is in radians, is...Ch. 17.4 - If no slipping occurs between them determine the...Ch. 17.4 - Show that IG may be eliminated by moving the...Ch. 17.4 - Treat the beam as a uniform slender rod.Ch. 17.4 - It consists of a 100-kg steel plate AC and a...Ch. 17.4 - It is pin supported at both ends by two brackets...Ch. 17.4 - It is pin supported at both ends by two brackets...Ch. 17.4 - Determine its angular velocity when t = 2 s...Ch. 17.4 - If it is placed on the ground for which the...Ch. 17.4 - Compute the time needed to unravel 5 m of cable...Ch. 17.4 - If the rotor always maintains a constant clockwise...Ch. 17.4 - It is originally spinning at = 40 rad/s. If it is...Ch. 17.4 - It is pin supported at both ends by two brackets...Ch. 17.4 - Disk E has a weight of 60 lb and is initially at...Ch. 17.4 - If the cylinders are released from rest, determine...Ch. 17.4 - If the pulley can be treated as a disk of mass 3...Ch. 17.4 - If the pulley can be treated as a disk of mass M,...Ch. 17.4 - Assume that the board is uniform and rigid, and...Ch. 17.4 - At the instant the rolor is horizontal it has an...Ch. 17.4 - Determine the initial tending moment at the fixed...Ch. 17.4 - Movement is controlled by the electromagnet E,...Ch. 17.4 - If it is rotating in the vertical plane at a...Ch. 17.4 - Determine the angular acceleration of the rod and...Ch. 17.4 - Determine the horizontal and vertical components...Ch. 17.4 - Determine the horizontal and vertical components...Ch. 17.5 - If the powder burns at a constant rate of 20 g/s...Ch. 17.5 - Determine the acceleration of the bars mass center...Ch. 17.5 - Determine the acceleration of its mass center and...Ch. 17.5 - When the wheel is subjected to the couple moment,...Ch. 17.5 - Determine the angular acceleration of the sphere...Ch. 17.5 - If the couple moment is applied to the spool and...Ch. 17.5 - If the rod is released from rest at = 0,...Ch. 17.5 - rolls without slipping, show that when moments are...Ch. 17.5 - If it is initially at rest and is subjected to a...Ch. 17.5 - The uniform 150-lb beam is initially at rest when...Ch. 17.5 - If the coefficients of static and kinetic friction...Ch. 17.5 - If the coefficients of static and kinetic friction...Ch. 17.5 - If the coefficients of static and kinetic friction...Ch. 17.5 - Solve Prob.17-96 if the cord and force P = 50 N...Ch. 17.5 - If the coefficients of static and kinetic friction...Ch. 17.5 - If a horizontal force of F = 80 N is applied to...Ch. 17.5 - If slipping does not occur, determine the rings...Ch. 17.5 - Neglect the thickness of the ring.Ch. 17.5 - Using a collar of negligible mass, its end A is...Ch. 17.5 - If the pin is connected to a track which is giver...Ch. 17.5 - Assume the roller to be a uniform cylinder and...Ch. 17.5 - Also, find the angular acceleration of the roller....Ch. 17.5 - Determine the bars initial angular acceleration...Ch. 17.5 - Solve Prob.17-106 if the roller is removed and the...Ch. 17.5 - If the coefficient of static friction at A is s, =...Ch. 17.5 - If the truck has an acceleration of 3 m/s2...Ch. 17.5 - A cord is wrapped around the periphery of the disk...Ch. 17.5 - If the coefficient of static friction at A is s =...Ch. 17.5 - At this instant the center of gravity of the...Ch. 17.5 - Determine the initial angular acceleration of the...Ch. 17.5 - Determine the time before it starts to roll...Ch. 17.5 - If they are released from rest determine the...Ch. 17.5 - Determine the normal force which the path exerts...Ch. 17.5 - If it is originally at rest while being supported...Ch. 17.5 - If the pin support at A suddenly fails, determine...Ch. 17.5 - Determine its angular acceleration.Ch. 17.5 - If the coefficient of kinetic friction between the...Ch. 17.5 - Determine the normal reactions at each of the...Ch. 17.5 - Determine the internal axial force Ex, shear force...Ch. 17.5 - Determine the maximum acceleration it can have if...Ch. 17.5 - The roil rest against a wall for which the...Ch. 17.5 - Determine the magnitude of force F and the initial...Ch. 17.5 - Compute the reaction at the pin O just after the...Ch. 17.5 - if the coefficient of kinetic friction at the...Ch. 17.5 - The coefficient of kinetic friction is A = 0.3.
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, mechanical-engineering and related others by exploring similar questions and additional content below.Similar questions
- Two balls with masses M and m are connected by a rigid rod of length L and negligible mass as shown. For an axis perpendicular to the rod, (a) show that the system has the minimum moment of inertia when the axis passes through the center of mass. (b) Show that this moment of inertia is I = μL2, where μ = mM/(m + M).arrow_forwardThe 24-kg uniform thin hollow square plate is pinned at point O, and its side L = 0.3 m. Determine its mass moment of inertia / (in kg•m²) about point O. Please pay attention: the numbers may change since they are randomized. Your answer must include 2 places after the decimal point. Take g = 9.81 m/s². M Your Answer: Answerarrow_forwardShow the complete solution.arrow_forward
- Assuming small displacements, write the equation of motion for the system shown below in terms of x₁, x₂, х1, х2, and 0. Assume that the lever has a mass moment of inertia about the pivot of Im. K₁ 000 M₁ K₂ 000 777 -fa(1) M₂arrow_forwardThe following masses m, are located at the given points P₁ : m₁ = 6, P₁(1, −2) m₂ = 5, P₂(3, 4) m3 = 1, P3(−3,−7) m₁ = 4, P₁(6,−1) Find the moments Mx, My, and the x and y-coordinates of the center of mass of the system. Mx My = = I- ▶ x-coordinate of the center of mass: x = y-coordinate of the center of mass: y = B ▶arrow_forwardCan anyone help me with this questionarrow_forward
- The rigid body (slab) has a mass m and rotates with an angular velocity es about an axis passing through the fixed point 0. Show that the momenta of all the particles composing the body can be represented by a single vector having a magnitude mvg and acting through point P, called the center of percussion, which lies at a distance TPIG - ka/rajo from the mass center G. Here kg is the radius of gyration of the body, computed about an axis perpendicular to the plane of motion and passing through G.arrow_forward3. The pendulum consists of a 5 kg plate and a 3 kg slender rod. Determine the radius of gyration of the pendulum about an axis perpendicular to the plane of movement and passing through point G (the mass center for the pendulum). 2 m + 0.5 m Garrow_forwardh y g(x) density p = 800 kg m³ Determine the cone's radius of gyration about the x-axis. 2h x An engineering student has modelled a truncated cone in CAD software by rotating the coloured area about the x-axis. The y-coordinate can be described by the equation g(x) = + 1 and the cup has constant 6 The cone has dimensions h = 1 m and l = 6 m. Xarrow_forward
- The homogeneous bars have a mass as follows: bar AC has a mass of 7 kg, bar ABhas a mass of 10 kg, and rod BD has a mass of 2 kg. In the drawn position, therod AC has an angular velocity of 4 rad/s and an angular acceleration of 2 rad/s2, both clockwise.Determine the magnitude of the moment M acting on the member AC. Give all the equations neededto solve this question without calculating itarrow_forwardFind the centre of mass of the object below. Let the lengths be: d1 = 160mm, d2 = 270 mm, d3= 200 mm, d4 = 210 mm, d5 = 300mm, d6 = 240mm.arrow_forwardIf the 15 kg bar has a center of mass at G, calculate the resulting moment at point O.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
International Edition---engineering Mechanics: St...Mechanical EngineeringISBN:9781305501607Author:Andrew Pytel And Jaan KiusalaasPublisher:CENGAGE L
International Edition---engineering Mechanics: St...
Mechanical Engineering
ISBN:9781305501607
Author:Andrew Pytel And Jaan Kiusalaas
Publisher:CENGAGE L
Fluid Mechanics - Viscosity and Shear Strain Rate in 9 Minutes!; Author: Less Boring Lectures;https://www.youtube.com/watch?v=_0aaRDAdPTY;License: Standard youtube license