Chapter 17, Problem 72CP

(a)

To determine

Sketch the force diagram showing that the force exerted due to the pressure of gas on either side of the element.

Answer to Problem 72CP

The force diagram is given below.

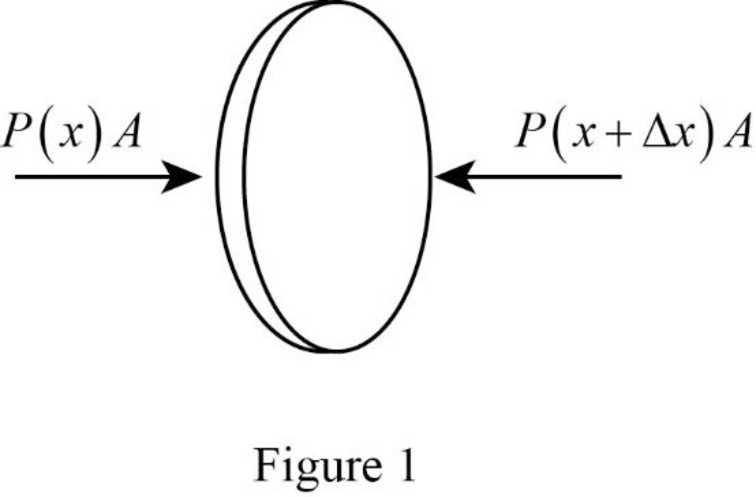
Explanation of Solution

The figure 1 below is the force diagram, which shows that the force exerted on the left and right surface due to the pressure of the gas on either side of the element.

(b)

To determine

Show that $-\frac{\partial \left(\Delta P\right)}{\partial x}A\Delta x=\rho a\Delta x\frac{{\partial }^{2}s}{\partial t^2}$.

Answer to Problem 72CP

Through calculation it is obtained that $-\frac{\partial \left(\Delta P\right)}{\partial x}A\Delta x=\rho a\Delta x\frac{{\partial }^{2}s}{\partial t^2}$.

Explanation of Solution

Consider $P\left(x\right)$ as the absolute pressure as a function of $x$.

The net force acting on the element is the difference of the force acting on the either sides due to the pressure of the gas.

  $\left[-\Delta P\left(x+\Delta x\right)+\Delta P\left(x\right)\right]A=-\frac{\partial \Delta P}{\partial x}\Delta xA$                                                                  (I)

The force acting on the surface is.

  $F=\Delta ma$                  (II)

Here, $\Delta m$ is the mass of the air, and $a$ is the acceleration.

Write the expression for mass in terms of volume and density.

  $\begin{array}{c}\Delta m=\rho \Delta V\\ =\rho A\Delta x\end{array}$                                                                                                            (III)

Substitute, $\frac{{\partial }^{2}s}{\partial t^2}$ for $a$ , and $\rho A\Delta x$ for $\Delta m$ in equation (II).

  $F=\rho A\Delta x\frac{{\partial }^{2}s}{\partial t^2}$                                                                                                        (IV)

Conclusion:

Equate equation (IV) and (I).

  $-\frac{\partial \Delta P}{\partial x}\Delta xA=\rho A\Delta x\frac{{\partial }^{2}s}{\partial t^2}$                                                                                          (V)

Therefore, $-\frac{\partial \Delta P}{\partial x}\Delta xA=\rho A\Delta x\frac{{\partial }^{2}s}{\partial t^2}$ this equation shows that force exerted on surfaces due to the pressure of gas on the either sides of the element.

(c)

To determine

Derive $\frac{B}{\rho }\frac{{\partial }^{2}S}{\partial x^2}=\frac{{\partial }^{2}S}{\partial t^2}$.

Answer to Problem 72CP

It is derived that $\frac{B}{\rho }\frac{{\partial }^{2}S}{\partial x^2}=\frac{{\partial }^{2}S}{\partial t^2}$.

Explanation of Solution

Consider equation (V).

  $\begin{array}{l}-\frac{\partial \Delta P}{\partial x}\Delta xA=\rho A\Delta x\frac{{\partial }^{2}s}{\partial t^2}\\ -\frac{\partial \Delta P}{\partial x}=\rho \frac{{\partial }^{2}s}{\partial t^2}\end{array}$                                                                                          (VI)

Substitute, $B\frac{\partial s}{\partial x}$ for $\Delta P$ in equation (VI).

  $\begin{array}{c}-\frac{\partial \left(B\frac{\partial s}{\partial x}\right)}{\partial x}=\rho \frac{{\partial }^{2}s}{\partial t^2}\\ \frac{B}{\rho }\frac{{\partial }^{2}s}{\partial x^2}=\frac{{\partial }^{2}s}{\partial t^2}\end{array}$                                                                                                (VII)

Conclusion:

Therefore, it is derived that $\frac{B}{\rho }\frac{{\partial }^{2}S}{\partial x^2}=\frac{{\partial }^{2}S}{\partial t^2}$.

(d)

To determine

Prove that $s\left(x,t\right)=s_{\text{max}}\cos \left(kx-\omega t\right)$ satisfies wave equation.

Answer to Problem 72CP

The function $s\left(x,t\right)=s_{\text{max}}\cos \left(kx-\omega t\right)$ satisfies wave equation.

Explanation of Solution

Consider the given function.

  $s\left(x,t\right)=s_{\text{max}}\cos \left(kx-\omega t\right)$         (VIII)

Differentiate equation (VIII) with respect to $x$.

  $\frac{\partial s\left(x,t\right)}{\partial x}=-k{s}_{\text{max}}\sin \left(kx-\omega t\right)$                                                                                 (IX)

Differentiate equation (IX) with respect to $x$.

  $\frac{{\partial }^{2}s\left(x,t\right)}{\partial x^2}=-k^2{s}_{\text{max}}\cos \left(kx-\omega t\right)$                                                                            (X)

Differentiate equation (VIII) with respect to $t$.

  $\frac{\partial s\left(x,t\right)}{\partial t}=\omega s_{\text{max}}\sin \left(kx-\omega t\right)$                                                                                 (XI)

Differentiate equation (XI) with respect to $t$.

  $\frac{{\partial }^{2}s\left(x,t\right)}{\partial t^2}=-{\omega }^2{s}_{\text{max}}\cos \left(kx-\omega t\right)$                                                                          (XII)

Substitute, equation (X) and (XII) in equation (VII).

  $\begin{array}{c}\frac{B}{\rho }\left(-k^2{s}_{\text{max}}\cos \left(kx-\omega t\right)\right)=-{\omega }^2{s}_{\text{max}}\cos \left(kx-\omega t\right)\\ \frac{B}{\rho }{k}^2={\omega }^2\\ \frac{\omega }{k}=\sqrt{\frac{B}{\rho }}\end{array}$                                               (XIII)

Equation (XIII) shows that the function $s\left(x,t\right)=s_{\text{max}}\cos \left(kx-\omega t\right)$ satisfies wave equation.

Conclusion:

Therefore, unction $s\left(x,t\right)=s_{\text{max}}\cos \left(kx-\omega t\right)$ satisfies wave equation.