
Concept explainers
Given that Fourier coefficients a0, an, and bn of the waveform in Fig. 17.47. Plot the amplitude and phase spectra.
Figure 17.47
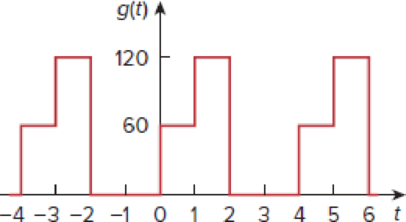
Find the Fourier coefficients
Answer to Problem 3P
The Fourier coefficients
Explanation of Solution
Given data:
Refer to Figure 17.47 in the textbook.
Formula used:
Write the expression to calculate the fundamental angular frequency.
Here,
Write the expression to calculate the dc component of the function
Write the expression to calculate Fourier coefficients
Here,
Calculation:
The given waveform is drawn as Figure 1.
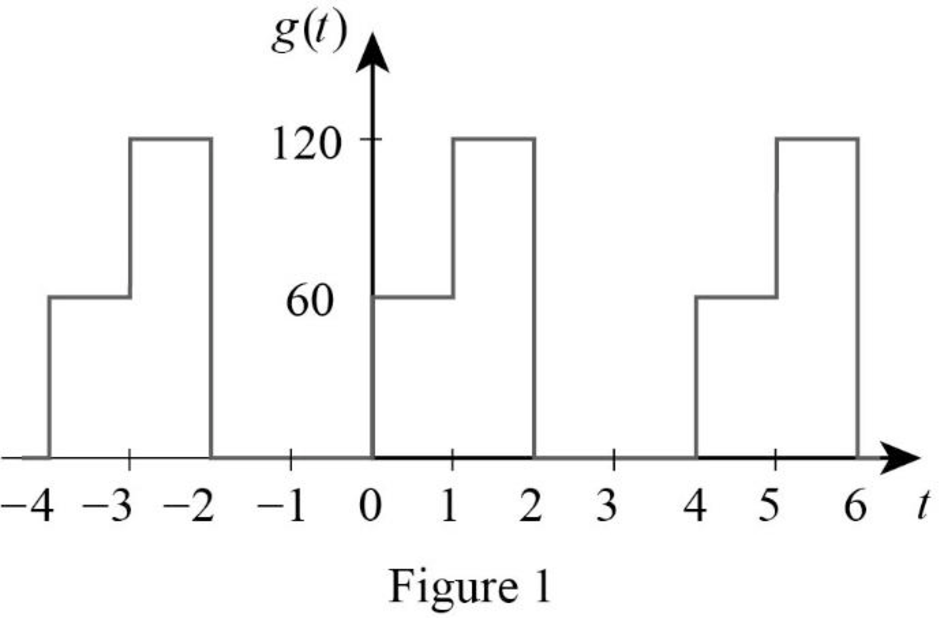
Refer to the Figure 1. The Fourier series function of the waveform is defined as,
The time period of the function in Figure 1 is,
Substitute
Substitute
Simplify the above equation to find
Substitute
Simplify the above equation to find
Simplify the above equation to find
From above equation, it is clear that
For odd
Substitute
Substitute
Substitute
Substitute
Substitute
Simplify the above equation to find
Simplify the above equation to find
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Write the expression to calculate the amplitude spectra of the signal.
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
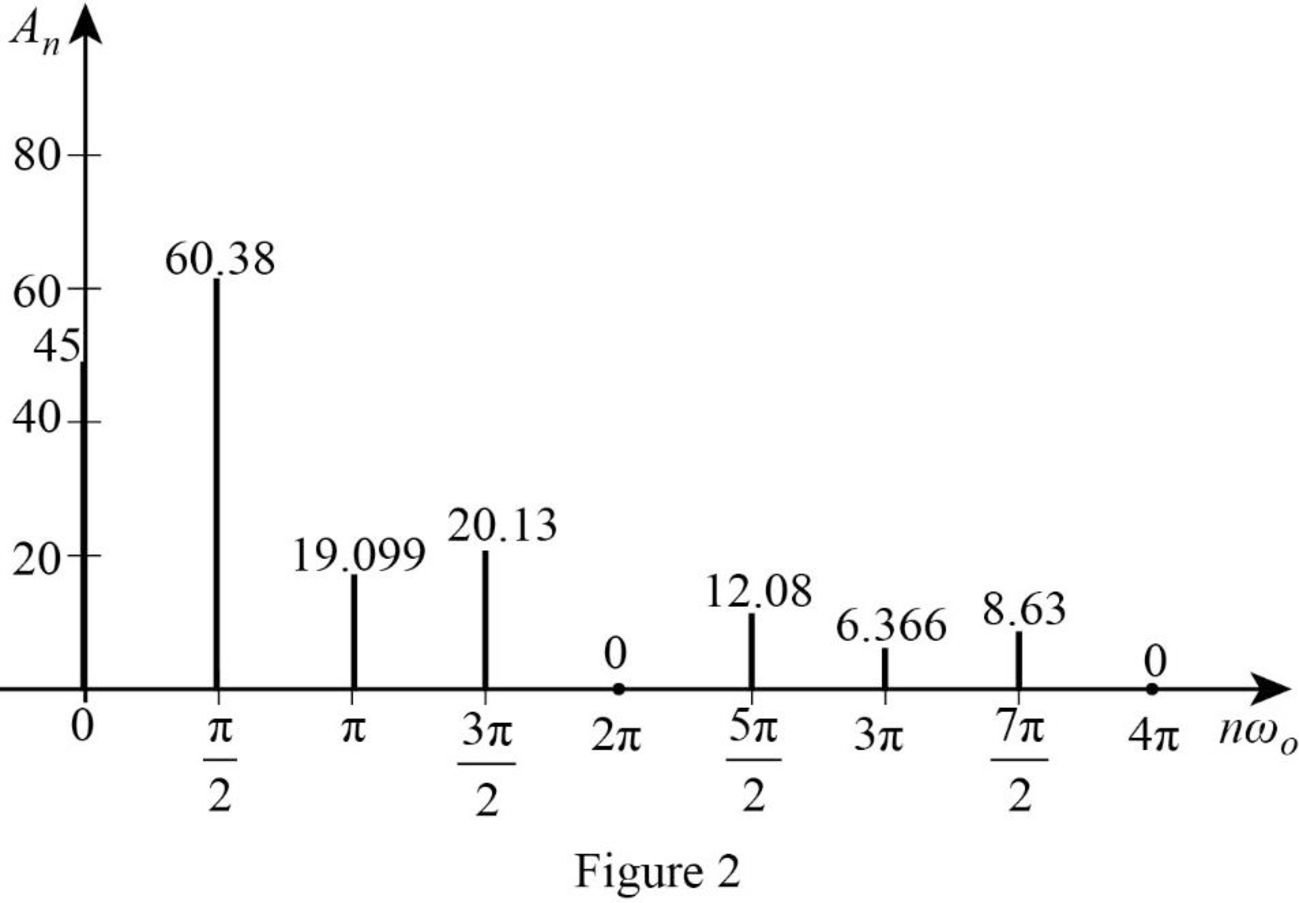
From above calculations, the amplitude spectrum of the waveform in Figure 1 is drawn as Figure 2.
Write the expression to calculate the phase spectra of the signal.
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
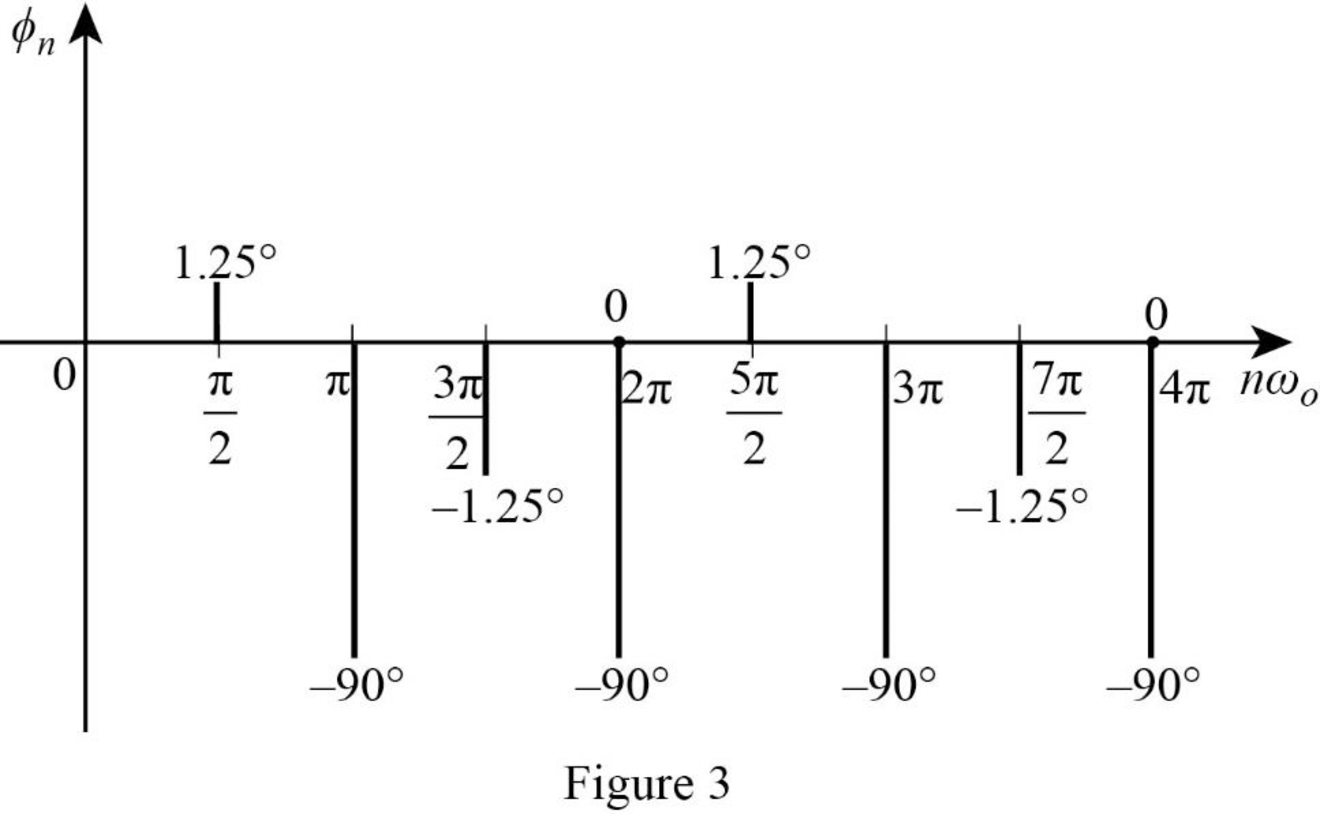
From above calculations, the phase spectrum of the waveform in Figure 1 is drawn as Figure 3.
Conclusion:
Thus, the Fourier coefficients
Want to see more full solutions like this?
Chapter 17 Solutions
EBK FUNDAMENTALS OF ELECTRIC CIRCUITS
- 15) Complex numbers 21 and 22 are given by Δ Δ Δ Z₁ = 21-60° 22 = 5/45° Determine in polar form: Z, Z₂ b) 21/22 Z₁ C) Z, Z₂ dz 2 zz Z f) JZ ₂ 9) z, (z₂-z₁) * ~22/(Z1+Zz) FAAAAAA Aarrow_forwardform: Express The following Complex numbers in rectangular № 2, b) Z₂ = -3e-jπ/4 c) 23 = √ 3 e d 24 11 -j 25 = ==J 3 -4 2 -j3π/4 f) 26 = (2 + j) 9) 2₂ = (3-j2)³ g D 27 AAA D A 35arrow_forward0) Express The following complex numbers in polar form: az₁ = 3+ j4 2 b) 2₂ = -6+j8 C) 23 = 6j4 Z4=j2 d) 24 = j2 e) 25 = (2+ j)² 3 4) 26 = (3-j2) ³ JZ7 = (1+j) ½/2 27 D D D D D AA D AALarrow_forward
- 21) Determine. The phasor counterparts of the following sinusoidal functions: (a) V₁ (t) = 4 cos (377-30°) V (B) V₂ (t) = -2sin (8T x 10"+ + 18°) V e) V3 (t) = 3 sin (1000 + + 53°)-4c05 (1000 t -17°) v AAA AAAAAarrow_forwardI need help with this problem and an explanation of the solution for the image described below. (Introduction to Signals and Systems)arrow_forwardTutorial - Design of Common-Gate (CG) Amplifier Design a common-gate NMOS amplifier with the following parameters: Supply Voltage (VDD): 10 V ⚫Threshold Voltage (Vth): 2 V •Overdrive Voltage (Vov) = VGS-Vth: 1 V • Desired Voltage Gain Av: 10 V/V • Transconductance gm: to be determined •Ensure that the NMOS operates in the saturation region. ⚫ Design Vos to ensure saturation and enough voltage swing. C₁ Vin +VDD RD C₂ V out Rs WI RLarrow_forward
- NEED HANDWRITTEN SOLUTION DO NOT USE CHATGPT OR AIarrow_forwardDetermine the response y(n), n≥0 of the system described by the second order difference equation: y(n)-4y(n-1)+4y(n-2)=x(n)-x(n-1) when the input is x(n)=(−1)" u(n) and the initial conditions are y(-1)=y(-2)=0.arrow_forwardConsider a Continuous- time LTI System described by y' (+)+ nycH) = x() find yet for a) x(+)o ē+4(H) b) X(+) = u(+). c) X(H= 5(+)arrow_forward
- Find the Thevenin equivalent representation of the circuit given to the left of the nodes a and b. Find Vth and Rth and draw the equivalent Thevenin circuit. For Rth use a 1 volt test source as your method.arrow_forwardR(s) + E(s) 100(s+2)(s+6) s(s+3)(s+4) C(s)arrow_forwardEXAMPLE 3.6 Determine the signal pз(t)=p₁(2t-1), if the signal p₁(t) is defined as follows: P₁(t)= 1-|t| |t|≤1 {" 0, |t|>1arrow_forward
 Introductory Circuit Analysis (13th Edition)Electrical EngineeringISBN:9780133923605Author:Robert L. BoylestadPublisher:PEARSON
Introductory Circuit Analysis (13th Edition)Electrical EngineeringISBN:9780133923605Author:Robert L. BoylestadPublisher:PEARSON Delmar's Standard Textbook Of ElectricityElectrical EngineeringISBN:9781337900348Author:Stephen L. HermanPublisher:Cengage Learning
Delmar's Standard Textbook Of ElectricityElectrical EngineeringISBN:9781337900348Author:Stephen L. HermanPublisher:Cengage Learning Programmable Logic ControllersElectrical EngineeringISBN:9780073373843Author:Frank D. PetruzellaPublisher:McGraw-Hill Education
Programmable Logic ControllersElectrical EngineeringISBN:9780073373843Author:Frank D. PetruzellaPublisher:McGraw-Hill Education Fundamentals of Electric CircuitsElectrical EngineeringISBN:9780078028229Author:Charles K Alexander, Matthew SadikuPublisher:McGraw-Hill Education
Fundamentals of Electric CircuitsElectrical EngineeringISBN:9780078028229Author:Charles K Alexander, Matthew SadikuPublisher:McGraw-Hill Education Electric Circuits. (11th Edition)Electrical EngineeringISBN:9780134746968Author:James W. Nilsson, Susan RiedelPublisher:PEARSON
Electric Circuits. (11th Edition)Electrical EngineeringISBN:9780134746968Author:James W. Nilsson, Susan RiedelPublisher:PEARSON Engineering ElectromagneticsElectrical EngineeringISBN:9780078028151Author:Hayt, William H. (william Hart), Jr, BUCK, John A.Publisher:Mcgraw-hill Education,
Engineering ElectromagneticsElectrical EngineeringISBN:9780078028151Author:Hayt, William H. (william Hart), Jr, BUCK, John A.Publisher:Mcgraw-hill Education,





