Chapter 17, Problem 26P

Find the Fourier series representation of the signal shown in Fig. 17.64.

Figure 17.64

To determine

Find the Fourier series representation of the signal shown in Figure 17.64.

Answer to Problem 26P

The Fourier series representation $f\left(t\right)$ of the signal shown in Figure 17.64 is $6+{\displaystyle \sum _{n=1}^{\infty }\left(\begin{array}{l}\left(\frac{15}{2n\pi }\left(-\sin \left(\frac{2n\pi }{5}\right)-\sin \left(\frac{4n\pi }{5}\right)+\sin \left(\frac{6n\pi }{5}\right)+\sin \left(\frac{8n\pi }{5}\right)\right)\right)\cos \left(\frac{2n\pi }{5}\right)t\\ +\left(\frac{15}{2n\pi }\left(\cos \left(\frac{2n\pi }{5}\right)+\cos \left(\frac{4n\pi }{5}\right)-\cos \left(\frac{6n\pi }{5}\right)-\cos \left(\frac{8n\pi }{5}\right)\right)\right)\sin \left(\frac{2n\pi }{5}\right)t\end{array}\right)}$.

Explanation of Solution

Given data:

Refer to Figure 17.64 in the textbook.

Formula used:

Write the expression to calculate the fundamental angular frequency.

${\omega }_0=\frac{2\pi }{T}$ (1)

Here,

$T$ is the period of the function.

Write the general expression to calculate trigonometric Fourier series of $f\left(t\right)$.

$f\left(t\right)=a_0+{\displaystyle \sum _{n=1}^{\infty }\left(a_n\cos n{\omega }_{0}t+b_n\sin n{\omega }_{0}t\right)}$ (2)

Here,

$a_0$ is the dc component of $f\left(t\right)$,

$a_n$ and $b_n$ are the Fourier coefficients,

$n$ is an integer, and

${\omega }_0$ is the angular frequency.

Write the expression to calculate the dc component of the function $f\left(t\right)$.

$a_0=\frac{1}{T}{\displaystyle \underset{0}{\overset{T}{\int }}f\left(t\right)}dt$ (3)

Write the expression to calculate Fourier coefficients.

$a_n=\frac{2}{T}{\displaystyle \underset{0}{\overset{T}{\int }}f\left(t\right)\cos n{\omega }_{0}t}dt$ (4)

$b_n=\frac{2}{T}{\displaystyle \underset{0}{\overset{T}{\int }}f\left(t\right)\sin n{\omega }_{0}t}dt$ (5)

Calculation:

The given waveform is drawn as Figure 1.

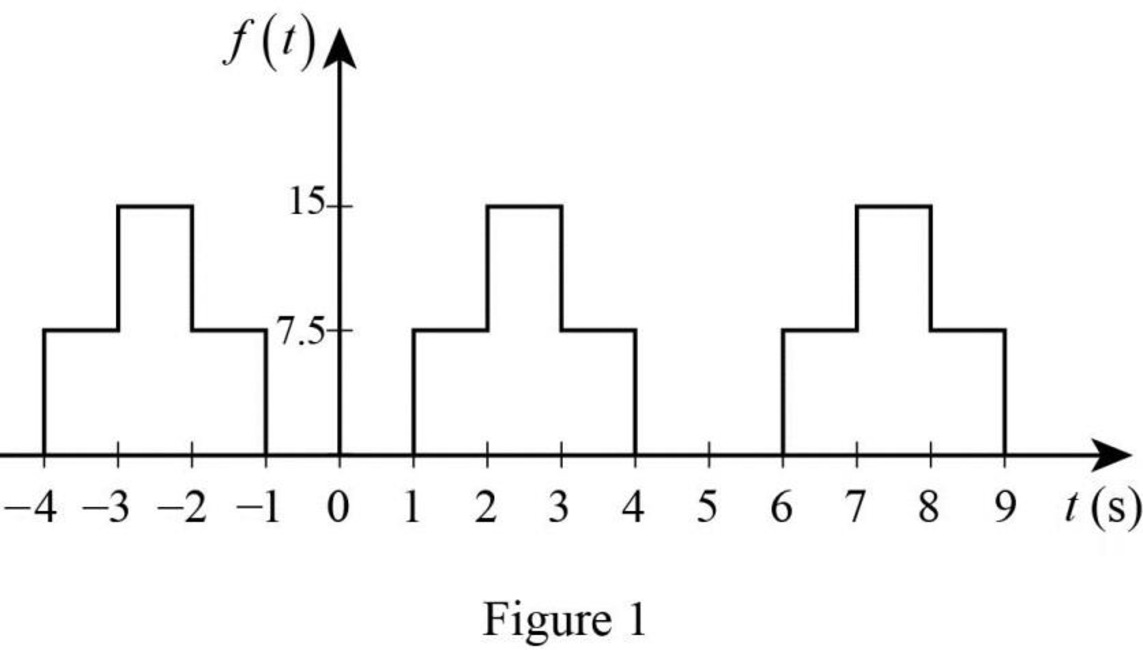
Refer to the Figure 1. The Fourier series function of the waveform is defined as,

$f\left(t\right)=\{\begin{array}{l}0,0<t<1\\ 7.5,1<t<2\\ 15,2<t<3\\ 7.5,3<t<4\\ 0,4<t<5\end{array}$

The time period of the function in Figure 1 is,

$T=5$

Substitute $5$ for $T$ in equation (1) to find ${\omega }_0$.

${\omega }_0=\frac{2\pi }{5}$

Substitute $5$ for $T$ in equation (3) to find $a_0$.

$\begin{array}{c}{a}_0=\frac{1}{5}{\displaystyle \underset{0}{\overset{5}{\int }}f\left(t\right)}dt\\ =\frac{1}{5}\left({\displaystyle \underset{0}{\overset{1}{\int }}f\left(t\right)}dt+{\displaystyle \underset{1}{\overset{2}{\int }}f\left(t\right)}dt+{\displaystyle \underset{2}{\overset{3}{\int }}f\left(t\right)}dt+{\displaystyle \underset{3}{\overset{4}{\int }}f\left(t\right)}dt+{\displaystyle \underset{4}{\overset{5}{\int }}f\left(t\right)}dt\right)\\ =\frac{1}{5}\left({\displaystyle \underset{0}{\overset{1}{\int }}0}dt+{\displaystyle \underset{1}{\overset{2}{\int }}7.5}dt+{\displaystyle \underset{2}{\overset{3}{\int }}15}dt+{\displaystyle \underset{3}{\overset{4}{\int }}7.5}dt+{\displaystyle \underset{4}{\overset{5}{\int }}0}dt\right)\\ =\frac{1}{5}\left(0+{\displaystyle \underset{1}{\overset{2}{\int }}7.5}dt+{\displaystyle \underset{2}{\overset{3}{\int }}15}dt+{\displaystyle \underset{3}{\overset{4}{\int }}7.5}dt+0\right)\end{array}$

Simplify the above equation to find $a_0$.

$\begin{array}{c}{a}_0=\frac{1}{5}\left(7.5{\left[t\right]}_1^2+15{\left[t\right]}_2^3+7.5{\left[t\right]}_3^4\right)\\ =\frac{1}{5}\left(7.5\left[2-1\right]+15\left[3-2\right]+7.5\left[4-3\right]\right)\\ =\frac{1}{5}\left(7.5\left(1\right)+15\left(1\right)+7.5\left(1\right)\right)\\ =6\end{array}$

Substitute $5$ for $T$ and $\frac{2\pi }{5}$ for ${\omega }_0$ in equation (4) to find $a_n$.

$\begin{array}{c}{a}_n=\frac{2}{5}{\displaystyle \underset{0}{\overset{5}{\int }}f\left(t\right)\cos n\left(\frac{2\pi }{5}\right)t}dt\\ =\frac{2}{5}{\displaystyle \underset{0}{\overset{5}{\int }}f\left(t\right)\cos \left(\frac{2n\pi }{5}\right)t}dt\\ =\frac{2}{5}\left(\begin{array}{l}{\displaystyle \underset{0}{\overset{1}{\int }}f\left(t\right)\cos \left(\frac{2n\pi }{5}\right)t}dt+{\displaystyle \underset{1}{\overset{2}{\int }}f\left(t\right)\cos \left(\frac{2n\pi }{5}\right)t}dt\\ +{\displaystyle \underset{2}{\overset{3}{\int }}f\left(t\right)\cos \left(\frac{2n\pi }{5}\right)t}dt+{\displaystyle \underset{3}{\overset{4}{\int }}f\left(t\right)\cos \left(\frac{2n\pi }{5}\right)t}dt\\ +{\displaystyle \underset{4}{\overset{5}{\int }}f\left(t\right)\cos \left(\frac{2n\pi }{5}\right)t}dt\end{array}\right)\\ =\frac{2}{5}\left(\begin{array}{l}{\displaystyle \underset{0}{\overset{1}{\int }}\left(0\right)\cos \left(\frac{2n\pi }{5}\right)t}dt+{\displaystyle \underset{1}{\overset{2}{\int }}7.5\cos \left(\frac{2n\pi }{5}\right)t}dt\\ +{\displaystyle \underset{2}{\overset{3}{\int }}15\cos \left(\frac{2n\pi }{5}\right)t}dt+{\displaystyle \underset{3}{\overset{4}{\int }}7.5\cos \left(\frac{2n\pi }{5}\right)t}dt\\ +{\displaystyle \underset{4}{\overset{5}{\int }}\left(0\right)\cos \left(\frac{2n\pi }{5}\right)t}dt\end{array}\right)\end{array}$

Simplify the above equation to find $a_n$.

$\begin{array}{c}{a}_n=\frac{2}{5}\left(0+{\displaystyle \underset{1}{\overset{2}{\int }}7.5\cos \left(\frac{2n\pi }{5}\right)t}dt+{\displaystyle \underset{2}{\overset{3}{\int }}15\cos \left(\frac{2n\pi }{5}\right)t}dt+{\displaystyle \underset{3}{\overset{4}{\int }}7.5\cos \left(\frac{2n\pi }{5}\right)t}dt+0\right)\\ =\frac{2}{5}\left(7.5{\left[\frac{\sin \left(\frac{2n\pi }{5}\right)t}{\left(\frac{2n\pi }{5}\right)}\right]}_1^2+15{\left[\frac{\sin \left(\frac{2n\pi }{5}\right)t}{\left(\frac{2n\pi }{5}\right)}\right]}_2^3+7.5{\left[\frac{\sin \left(\frac{2n\pi }{5}\right)t}{\left(\frac{2n\pi }{5}\right)}\right]}_3^4\right)\\ =\frac{2}{5}\left(\begin{array}{l}\frac{7.5}{\left(\frac{2n\pi }{5}\right)}\left[\sin \left(\frac{2n\pi }{5}\right)\left(2\right)-\sin \left(\frac{2n\pi }{5}\right)\left(1\right)\right]\\ +\frac{15}{\left(\frac{2n\pi }{5}\right)}\left[\sin \left(\frac{2n\pi }{5}\right)\left(3\right)-\sin \left(\frac{2n\pi }{5}\right)\left(2\right)\right]\\ +\frac{7.5}{\left(\frac{2n\pi }{5}\right)}\left[\sin \left(\frac{2n\pi }{5}\right)\left(4\right)-\sin \left(\frac{2n\pi }{5}\right)\left(3\right)\right]\end{array}\right)\\ =\frac{2}{5}\left(\begin{array}{l}\frac{37.5}{2n\pi }\left[\sin \left(\frac{4n\pi }{5}\right)-\sin \left(\frac{2n\pi }{5}\right)\right]\\ +\frac{75}{2n\pi }\left[\sin \left(\frac{6n\pi }{5}\right)-\sin \left(\frac{4n\pi }{5}\right)\right]\\ +\frac{37.5}{2n\pi }\left[\sin \left(\frac{8n\pi }{5}\right)-\sin \left(\frac{6n\pi }{5}\right)\right]\end{array}\right)\end{array}$

Simplify the above equation to find $a_n$.

$\begin{array}{c}{a}_n=\frac{2}{5}\left(\frac{37.5}{2n\pi }\right)\left(\begin{array}{l}\sin \left(\frac{4n\pi }{5}\right)-\sin \left(\frac{2n\pi }{5}\right)\\ +2\left[\sin \left(\frac{6n\pi }{5}\right)-\sin \left(\frac{4n\pi }{5}\right)\right]\\ +\sin \left(\frac{8n\pi }{5}\right)-\sin \left(\frac{6n\pi }{5}\right)\end{array}\right)\\ =\frac{15}{2n\pi }\left(\begin{array}{l}\sin \left(\frac{4n\pi }{5}\right)-\sin \left(\frac{2n\pi }{5}\right)\\ +2\sin \left(\frac{6n\pi }{5}\right)-2\sin \left(\frac{4n\pi }{5}\right)\\ +\sin \left(\frac{8n\pi }{5}\right)-\sin \left(\frac{6n\pi }{5}\right)\end{array}\right)\\ =\frac{15}{2n\pi }\left(-\sin \left(\frac{2n\pi }{5}\right)-\sin \left(\frac{4n\pi }{5}\right)+\sin \left(\frac{6n\pi }{5}\right)+\sin \left(\frac{8n\pi }{5}\right)\right)\end{array}$

Substitute $5$ for $T$ and $\frac{2\pi }{5}$ for ${\omega }_0$ in equation (5) to find $b_n$.

$\begin{array}{c}{b}_n=\frac{2}{T}{\displaystyle \underset{0}{\overset{T}{\int }}f\left(t\right)\sin n{\omega }_{0}t}dt\\ =\frac{2}{5}{\displaystyle \underset{0}{\overset{5}{\int }}f\left(t\right)\sin \left(\frac{2n\pi }{5}\right)t}dt\\ =\frac{2}{5}\left(\begin{array}{l}{\displaystyle \underset{0}{\overset{1}{\int }}f\left(t\right)\sin \left(\frac{2n\pi }{5}\right)t}dt+{\displaystyle \underset{1}{\overset{2}{\int }}f\left(t\right)\sin \left(\frac{2n\pi }{5}\right)t}dt\\ +{\displaystyle \underset{2}{\overset{3}{\int }}f\left(t\right)\sin \left(\frac{2n\pi }{5}\right)t}dt+{\displaystyle \underset{3}{\overset{4}{\int }}f\left(t\right)\sin \left(\frac{2n\pi }{5}\right)t}dt\\ +{\displaystyle \underset{4}{\overset{5}{\int }}f\left(t\right)\sin \left(\frac{2n\pi }{5}\right)t}dt\end{array}\right)\\ =\frac{2}{5}\left(\begin{array}{l}{\displaystyle \underset{0}{\overset{1}{\int }}\left(0\right)\sin \left(\frac{2n\pi }{5}\right)t}dt+{\displaystyle \underset{1}{\overset{2}{\int }}7.5\sin \left(\frac{2n\pi }{5}\right)t}dt\\ +{\displaystyle \underset{2}{\overset{3}{\int }}15\sin \left(\frac{2n\pi }{5}\right)t}dt+{\displaystyle \underset{3}{\overset{4}{\int }}7.5\sin \left(\frac{2n\pi }{5}\right)t}dt\\ +{\displaystyle \underset{4}{\overset{5}{\int }}\left(0\right)\sin \left(\frac{2n\pi }{5}\right)t}dt\end{array}\right)\end{array}$

Simplify the above equation to find $b_n$.

$\begin{array}{c}{b}_n=\frac{2}{5}\left(0+{\displaystyle \underset{1}{\overset{2}{\int }}7.5\sin \left(\frac{2n\pi }{5}\right)t}dt+{\displaystyle \underset{2}{\overset{3}{\int }}15\sin \left(\frac{2n\pi }{5}\right)t}dt+{\displaystyle \underset{3}{\overset{4}{\int }}7.5\sin \left(\frac{2n\pi }{5}\right)t}dt+0\right)\\ =\frac{2}{5}\left(7.5{\left[-\frac{\cos \left(\frac{2n\pi }{5}\right)t}{\left(\frac{2n\pi }{5}\right)}\right]}_1^2+15{\left[-\frac{\cos \left(\frac{2n\pi }{5}\right)t}{\left(\frac{2n\pi }{5}\right)}\right]}_2^3+7.5{\left[-\frac{\cos \left(\frac{2n\pi }{5}\right)t}{\left(\frac{2n\pi }{5}\right)}\right]}_3^4\right)\\ =\frac{2}{5}\left(\begin{array}{l}-\frac{7.5}{\left(\frac{2n\pi }{5}\right)}\left[\cos \left(\frac{2n\pi }{5}\right)\left(2\right)-\cos \left(\frac{2n\pi }{5}\right)\left(1\right)\right]\\ -\frac{15}{\left(\frac{2n\pi }{5}\right)}\left[\cos \left(\frac{2n\pi }{5}\right)\left(3\right)-\cos \left(\frac{2n\pi }{5}\right)\left(2\right)\right]\\ -\frac{7.5}{\left(\frac{2n\pi }{5}\right)}\left[\cos \left(\frac{2n\pi }{5}\right)\left(4\right)-\cos \left(\frac{2n\pi }{5}\right)\left(3\right)\right]\end{array}\right)\\ =\frac{2}{5}\left(\begin{array}{l}-\frac{37.5}{2n\pi }\left[\cos \left(\frac{4n\pi }{5}\right)-\cos \left(\frac{2n\pi }{5}\right)\right]\\ -\frac{75}{2n\pi }\left[\cos \left(\frac{6n\pi }{5}\right)-\cos \left(\frac{4n\pi }{5}\right)\right]\\ -\frac{37.5}{2n\pi }\left[\cos \left(\frac{8n\pi }{5}\right)-\cos \left(\frac{6n\pi }{5}\right)\right]\end{array}\right)\end{array}$

Simplify the above equation to find $b_n$.

$\begin{array}{c}{b}_n=\frac{2}{5}\left(\frac{37.5}{2n\pi }\right)\left(\begin{array}{l}-\cos \left(\frac{4n\pi }{5}\right)+\cos \left(\frac{2n\pi }{5}\right)\\ -2\left[\cos \left(\frac{6n\pi }{5}\right)-\cos \left(\frac{4n\pi }{5}\right)\right]\\ -\cos \left(\frac{8n\pi }{5}\right)+\cos \left(\frac{6n\pi }{5}\right)\end{array}\right)\\ =\frac{15}{2n\pi }\left(\begin{array}{l}-\cos \left(\frac{4n\pi }{5}\right)+\cos \left(\frac{2n\pi }{5}\right)\\ -2\cos \left(\frac{6n\pi }{5}\right)+2\cos \left(\frac{4n\pi }{5}\right)\\ -\cos \left(\frac{8n\pi }{5}\right)+\cos \left(\frac{6n\pi }{5}\right)\end{array}\right)\\ =\frac{15}{2n\pi }\left(\cos \left(\frac{2n\pi }{5}\right)+\cos \left(\frac{4n\pi }{5}\right)-\cos \left(\frac{6n\pi }{5}\right)-\cos \left(\frac{8n\pi }{5}\right)\right)\end{array}$

Substitute $6$ for $a_0$, $\frac{15}{2n\pi }\left(-\sin \left(\frac{2n\pi }{5}\right)-\sin \left(\frac{4n\pi }{5}\right)+\sin \left(\frac{6n\pi }{5}\right)+\sin \left(\frac{8n\pi }{5}\right)\right)$ for $a_n$, $\frac{15}{2n\pi }\left(\cos \left(\frac{2n\pi }{5}\right)+\cos \left(\frac{4n\pi }{5}\right)-\cos \left(\frac{6n\pi }{5}\right)-\cos \left(\frac{8n\pi }{5}\right)\right)$ for $b_n$, and $\frac{2\pi }{5}$ for ${\omega }_0$ in equation (2) to find $f\left(t\right)$.

$\begin{array}{c}f\left(t\right)=6+{\displaystyle \sum _{n=1}^{\infty }\left(\begin{array}{l}\left(\frac{15}{2n\pi }\left(-\sin \left(\frac{2n\pi }{5}\right)-\sin \left(\frac{4n\pi }{5}\right)+\sin \left(\frac{6n\pi }{5}\right)+\sin \left(\frac{8n\pi }{5}\right)\right)\right)\cos n\left(\frac{2\pi }{5}\right)t\\ +\left(\frac{15}{2n\pi }\left(\cos \left(\frac{2n\pi }{5}\right)+\cos \left(\frac{4n\pi }{5}\right)-\cos \left(\frac{6n\pi }{5}\right)-\cos \left(\frac{8n\pi }{5}\right)\right)\right)\sin n\left(\frac{2\pi }{5}\right)t\end{array}\right)}\\ =6+{\displaystyle \sum _{n=1}^{\infty }\left(\begin{array}{l}\left(\frac{15}{2n\pi }\left(-\sin \left(\frac{2n\pi }{5}\right)-\sin \left(\frac{4n\pi }{5}\right)+\sin \left(\frac{6n\pi }{5}\right)+\sin \left(\frac{8n\pi }{5}\right)\right)\right)\cos \left(\frac{2n\pi }{5}\right)t\\ +\left(\frac{15}{2n\pi }\left(\cos \left(\frac{2n\pi }{5}\right)+\cos \left(\frac{4n\pi }{5}\right)-\cos \left(\frac{6n\pi }{5}\right)-\cos \left(\frac{8n\pi }{5}\right)\right)\right)\sin \left(\frac{2n\pi }{5}\right)t\end{array}\right)}\end{array}$

Conclusion:

Thus, the Fourier series representation $f\left(t\right)$ of the signal shown in Figure 17.64 is $6+{\displaystyle \sum _{n=1}^{\infty }\left(\begin{array}{l}\left(\frac{15}{2n\pi }\left(-\sin \left(\frac{2n\pi }{5}\right)-\sin \left(\frac{4n\pi }{5}\right)+\sin \left(\frac{6n\pi }{5}\right)+\sin \left(\frac{8n\pi }{5}\right)\right)\right)\cos \left(\frac{2n\pi }{5}\right)t\\ +\left(\frac{15}{2n\pi }\left(\cos \left(\frac{2n\pi }{5}\right)+\cos \left(\frac{4n\pi }{5}\right)-\cos \left(\frac{6n\pi }{5}\right)-\cos \left(\frac{8n\pi }{5}\right)\right)\right)\sin \left(\frac{2n\pi }{5}\right)t\end{array}\right)}$.