
Concept explainers
For a rigid body in plane motion, show that the system of the inertial terms consists of
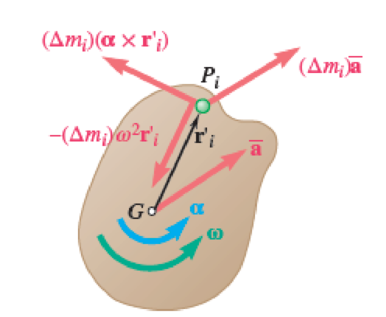
Fig. P16.47
Want to see the full answer?
Check out a sample textbook solution
Chapter 16 Solutions
VEC MECH 180-DAT EBOOK ACCESS(STAT+DYNA)
Additional Engineering Textbook Solutions
Engineering Mechanics: Statics
HEAT+MASS TRANSFER:FUND.+APPL.
DeGarmo's Materials and Processes in Manufacturing
Engineering Mechanics: Statics & Dynamics (14th Edition)
Applied Statics and Strength of Materials (6th Edition)
Vector Mechanics For Engineers
- 1. Determine the kinetic energy of the system of Fig.3.16 at an arbitrary instant in terms of x, including the inertia effects of the springs. 2m ima k. m, No slip 81, E k, m, F77777arrow_forwardFor the system given, the bar AB has an angular velocity of wAB=4 rad/s. By use of vector notation, determine the velocity of mass C, and the angular velocity of bar BC when Ɵ=30°.arrow_forwardGiven that P = 50N, and the rod has mass = 0.370 kg with centroidal mass moment of inertia l = 37/19200 kg-m²:a. Which of the equations given in the second image can be used to solve for the angular acceleration of rod BD?b. What is the angular acceleration of rod BD?arrow_forward
- A shaft carries four masses A, B, C and D of magnitudes 18 kg, 15 kg, 27 kg, and 22.5 kg respectively and revolving at radii 20 mm, 25 mm, 30 mm and 15 mm respectively. The masses are rotating in the same plane. The angular position of masses B, C and D are 60 degrees , 135 degrees and 270 degrees from mass A. Find the magnitude and position of the balancing mass at a radius of 50 mm,arrow_forwardA ring of mass m =1 kg and radius R = 1m is attached to a vertical shaft by means of a frictionless pin. Coordinates xyz are fixed to the ring as shown and the frictionless pin at A is aligned with the x-axis. The vertical shaft precesses about the Z-axis with constant angular velocity 2 = 1 rad/s. (a) At a particular moment when 0 = 30° and = 4 rad/s, find the value of Ö . This comes from a sum of the moments about the x-axis. Do not neglect gravity. (b) Find the torque or moment necessary that must be applied about the vertical shaft in order to keep it turning at a constant rate of N = 1 rad/s. Ring R XG A 1 Ixx = lyy =mR? G Iz = mR?arrow_forwardR - m 130° A hollow wheel of mass given by m 50 kg rolls down an incline of 30° without slipping. The inner radius of the wheel is given by R = 50 mm and its thickness is given by d = 5 mm. Gravity acts down. (a) Show that the moment of inertia of the wheel is given by Ī = 138 125 kg mm². (b) Show that the linear acceleration of the wheel's centre of gravity ā is related to the angular acceleration of the wheel a via a (55 mm)a. = (c) Analyse an appropriate free-body diagram to determine the linear acceleration of the wheel's centre of gravity ā.arrow_forward
- A conservative mechanical system consists of a mass m that is constrained to move along a circle of radius R. The centre of the circle is at the origin O of the coordinate system. The mass is connected to a point A along the â-axis at a distance 2R from the centre of circle with a spring of elastic constant k, so that the corresponding elastic potential has the form Vspring = (k/2)ď², where d is the (varying) distance between the mass and point A. Gravity acts, as usual, along the vertical direction. See the figure for a depiction of the system. 0 m (b) Write down the Lagrangian of the system. (a) How many degrees of freedom does the system have? Indicate generalised coordinates to describe the motion of the system. X (c) Write down the corresponding Euler-Lagrange equation(s).arrow_forwardA rotating shaft carries four unbalanced masses 20 kg, 16 kg, 18 kg and 14 kg at radii 55 mm, 65 mm, 75 mm and 65 mm respectively. The 2nd, 3rd and 4th masses revolve in planes 80 mm, 160 mm and 280 mm respectively measured from the plane of the first mass and are angularly located at 65°, 135° and 270° respectively measured clockwise from the first mass.The shaft is dynamically balanced by two masses, both located at 55 mm radii and revolving in planes mid-way between those of 1st and 2nd masses and midway between those of 3rd and 4th masses. Determine, balancing mass by drawing couple polygon and their respective angular position graphically.arrow_forwardA drum can rotate about a fixed-point O. The A block is attached to a cord wrapping around the drum. The mass of the drum is md = 100kg and the radius is r = 0.5 m. The radius of gyration of the drum about point O is ko=0.3 m. The mass of the block is mb= 20kg. The block is released from rest. The acceleration due to gravity is g=9.81 m/s2. (3) Calculate the angular acceleration of the drum α= ________ (rad/s2) (two decimal places)arrow_forward
- A drum can rotate about a fixed-point O. The A block is attached to a cord wrapping around the drum. The mass of the drum is md = 100kg and the radius is r = 0.5 m. The radius of gyration of the drum about point O is ko=0.3 m. The mass of the block is mb= 20kg. The block is released from rest. The acceleration due to gravity is g=9.81 m/s2. (1) Calculate the mass moment of inertia of the drum about the point O, IO_______(kgm2) (two decimal places)arrow_forwardA drum can rotate about a fixed-point O. The A block is attached to a cord wrapping around the drum. The mass of the drum is md = 100kg and the radius is r = 0.5 m. The radius of gyration of the drum about point O is ko=0.3 m. The mass of the block is mb= 20kg. The block is released from rest. The acceleration due to gravity is g=9.81 m/s2. (1) Calculate the mass moment of inertia of the drum about the point O, IO_______(kgm2) (two decimal places)arrow_forwardA drum can rotate about a fixed-point O. The A block is attached to a cord wrapping around the drum. The mass of the drum is md = 100kg and the radius is r = 0.5 m. The radius of gyration of the drum about point O is ko=0.3 m. The mass of the block is mb= 20kg. The block is released from rest. The acceleration due to gravity is g=9.81 m/s2. (3) Calculate the angular acceleration of the drum α= ________ (rad/s2) (two decimal places)arrow_forward
 Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY





