VEC MECH 180-DAT EBOOK ACCESS(STAT+DYNA)
12th Edition
ISBN: 9781260916942
Author: BEER
Publisher: MCG
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 16, Problem 16.155RP
The total mass of the Baja car and driver, including the wheels, is 250 kg. Each pair of 58-cm radius wheels and the axle has a total mass of 20 kg and a mass moment of inertia of 2.9 kg·m2. The center of gravity of the driver and Baja body (not including the wheels) is located x = 0.70 m from the rear axle A and y = 0.55 m from the ground. The wheelbase is L = 1.60 m. If the engine exerts a torque of 500 N·m on the rear axle, what is the car’s acceleration?
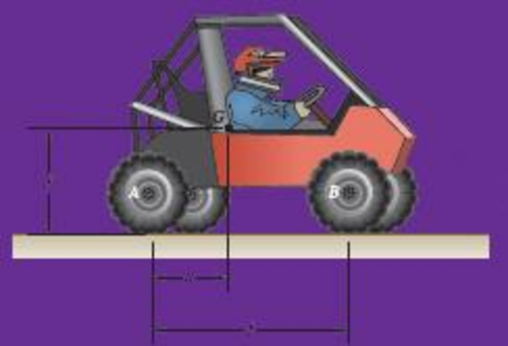
Fig. P16.155
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Locate mass A at 35 mm from support X.Locate mass B at 96.5 mm from support X. Locate mass C at 122.7 mm from support X.Position mass A at zero degrees and D at 90o from A.
A
B
C
D
mass(kg)
0.021
0.044
0.059
0.019
essentric length(r) m
0.036
0.025
0.034
0.036
6.1. Use the graphical method to determine the angular position of masses B and C.6.2. Calculate the position of mass D from support X.6.3. If the shaft rotates at 150 r.p.m calculate the dynamic force experienced by the bearings.
The drum shown in Fig. (a) has a radius of gyration of 30 cm
and weights 1,8 kN. It is supported by means of small hubs
which rest in bearings. A weight of 1 kN is attached to one end
of a rope, the other end being wrapped around the drum.
Neglecting friction in the bearings, determine the acceleration
of the weight, the angular acceleration of the drum, and the
tension in the rope.
37.5 cm
1.8kN
T
IkN
The body and bucket of a skid steer loader has a
weight of 1990 lb, and its center of gravity is located at
G. Each of the four wheels has a weight of 95 lb and a
radius of gyration about its center of gravity of 1 ft.(
Figure 1)
Figure
1.25 ft
G1.25 ft
2 ft 1 ft
Part A
If the engine supplies a torque of M = 90 lb-ft to each of the rear drive wheels, determine the speed of the loader in t = 10 s
starting from rest. The wheels roll without slipping.
Express your answer with the appropriate units.
v=
Value
Submit
μA
Provide Feedback
Request Answer
Units
Review
?
Next >
Chapter 16 Solutions
VEC MECH 180-DAT EBOOK ACCESS(STAT+DYNA)
Ch. 16.1 - Two pendulums, A and B, with the masses and...Ch. 16.1 - Two pendulums, A and B, with the masses and...Ch. 16.1 - Two solid cylinders, A and B, have the same mass m...Ch. 16.1 - Prob. 16.1FBPCh. 16.1 - Prob. 16.2FBPCh. 16.1 - Prob. 16.3FBPCh. 16.1 - The 400-lb crate shown is lowered by means of two...Ch. 16.1 - A 60-lb uniform thin panel is placed in a truck...Ch. 16.1 - A 60-lb uniform thin panel is placed in a truck...Ch. 16.1 - A loading car is at rest on a track forming an...
Ch. 16.1 - A 2100-lb rear-wheel-drive tractor carries a 900...Ch. 16.1 - A uniform rod BC of mass 4 kg is connected to a...Ch. 16.1 - A 2000-kg truck is being used to lift a 400-kg...Ch. 16.1 - The support bracket shown is used to transport a...Ch. 16.1 - Prob. 16.8PCh. 16.1 - A 20-kg cabinet is mounted on casters that allow...Ch. 16.1 - Solve Prob. 16.9, assuming that the casters are...Ch. 16.1 - Prob. 16.11PCh. 16.1 - Prob. 16.12PCh. 16.1 - The retractable shelf shown is supported by two...Ch. 16.1 - Bars AB and BE, each with a mass of 4 kg, are...Ch. 16.1 - At the instant shown, the tensions in the vertical...Ch. 16.1 - Three bars, each of mass 3 kg, are welded together...Ch. 16.1 - Members ACE and DCB are each 600 mm long and are...Ch. 16.1 - A prototype rotating bicycle rack is designed to...Ch. 16.1 - The control rod AC is guided by two pins that...Ch. 16.1 - The coefficients of friction between the 30-lb...Ch. 16.1 - Prob. 16.21PCh. 16.1 - Prob. 16.22PCh. 16.1 - For a rigid body in translation, show that the...Ch. 16.1 - For a rigid body in centroidal rotation, show that...Ch. 16.1 - It takes 10 min for a 2.4-Mg flywheel to coast to...Ch. 16.1 - The rotor of an electric motor has an angular...Ch. 16.1 - The 10-in.-radius brake drum is attached to a...Ch. 16.1 - The 10-in.-radius brake drum is attached to a...Ch. 16.1 - The 100-mm-radius brake drum is attached to a...Ch. 16.1 - The 180-mm-radius disk is at rest when it is...Ch. 16.1 - Solve Prob. 16.30, assuming that the direction of...Ch. 16.1 - In order to determine the mass moment of inertia...Ch. 16.1 - The flywheel shown has a radius of 20 in., a...Ch. 16.1 - Each of the double pulleys shown has a mass moment...Ch. 16.1 - Two disks A and B, of mass mA = 2 kg and mB = 4...Ch. 16.1 - Two disks A and B, of mass mA = 2 kg and mB = 4...Ch. 16.1 - Gear A weighs 1 lb and has a radius of gyration of...Ch. 16.1 - The 25-lb double pulley shown is at rest and in...Ch. 16.1 - A belt of negligible mass passes between cylinders...Ch. 16.1 - Prob. 16.40PCh. 16.1 - Disk A has a mass of 6 kg and an initial angular...Ch. 16.1 - Prob. 16.42PCh. 16.1 - Disk A has a mass mA = 4 kg, a radius rA = 300 mm,...Ch. 16.1 - Disk B is at rest when it is brought into contact...Ch. 16.1 - Prob. 16.45PCh. 16.1 - Prob. 16.46PCh. 16.1 - For a rigid body in plane motion, show that the...Ch. 16.1 - A uniform slender rod AB rests on a frictionless...Ch. 16.1 - Prob. 16.49PCh. 16.1 - Prob. 16.50PCh. 16.1 - Prob. 16.51PCh. 16.1 - A 250-lb satellite has a radius of gyration of 24...Ch. 16.1 - A rectangular plate of mass 5 kg is suspended from...Ch. 16.1 - Prob. 16.54PCh. 16.1 - A drum with a 200-mm radius is attached to a disk...Ch. 16.1 - A drum with a 200-mm radius is attached to a disk...Ch. 16.1 - The 12-lb uniform disk shown has a radius of r =...Ch. 16.1 - Prob. 16.58PCh. 16.1 - Prob. 16.59PCh. 16.1 - 16.60 and 16.61The 400-lb crate shown is lowered...Ch. 16.1 - Prob. 16.61PCh. 16.1 - Two uniform cylinders, each of weight W = 14 lb...Ch. 16.1 - Prob. 16.63PCh. 16.1 - Prob. 16.64PCh. 16.1 - A uniform slender bar AB with a mass m is...Ch. 16.1 - Prob. 16.66PCh. 16.1 - 16.66 through 16.68A thin plate of the shape...Ch. 16.1 - 16.66 through 16.68A thin plate of the shape...Ch. 16.1 - A sphere of radius r and mass m is projected along...Ch. 16.1 - Solve Prob. 16.69, assuming that the sphere is...Ch. 16.1 - A bowler projects an 8-in.-diameter ball weighing...Ch. 16.1 - Prob. 16.72PCh. 16.1 - A uniform sphere of radius r and mass m is placed...Ch. 16.1 - A sphere of radius r and mass m has a linear...Ch. 16.2 - A cord is attached to a spool when a force P is...Ch. 16.2 - Prob. 16.5CQCh. 16.2 - Prob. 16.6CQCh. 16.2 - Prob. 16.7CQCh. 16.2 - Prob. 16.5FBPCh. 16.2 - Two identical 4-lb slender rods AB and BC are...Ch. 16.2 - Prob. 16.7FBPCh. 16.2 - Prob. 16.8FBPCh. 16.2 - Show that the couple I of Fig. 16.15 can be...Ch. 16.2 - A uniform slender rod of length L = 900 mm and...Ch. 16.2 - A crate of mass 80 kg is held in the position...Ch. 16.2 - A uniform slender rod of length L = 36 in. and...Ch. 16.2 - In Prob. 16.78, determine (a) the distance h for...Ch. 16.2 - An athlete performs a leg extension on a machine...Ch. 16.2 - Prob. 16.81PCh. 16.2 - A turbine disk weighing 50 lb rotates at a...Ch. 16.2 - The 80-lb tailgate of a car is supported by the...Ch. 16.2 - A uniform rod of length L and mass m is supported...Ch. 16.2 - Three stage lights are mounted on a pipe fixture...Ch. 16.2 - An adapted launcher uses a torsional spring about...Ch. 16.2 - A 4-kg slender rod is welded to the edge of a 3-kg...Ch. 16.2 - Prob. 16.88PCh. 16.2 - The object ABC consists of two slender rods welded...Ch. 16.2 - A 3.5-kg slender rod AB and a 2-kg slender rod BC...Ch. 16.2 - A 9-kg uniform disk is attached to the 5-kg...Ch. 16.2 - Derive the equation MC=IC for the rolling disk of...Ch. 16.2 - Prob. 16.93PCh. 16.2 - Prob. 16.94PCh. 16.2 - Prob. 16.95PCh. 16.2 - Prob. 16.96PCh. 16.2 - A 40-kg flywheel of radius R = 0.5 m is rigidly...Ch. 16.2 - Prob. 16.98PCh. 16.2 - 16.98 through 16.101A drum of 80-mm radius is...Ch. 16.2 - 16.98 through 16.101A drum of 80-mm radius is...Ch. 16.2 - 16.98 through 16.101A drum of 80-mm radius is...Ch. 16.2 - 16.102 through 16.105A drum of 4-in. radius is...Ch. 16.2 - 16.102 through 16.105A drum of 4-in. radius is...Ch. 16.2 - 16.102 through 16.105A drum of 4-in. radius is...Ch. 16.2 - 16.102 through 16.105A drum of 4-in. radius is...Ch. 16.2 - 16.106 and 16.107A 12-in.-radius cylinder of...Ch. 16.2 - 16.106 and 16.107A 12-in.-radius cylinder of...Ch. 16.2 - Gear C has a mass of 5 kg and a centroidal radius...Ch. 16.2 - Two uniform disks A and B, each with a mass of 2...Ch. 16.2 - A single-axis personal transport device starts...Ch. 16.2 - A hemisphere of weight W and radius r is released...Ch. 16.2 - A hemisphere of weight W and radius r is released...Ch. 16.2 - The center of gravity G of a 1.5-kg unbalanced...Ch. 16.2 - A small clamp of mass mB is attached at B to a...Ch. 16.2 - Prob. 16.115PCh. 16.2 - A 4-lb bar is attached to a 10-lb uniform cylinder...Ch. 16.2 - The uniform rod AB with a mass m and a length of...Ch. 16.2 - Prob. 16.118PCh. 16.2 - Prob. 16.119PCh. 16.2 - Prob. 16.120PCh. 16.2 - End A of the 6-kg uniform rod AB rests on the...Ch. 16.2 - End A of the 6-kg uniform rod AB rests on the...Ch. 16.2 - End A of the 8-kg uniform rod AB is attached to a...Ch. 16.2 - The 4-kg uniform rod ABD is attached to the crank...Ch. 16.2 - The 3-lb uniform rod BD is connected to crank AB...Ch. 16.2 - The 3-lb uniform rod BD is connected to crank AB...Ch. 16.2 - The test rig shown was developed to perform...Ch. 16.2 - Solve Prob. 16.127 for = 90. 16.127The test rig...Ch. 16.2 - The 4-kg uniform slender bar BD is attached to bar...Ch. 16.2 - The motion of the uniform slender rod of length L...Ch. 16.2 - At the instant shown, the 20-ft-long, uniform...Ch. 16.2 - A driver starts his car with the door on the...Ch. 16.2 - Prob. 16.133PCh. 16.2 - The hatchback of a car is positioned as shown to...Ch. 16.2 - The 6-kg rod BC connects a 10-kg disk centered at...Ch. 16.2 - Prob. 16.136PCh. 16.2 - In the engine system shown, l = 250 mm and b = 100...Ch. 16.2 - Solve Prob. 16.137 when = 90. 16.137In the engine...Ch. 16.2 - The 4-lb uniform slender rod AB, the 8-lb uniform...Ch. 16.2 - The 4-lb uniform slender rod AB, the 8-lb uniform...Ch. 16.2 - Two rotating rods in the vertical plane are...Ch. 16.2 - Two rotating rods in the vertical plane are...Ch. 16.2 - Two disks, each with a mass m and a radius r, are...Ch. 16.2 - A uniform slender bar AB of mass m is suspended as...Ch. 16.2 - A uniform rod AB, of mass 15 kg and length 1 m, is...Ch. 16.2 - The uniform slender 2-kg bar BD is attached to the...Ch. 16.2 - Prob. 16.147PCh. 16.2 - Prob. 16.148PCh. 16.2 - Prob. 16.149PCh. 16.2 - Prob. 16.150PCh. 16.2 - (a) Determine the magnitude and the location of...Ch. 16.2 - Prob. 16.152PCh. 16 - A cyclist is riding a bicycle at a speed of 20 mph...Ch. 16 - The forklift truck shown weighs 3200 lb and is...Ch. 16 - The total mass of the Baja car and driver,...Ch. 16 - Identical cylinders of mass m and radius r are...Ch. 16 - Prob. 16.157RPCh. 16 - The uniform rod AB of weight W is released from...Ch. 16 - Prob. 16.159RPCh. 16 - Prob. 16.160RPCh. 16 - A cylinder with a circular hole is rolling without...Ch. 16 - Two 3-kg uniform bars are connected to form the...Ch. 16 - A crate of mass 80 kg is held in the position...Ch. 16 - The Geneva mechanism shown is used to provide an...
Additional Engineering Textbook Solutions
Find more solutions based on key concepts
Compute the hydraulic radius for a circular drain pipe running half full if its inside diameter is 300 mm.
Applied Fluid Mechanics (7th Edition)
What types of polymers are most commonly blow molded?
Degarmo's Materials And Processes In Manufacturing
What types of coolant are used in vehicles?
Automotive Technology: Principles, Diagnosis, and Service (5th Edition)
Steady state conduction rate to the warm compressor to the net power produces theoretically by thermodynamic ba...
Introduction to Heat Transfer
The moment of inertia Iy for the slender rod in terms of the rod’s total mass m .
Engineering Mechanics: Statics & Dynamics (14th Edition)
The spring of k and unstretched length 1.5R is attached to the disk at a radial distance of 0.75R from the cent...
Engineering Mechanics: Statics
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, mechanical-engineering and related others by exploring similar questions and additional content below.Similar questions
- A yoyo is constructed by attaching three uniform, solid disks along their central axes as shown. The two outer disks are identical, each with mass M = 58 g, radius R = 3.3 cm, and moment of inertia 1/2MR2. The central, smaller disk has mass M/2 and radius R/2. A light, flexible string of negligible mass is wrapped counterclockwise around the central disk of the yoyo. The yoyo is then placed on a horizontal tabletop and the string is gently pulled with a constant force F = 0.25 N. The tension in the string is not sufficient to cause the yoyo to leave the tabletop. In this problem consider the two cases show. In Case 1 the string is pulled straight up, perpendicular to the tabletop. In Case 2 the string is pulled horizontally, parallel to the tabletop. In both cases the yoyo rolls without slipping. In both the cases shown what is the magnitude of the tourqe t excerted by the string about the contact point of the yo-yo wiith the table in N*m. What is the moment of intertia of the yo-yo…arrow_forwardConsider a wheel with four spokes as shown below. The radius of wheel is r = 0.18 m. The mass of the circumferential part is 0.7 kg, and the mass of each spoke is 0.12 kg. If one of the spokes is removed, calculate the distance (in mm) between the old and new center of mass locations. rarrow_forwardThe 10-kg door shown is 80 cm by 120 cm and has a constant thickness before the circular cut (diameter = 15 cm) is made. Calculate the centroid and mass moment of inertia about the z-axis (through the origin) of the door with the hole cut. $15cm gy ૧º- ↓ 80cm 120cmarrow_forward
- it is known that the shaft in the shape with a rotating disk on it rotates parallel to the horizontal plane. rotation speeds are wr=955 wp=296 rpm. Find the mass of the rotating disk to remain in a parallel position.gravitational acceleration g=9.81 m 2. mass moment of inertia of disk I=0.090479 kgm 2arrow_forwardConsider the system of two blocks. Thereis no friction between block A and the tabletop. The mass of block B is5.00 kg. The pulley rotates about a frictionless axle, and the light ropedoesn’t slip on the pulley surface. The pulley has radius 0.200 m andmoment of inertia 1.30 kg . m2. If the pulley is rotating with an angularspeed of 8.00 rad/s after the block has descended 1.20 m, what is themass of block A?arrow_forwardThe figure at right shows a child’s toy. This toy takes the form of a cylinder mounted on top of a hemisphere, of total mass M. The radius of the hemisphere is R, and the CM of the toy is a height h above the floor when the toy is vertical. Assume that the cylinder and the hemisphere have the same density. In terms of R, what is the maximumthickness d of the cylinder for which the toy will remain stable?arrow_forward
- A shaft with 3 meters span between two bearings carries two masses of 120 g and 100 g acting at the extremities of the arms 40 mm and 50 mm long respectively. The planes in which these masses rotate are 1.5 m and 2.5 m respectively from the left end bearing supporting the shaft. The angle between the arms is 120°. The speed of rotation of the shaft is 200 r.p.m. If the masses are balanced by two counter-masses rotating with the shaft acting at radii of 0.3 m and placed at 0.5 m from each bearing centers, estimate the magnitude of the two balance masses and their orientation with respect to the X-axis, i.e. mass of 120 g.arrow_forwardA shaft with 3 meters span between two bearings carries two masses of 10 kg and 20 kg acting at the extremities of the arms 0.45 m and 0.6 m long respectively. The planes in which these masses rotate are 1.2 m and 2.4 m respectively from the left end bearing supporting the shaft. The angle between the arms is 60°. The speed of rotation of the shaft is 200 r.p.m. If the masses are balanced by two counter-masses rotating with the shaft acting at radii of 0.3 m and placed at 0.3 m from each bearing centers, estimate the magnitude of the two balance masses and their orientation with respect to the X-axis, i.e. mass of 10 kg.arrow_forwardA shaft with 3 meters span between two bearings carries two masses of 10 kg and 20 kg acting at the extremities of the arms 0.45 m and 0.6 m long respectively. The planes in which these masses rotate are 1.2 m and 2.4 m respectively from the left end bearing supporting the shaft. The angle between the arms is 60°. The speed of rotation of the shaft is 200 r.p.m. If the masses are balanced by two counter-masses rotating with the shaft acting at radii of 0.3 m and placed at 0.3 m from each bearing centers, estimate the magnitude of the two balance masses and their orientation with respect to the X-axis, i.e. mass of 10 kg Note: It must be solved using the graphic method, not the equations method.arrow_forward
- Please solve accurate and fast answer thanksarrow_forwardThree bodies are fixed on a shaft rotating at 500 rpm. The mass of the bodies are 3.5 kg, 2.5 kg and 2 kg. The radii of rotation can be taken as 60 cm, 40 cm and 25 cm. If a balancing body of 1.5 kg is to be placed, then find the unbalance in the system. The first body can be assumed to be at 45° from positive x axis, second body is at 90° from first body and third body is at 180° from positive x-axis. All the angles are measured in anti-clockwise direction.arrow_forwardA window cleaner is pulling himself up to a pulley that consists of two disks welded together as shown. The person is currently pulling straight down on the rope in his hands with a force of magnitude 580.4 N. The other rope is also vertical and is attached to the person's center of mass. The person's mass is 74.2 kg, the pulley's total moment of inertia is 395 kgm2, the radius of the small disk is 0.39 m, and the radius of the big disk is 0.73 m.What is the magnitude of the acceleration of the person's center of mass?arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Elements Of Electromagnetics
Mechanical Engineering
ISBN:9780190698614
Author:Sadiku, Matthew N. O.
Publisher:Oxford University Press
Mechanics of Materials (10th Edition)
Mechanical Engineering
ISBN:9780134319650
Author:Russell C. Hibbeler
Publisher:PEARSON
Thermodynamics: An Engineering Approach
Mechanical Engineering
ISBN:9781259822674
Author:Yunus A. Cengel Dr., Michael A. Boles
Publisher:McGraw-Hill Education
Control Systems Engineering
Mechanical Engineering
ISBN:9781118170519
Author:Norman S. Nise
Publisher:WILEY
Mechanics of Materials (MindTap Course List)
Mechanical Engineering
ISBN:9781337093347
Author:Barry J. Goodno, James M. Gere
Publisher:Cengage Learning
Engineering Mechanics: Statics
Mechanical Engineering
ISBN:9781118807330
Author:James L. Meriam, L. G. Kraige, J. N. Bolton
Publisher:WILEY
Dynamics - Lesson 1: Introduction and Constant Acceleration Equations; Author: Jeff Hanson;https://www.youtube.com/watch?v=7aMiZ3b0Ieg;License: Standard YouTube License, CC-BY