Chapter 16, Problem 28P

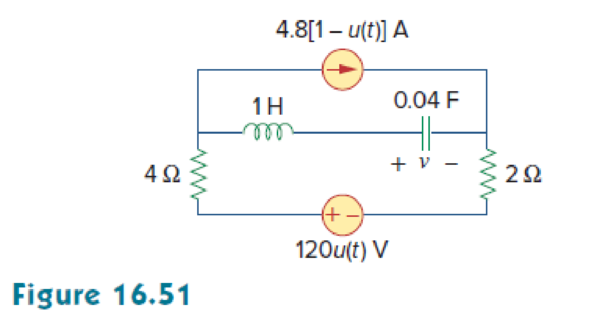
For the circuit in Fig. 16.51, find v(t) for t > 0.

To determine

Find the expression of voltage $v\left(t\right)$ for $t>0$ in the circuit of Figure 16.51.

Answer to Problem 28P

The expression of voltage $v\left(t\right)$ for $t>0$ in the circuit of Figure 16.51 is $\left[120+186e^{-3t}\cos \left(4t+143.13°\right)\right]u\left(t\right)\text{V}$.

Explanation of Solution

Given data:

Refer to Figure 16.51 in the textbook.

Formula used:

Write an expression to calculate the value of step input.

$u\left(t\right)=\{\begin{array}{l}0t<0\\ 1t>0\end{array}$

Write a general expression to calculate the impedance of a resistor in s-domain.

$Z_R=R$ (1)

Here,

$R$ is the value of resistance.

Write a general expression to calculate the impedance of an inductor in s-domain.

$Z_L=sL$ (2)

Here,

$L$ is the value of inductance.

Write a general expression to calculate the impedance of a capacitor in s-domain.

$Z_C=\frac{1}{sC}$ (3)

Here,

$C$ is the value of capacitance.

Calculation:

The given circuit is redrawn as shown in Figure 1.

For a DC circuit, at steady state condition when time $t=0^{-}$ the capacitor acts like open circuit and the inductor acts like short circuit.

The value of current source is calculated as follows:

$\begin{array}{c}{i}_s\left(t\right)=4.8\left(1-0\right)\left\{\because u\left(t\right)=0\text{for}t<0\right\}\\ =4.8\text{A}\end{array}$

The value of voltage source is calculated as follows:

$\begin{array}{c}{v}_s\left(t\right)=120\left(0\right)\text{V}\left\{\because u\left(t\right)=0\text{for}t<0\right\}\\ =\text{0}\text{V}\end{array}$

Since the value of voltage source is zero it is short circuited.

Now, the Figure 1 is reduced as shown in Figure 2.

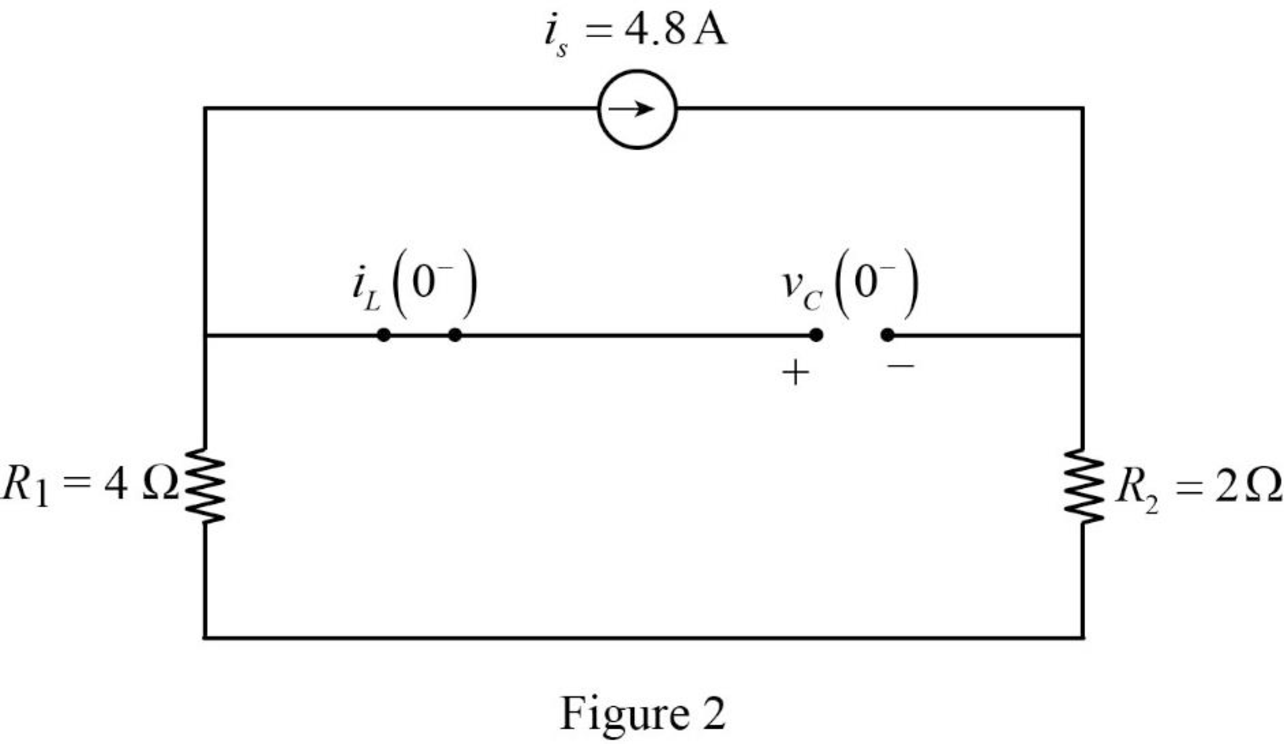
Refer to Figure 2, the capacitor is connected in parallel with the series connected resistors $R_1$ and $R_2$. The voltage across the capacitor is calculated as follows:

$\begin{array}{c}{v}_C\left(0^{-}\right)=\left(-4.8\text{A}\right)\left(4\Omega +2\Omega \right)\\ =-28.8\text{V}\end{array}$

Refer to Figure 2, since the capacitor is open circuited there is no current flow through the inductor.

$i_L\left(0^{-}\right)=0\text{A}$

The current through inductor and voltage across capacitor is always continuous so that,

$i\left(0\right)=i_L\left(0^{-}\right)=i_L\left(0^{+}\right)=0\text{A}$

$v\left(0\right)=v_C\left(0^{-}\right)=v_C\left(0^{+}\right)=-28.8\text{V}$

For time $t>0$:

The value of current source is calculated as follows:

$\begin{array}{c}{i}_s\left(t\right)=4.8\left(1-1\right)\left\{\because u\left(t\right)=1\text{for}t>0\right\}\\ =0\text{A}\end{array}$

Since the value of current source is zero it is open circuited.

Now, the Figure 1 is reduced as shown in Figure 3.

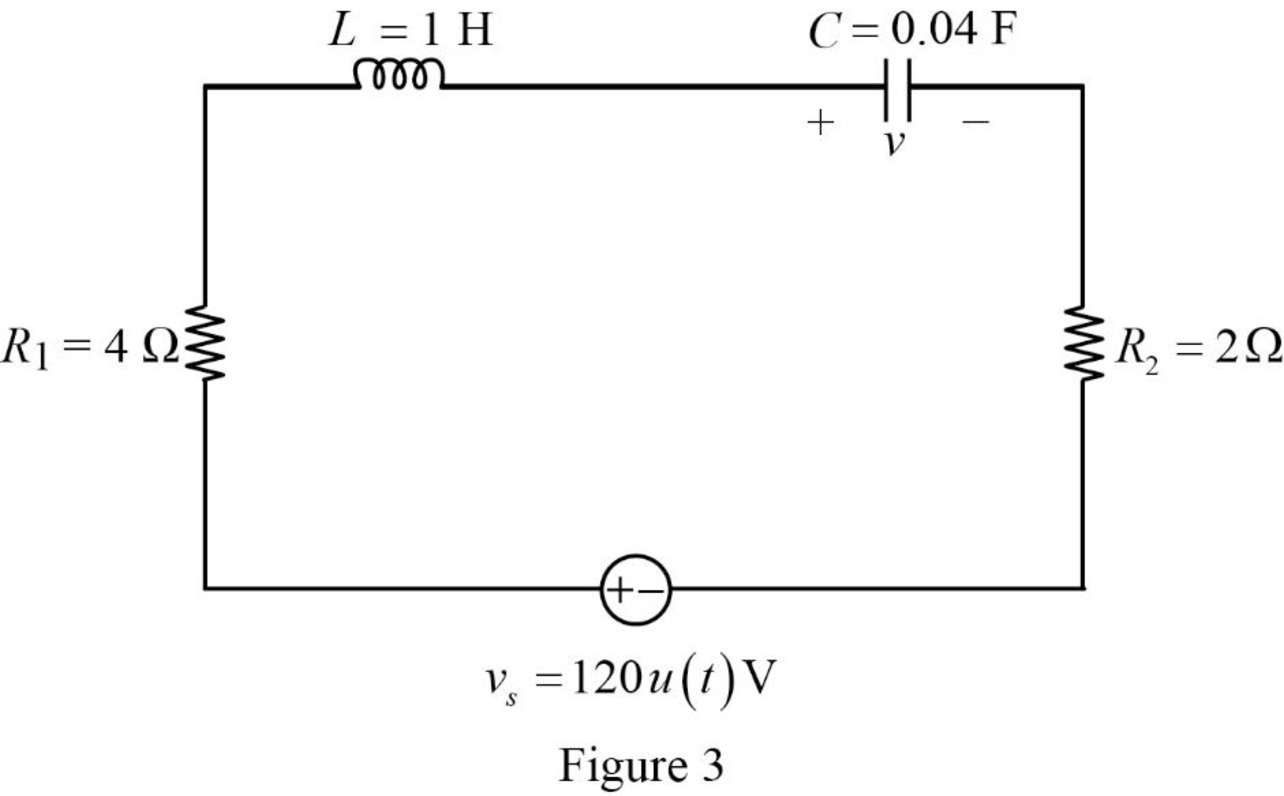
Substitute $4\Omega$ for $R_1$ in equation (1) to find $Z_{R_1}$.

$Z_{R_1}=4$

Substitute $2\Omega$ for $R_2$ in equation (1) to find $Z_{R_2}$.

$Z_{R_2}=2$

Substitute $1\text{H}$ for $L$ in equation (2) to find $Z_L$.

$\begin{array}{c}{Z}_L=s\left(1\text{H}\right)\\ =s\end{array}$

Substitute $0.04\text{F}$ for $C$ in equation (3) to find $Z_C$.

$\begin{array}{c}{Z}_C=\frac{1}{s\left(0.04\text{F}\right)}\\ =\frac{25}{s}\end{array}$

Apply Laplace transform for $v_s\left(t\right)$ to find $V_s\left(s\right)$.

$V_s\left(s\right)=\frac{120}{s}$

Using element transformation methods with initial conditions convert the Figure 3 into s-domain.

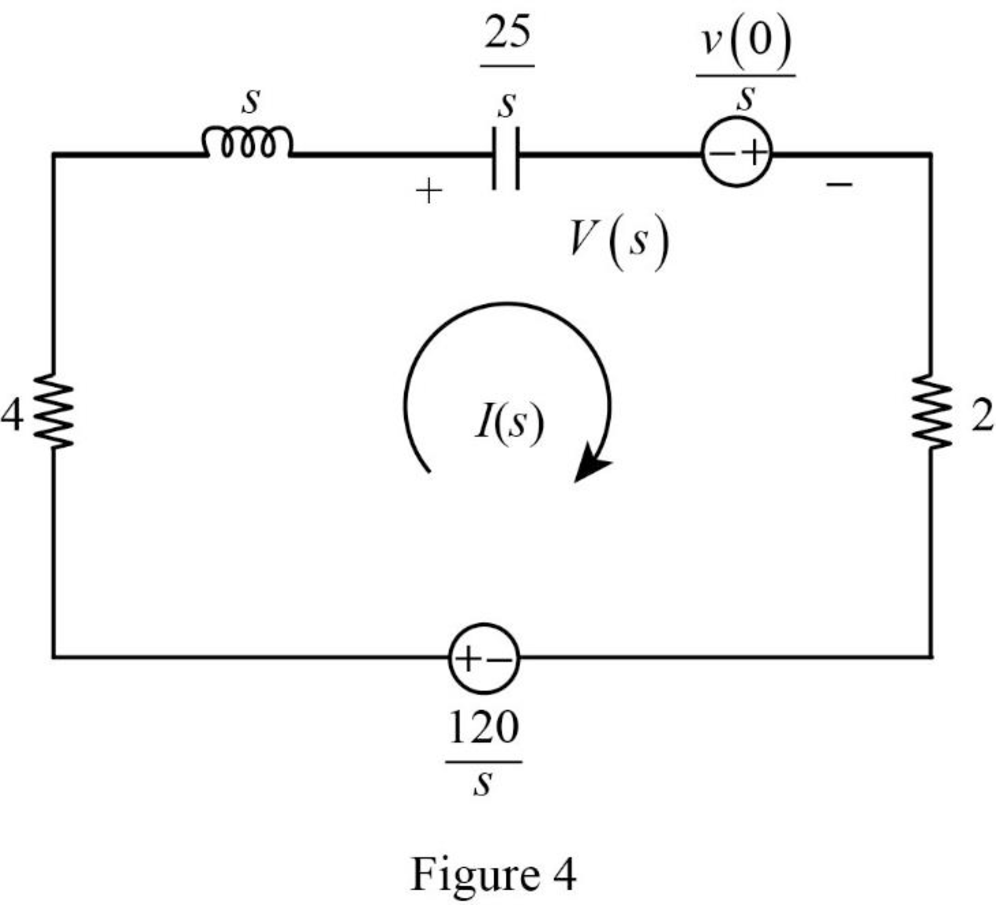
Apply Kirchhoff’s voltage law for the circuit shown in Figure 4.

$\begin{array}{l}4I\left(s\right)+sI\left(s\right)+\frac{25}{s}I\left(s\right)+\frac{v\left(0\right)}{s}+2I\left(s\right)-\frac{120}{s}=0\\ 6I\left(s\right)+sI\left(s\right)+\frac{25}{s}I\left(s\right)=-\frac{v\left(0\right)}{s}+\frac{120}{s}\\ I\left(s\right)\left[6+s+\frac{25}{s}\right]=-\frac{v\left(0\right)}{s}+\frac{120}{s}\\ I\left(s\right)\left[\frac{6s+s^2+25}{s}\right]=-\frac{v\left(0\right)}{s}+\frac{120}{s}\end{array}$

Substitute $-28.8$ for $v\left(0\right)$ in above equation.

$\begin{array}{l}I\left(s\right)\left[\frac{6s+s^2+25}{s}\right]=-\frac{\left(-28.8\right)}{s}+\frac{120}{s}\\ I\left(s\right)\left[\frac{s^2+6s+25}{s}\right]=\frac{28.8}{s}+\frac{120}{s}\\ I\left(s\right)\left[\frac{s^2+6s+25}{s}\right]=\frac{148.8}{s}\end{array}$

Simplify the above equation to find $I\left(s\right)$.

$I\left(s\right)=\frac{148.8}{s}\left(\frac{s}{s^2+6s+25}\right)$

$I\left(s\right)=\frac{148.8}{s^2+6s+25}$ (4)

From the equation (4), the characteristic equation is

$s^2+4s+25=0$ (5)

Write a general expression to calculate the roots of quadratic equation $\left(a{s}^2+bs+c=0\right)$.

$s_{1,2}=\frac{-b\pm \sqrt{b^2-4ac}}{2a}$ (6)

Comparing the equation (5) with the equation $\left(a{s}^2+bs+c=0\right)$.

$\begin{array}{l}a=1\\ b=6\\ c=25\end{array}$

Substitute $1$ for $a$, $6$ for $b$, and $25$ for $c$ in equation (6) to find $s_{1,2}$.

$\begin{array}{c}{s}_{1,2}=\frac{-6\pm \sqrt{{\left(6\right)}^2-4\left(1\right)\left(25\right)}}{2\left(1\right)}\\ =\frac{-6\pm \sqrt{36-100}}{2\left(1\right)}\\ =\frac{-6\pm \sqrt{-64}}{2}\\ =\frac{-6\pm j8}{2}\end{array}$

Simplify the above equation to find $s_{1,2}$.

$\begin{array}{c}{s}_{1,2}=\frac{-6+j8}{2},\frac{-6-j8}{2}\\ =-3+j4,-3-j4\end{array}$

Substitute the roots of characteristic equation in equation (4) to find $I\left(s\right)$.

$\begin{array}{c}I\left(s\right)=\frac{148.8}{\left(s-\left(-3+j4\right)\right)\left(\left(s-\left(-3-j4\right)\right)\right)}\\ =\frac{148.8}{\left(s-\left(-3+j4\right)\right)\left(s-\left(-3-j4\right)\right)}\end{array}$

Refer to Figure 4, the voltage $V\left(s\right)$ is calculated as follows:

$V\left(s\right)=\frac{25}{s}I\left(s\right)+\frac{v\left(0\right)}{s}$

Substitute $\frac{148.8}{\left(s-\left(-3+j4\right)\right)\left(s-\left(-3-j4\right)\right)}$ for $I\left(s\right)$, and $-28.8$ for $v\left(0\right)$ in above equation to find $V\left(s\right)$.

$V\left(s\right)=\frac{25}{s}\left[\frac{148.8}{\left(s-\left(-3+j4\right)\right)\left(s-\left(-3-j4\right)\right)}\right]-\frac{28.8}{s}$

$V\left(s\right)=\frac{3720}{s\left(s-\left(-3+j4\right)\right)\left(s-\left(-3-j4\right)\right)}-\frac{28.8}{s}$ (7)

Assume,

$V_1\left(s\right)=\frac{3720}{s\left(s-\left(-3+j4\right)\right)\left(s-\left(-3-j4\right)\right)}$ (8)

Substitute equation (8) in equation (7).

$V\left(s\right)=V_1\left(s\right)-\frac{28.8}{s}$ (9)

Take partial fraction for equation (8).

$V_1\left(s\right)=\frac{3720}{s\left(s-\left(-3+j4\right)\right)\left(s-\left(-3-j4\right)\right)}=\frac{A}{s}+\frac{B}{\left(s-\left(-3+j4\right)\right)}+\frac{C}{\left(s-\left(-3-j4\right)\right)}$ . (10)

The equation (10) can also be written as follows:

$\frac{3720}{s\left(s-\left(-3+j4\right)\right)\left(s-\left(-3-j4\right)\right)}=\frac{\left[\begin{array}{l}A\left(s-\left(-3+j4\right)\right)\left(s-\left(-3-j4\right)\right)+Bs\left(\left(s-\left(-3-j4\right)\right)\right)\\ +Cs\left(s-\left(-3+j4\right)\right)\end{array}\right]}{s\left(s-\left(-3+j4\right)\right)\left(s-\left(-3-j4\right)\right)}$

Simplify the above equation as follows:

$3720=\left[\begin{array}{l}A\left(s-\left(-3+j4\right)\right)\left(s-\left(-3-j4\right)\right)+Bs\left(\left(s-\left(-3-j4\right)\right)\right)\\ +Cs\left(s-\left(-3+j4\right)\right)\end{array}\right]$ (11)

Substitute $0$ for $s$ in equation (11) to find $A$.

$\begin{array}{l}3720=A\left(0-\left(-3+j4\right)\right)\left(0-\left(-3-j4\right)\right)+B\left(0\right)\left(\left(0-\left(-3-j4\right)\right)\right)+C\left(0\right)\left(0-\left(-3+j4\right)\right)\\ 3720=A\left(3-j4\right)\left(3+j4\right)+0+0\\ 3720=A\left(3^2-{\left(j4\right)}^2\right)\left\{\because a^2-b^2=\left(a+b\right)\left(a-b\right)\right\}\\ 3720=A\left(9-j^{2}16\right)\end{array}$

Simplify the above equation to find $A$.

$\begin{array}{c}A=\frac{3720}{9-j^{2}16}\\ =\frac{3720}{9-\left(-1\right)16}\left\{\because j^2=-1\right\}\\ =\frac{3720}{25}\\ =148.8\end{array}$

Substitute $-3+j4$ for $s$ in equation (11) to find $B$.

$\begin{array}{l}3720=\left[\begin{array}{l}A\left(\left(-3+j4\right)-\left(-3+j4\right)\right)\left(\left(-3+j4\right)-\left(-3-j4\right)\right)\\ +B\left(-3+j4\right)\left(\left(\left(-3+j4\right)-\left(-3-j4\right)\right)\right)\\ +C\left(-3+j4\right)\left(\left(-3+j4\right)-\left(-3+j4\right)\right)\end{array}\right]\\ 3720=A\left(0\right)+B\left(-3+j4\right)\left(j8\right)+C\left(0\right)\\ 3720=B\left(-32-j24\right)\end{array}$

Simplify the above equation to find $B$.

$\begin{array}{c}B=\frac{3720}{-32-j24}\\ =93\angle 143.13°\end{array}$

Substitute $-3-j4$ for $s$ in equation (11) to find $B$.

$\begin{array}{l}3720=\left[\begin{array}{l}A\left(\left(-3-j4\right)-\left(-3+j4\right)\right)\left(\left(-3-j4\right)-\left(-3-j4\right)\right)\\ +B\left(-3-j4\right)\left(\left(\left(-3-j4\right)-\left(-3-j4\right)\right)\right)\\ +C\left(-3-j4\right)\left(\left(-3-j4\right)-\left(-3+j4\right)\right)\end{array}\right]\\ 3720=A\left(0\right)+B\left(0\right)+C\left(-3-j4\right)\left(-j8\right)\\ 3720=C\left(-32+j24\right)\end{array}$

Simplify the above equation to find $B$.

$\begin{array}{c}C=\frac{3720}{-32+j24}\\ =93\angle -143.13°\end{array}$

Substitute $148.8$ for $A$, $93\angle 143.13°$ for $B$, and $93\angle -143.13°$ for $C$ in equation (10) to find $V_1\left(s\right)$.

$V_1\left(s\right)=\frac{148.8}{s}+\frac{93\angle 143.13°}{\left(s-\left(-3+j4\right)\right)}+\frac{93\angle -143.13°}{\left(s-\left(-3-j4\right)\right)}$

Substitute $\frac{148.8}{s}+\frac{93\angle 143.13°}{\left(s-\left(-3+j4\right)\right)}+\frac{93\angle -143.13°}{\left(s-\left(-3-j4\right)\right)}$ for $V_1\left(s\right)$ in equation (9) to find $V\left(s\right)$.

$\begin{array}{c}V\left(s\right)=\frac{148.8}{s}+\frac{93\angle 143.13°}{\left(s-\left(-3+j4\right)\right)}+\frac{93\angle -143.13°}{\left(s-\left(-3-j4\right)\right)}-\frac{28.8}{s}\\ =\frac{120}{s}+\frac{93\angle 143.13°}{\left(s-\left(-3+j4\right)\right)}+\frac{93\angle -143.13°}{\left(s-\left(-3-j4\right)\right)}\\ =\left[\begin{array}{c}\frac{120}{s}+\frac{93\left(\cos \left(143.13°\right)+\sin \left(143.13°\right)\right)}{\left(s-\left(-3+j4\right)\right)}\\ +\frac{93\left(\cos \left(-143.13\right)°+\sin \left(-143.13\right)°\right)}{\left(s-\left(-3-j4\right)\right)}\end{array}\right]\\ =\frac{120}{s}+\frac{93e^{j\left(143.13°\right)}}{\left(s-\left(-3+j4\right)\right)}+\frac{93e^{j\left(-143.13°\right)}}{\left(s-\left(-3-j4\right)\right)}\left\{\because e^{i\theta }=\cos \theta +i\sin \theta \right\}\end{array}$

Apply inverse Laplace transform for above equation to find $v\left(t\right)$.

$\begin{array}{c}v\left(t\right)=\left[\begin{array}{c}120u\left(t\right)+93e^{j\left(143.13°\right)}{e}^{\left(-3+j4\right)t}u\left(t\right)\\ +93e^{j\left(-143.13°\right)}{e}^{\left(-3-j4\right)t}u\left(t\right)\end{array}\right]\left\{\because {\mathcal{L}}^{-1}\left(\frac{1}{s+a}\right)=e^{-at}u\left(t\right)\right\}\\ =\left[120+93e^{\left(-3t+j4t+j\mathrm{14.3.13}°\right)}+93e^{\left(-3t-j4t-j143.13°\right)}\right]u\left(t\right)\left\{\because e^a\cdot e^b=e^{a+b}\right\}\\ =\left[120+93e^{-3t}{e}^{j\left(4t+\mathrm{14.3.13}°\right)}+93e^{-3t}{e}^{-j}{}^{\left(4t+143.13°\right)}\right]u\left(t\right)\\ =\left[120+93e^{-3t}\left[e^{j\left(4t+\mathrm{14.3.13}°\right)}+e^{-j}{}^{\left(4t+143.13°\right)}\right]\right]u\left(t\right)\end{array}$

Simplify the above equation to find $v\left(t\right)$.

$\begin{array}{c}v\left(t\right)=\left[120+93e^{-3t}\left[e^{j\left(4t+\mathrm{14.3.13}°\right)}+e^{-j}{}^{\left(4t+143.13°\right)}\right]\right]u\left(t\right)\\ =\left[120+93e^{-3t}\left[2\cos \left(4t+143.13°\right)\right]\right]u\left(t\right)\left\{\because \cos \theta =\frac{e^{i\theta }+e^{-i\theta }}{2}\right\}\\ =\left[120+186e^{-3t}\cos \left(4t+143.13°\right)\right]u\left(t\right)\text{V}\end{array}$

Conclusion:

Thus, the expression of voltage $v\left(t\right)$ for $t>0$ in the circuit of Figure 16.51 is $\left[120+186e^{-3t}\cos \left(4t+143.13°\right)\right]u\left(t\right)\text{V}$.