
(a)
To Find: The congruent segment.
(a)
Answer to Problem 6RP
Explanation of Solution
Given:
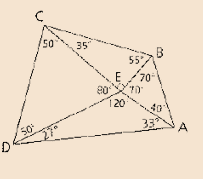
Formula Used:
In a
Calculation:
Conclusion:
Thus the required congruent segments are
(b)
To Find: The requiredshorter segment in the given figure.
(b)
Answer to Problem 6RP
Explanation of Solution
Given:
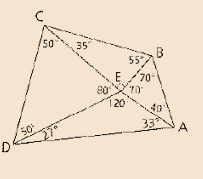
Formula Used:
In a triangle side opposite to greater angle is always greater and opposite to smallest angel is always smallest or vice-versa.
Angle-Sum Property: In a triangle the sum of all interior angle is equal to 180.
Calculation:
Conclusion:
Thus the required segment is
(c)
To Define: The name of the required segment.
(c)
Answer to Problem 6RP
Hypotenuse
Explanation of Solution
Given:
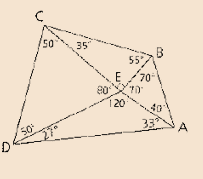
Formula Used:
Pythagorean-Theorem: It states that in right angled triangle the longest segment is termed as Hypotenuse.
Calculation:
Conclusion:
Thus the name of required segment is Hypotenuse.
(d)
To Find: The required longer segment in the given figure.
(d)
Answer to Problem 6RP
Explanation of Solution
Given:
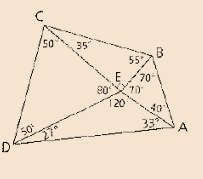
Formula Used:
In a triangle side opposite to greater angle is always greater and opposite to smallest angel is always smallest or vice-versa.
Angle-Sum Property: In a triangle the sum of all interior angle is equal to 180.
Calculation:
Conclusion:
Thus the required segment is
(b)
To Find: The required shortest segment in the given figure.
(b)
Answer to Problem 6RP
Explanation of Solution
Given:
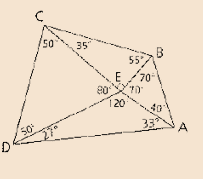
Formula Used:
In a triangle side opposite to greater angle is always greater and opposite to smallest angel is always smallest or vice-versa.
Angle-Sum Property: In a triangle the sum of all interior angle is equal to 180.
Calculation:
Conclusion:
Thus the required segment is
Chapter 15 Solutions
Geometry For Enjoyment And Challenge
Additional Math Textbook Solutions
Elementary Statistics: Picturing the World (7th Edition)
University Calculus: Early Transcendentals (4th Edition)
Thinking Mathematically (6th Edition)
Elementary Statistics
Elementary Statistics (13th Edition)
Calculus: Early Transcendentals (2nd Edition)
- Find the area of a square whose diagonal is 10arrow_forwardDecomposition geometry: Mary is making a decorative yard space with dimensions as shaded in green (ΔOAB).Mary would like to cover the yard space with artificial turf (plastic grass-like rug). Mary reasoned that she could draw a rectangle around the figure so that the point O was at a vertex of the rectangle and that points A and B were on sides of the rectangle. Then she reasoned that the three smaller triangles resulting could be subtracted from the area of the rectangle. Mary determined that she would need 28 square meters of artificial turf to cover the green shaded yard space pictured exactly.arrow_forward7. 11 m 12.7 m 14 m S V=B₁+ B2(h) 9.5 m 16 m h+s 2 na 62-19 = 37 +, M h² = Bu-29arrow_forward
- 39 Two sides of one triangle are congruent to two sides of a second triangle, and the included angles are supplementary. The area of one triangle is 41. Can the area of the second triangle be found?arrow_forwardA parallelogram with an area of 211.41 m^2 hast a base Thatcher measures 24.3m. Find ist height.arrow_forwardBH is tangent to circle A and DF is a diameter. I don't know where to go from here. May you help please?arrow_forward
 Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage, Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning
Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning

