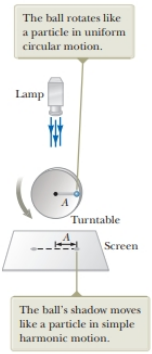
Problem 15.1QQ: A block on the end of a spring is pulled to position x = A and released from rest. In one full cycle... Problem 15.2QQ: Consider a graphical representation (Fig. 15.3) of simple harmonic motion as described... Problem 15.3QQ: Figure 15.4 shows two curves representing particles undergoing simple harmonic motion. The correct... Problem 15.4QQ: An object of mass m is hung from a spring and set into oscillation. The period of the oscillation is... Problem 15.5QQ: The ball in Figure 15.13 moves in a circle of radius 0.50 m. At t = 0, the ball is located on the... Problem 15.6QQ: The grandfather clock in the opening storyline depends on the period of a pendulum to keep correct... Problem 15.1OQ: If a simple pendulum oscillates with small amplitude and its length is doubled, what happens to the... Problem 15.2OQ: You attach a block to the bottom end of a spring hanging vertically. You slowly let the block move... Problem 15.3OQ: A block-spring system vibrating on a frictionless, horizontal surface with an amplitude of 6.0 cm... Problem 15.4OQ: An object-spring system moving with simple harmonic motion has an amplitude A. When the kinetic... Problem 15.5OQ: An object of mass 0.40 kg, hanging from a spring with a spring constant of 8.0 N/m, is set into an... Problem 15.6OQ: A runaway railroad car, with mass 3.0 105 kg, coasts across a level track at 2.0 m/s when it... Problem 15.7OQ: The position of an object moving with simple harmonic motion is given by x = 4 cos (6t), where x is... Problem 15.8OQ: If an object of mass m attached to a light spring is replaced by one of mass 9m, the frequency of... Problem 15.9OQ: You stand on the end of a diving board and bounce to set it into oscillation. You find a maximum... Problem 15.10OQ: A mass-spring system moves with simple harmonic motion along the x axis between turning points at x1... Problem 15.11OQ: A block with mass m = 0.1 kg oscillates with amplitude .A = 0.1 in at the end of a spring with force... Problem 15.12OQ: For a simple harmonic oscillator, answer yes or no to the following questions, (a) Can the... Problem 15.13OQ: The top end of a spring is held fixed. A block is hung on the bottom end as in Figure OQ15.13a, and... Problem 15.14OQ: Which of the following statements is not true regarding a mass-spring system that moves with simple... Problem 15.15OQ: A simple pendulum has a period of 2.5 s. (i) What is its period if its length is made four times... Problem 15.16OQ: A simple pendulum is suspended from the ceiling of a stationary elevator, and the period is... Problem 15.17OQ: A particle on a spring moves in simple harmonic motion along the x axis between turning points at x1... Problem 15.1CQ: You are looking at a small, leafy tree. You do not notice any breeze, and most of the leaves on the... Problem 15.2CQ Problem 15.3CQ: If the coordinate of a particle varies as x = -A cos t, what is the phase constant in Equation 15.6?... Problem 15.4CQ: A pendulum bob is made from a sphere filled with water. What would happen to the frequency of... Problem 15.5CQ: Figure CQ15.5 shows graphs of the potential energy of four different systems versus the position of... Problem 15.6CQ: A student thinks that any real vibration must be damped. Is the student correct? If so, give... Problem 15.7CQ: The mechanical energy of an undamped block-spring system is constant as kinetic energy transforms to... Problem 15.8CQ: Is it possible to have damped oscillations when a system is at resonance? Explain. Problem 15.9CQ: Will damped oscillations occur for any values of b and k? Explain. Problem 15.10CQ: If a pendulum clock keeps perfect time al the base of a mountain, will it also keep perfect time... Problem 15.11CQ Problem 15.12CQ: A simple pendulum can be modeled as exhibiting simple harmonic motion when is small. Is the motion... Problem 15.13CQ: Consider the simplified single-piston engine in Figure CQ15.13. Assuming the wheel rotates with... Problem 15.1P: A 0.60-kg block attached to a spring with force constant 130 N/m is free to move on a frictionless,... Problem 15.2P: When a 4.25-kg object is placed on lop of a vertical spring, the spring compresses a distance of... Problem 15.3P: A vertical spring stretches 3.9 cm when a 10-g object is tiling from it. The object is replaced with... Problem 15.4P: In an engine, a piston oscillates with simpler harmonic motion so that its position varies according... Problem 15.5P: The position of a particle is given by the expression x = 4.00 cos {3.00 t + }, where x is in meters... Problem 15.6P: A piston in a gasoline engine is in simple harmonic motion. The engine is running at the rate of 3... Problem 15.7P: A 1.00-kg object is attached to a horizontal spring. The spring is initially stretched by 0.100 m,... Problem 15.8P: A simple harmonic oscillator takes 12.0 s to undergo five complete vibrations. Find (a) the period... Problem 15.9P: A 7.00-kg object is hung from the bottom end of a vertical spring fastened to an overhead beam. The... Problem 15.10P: At an outdoor market, a bunch of bananas attached to the bottom of a vertical spring of force... Problem 15.11P: A vibration sensor, used in testing a washing machine consists of a cube of aluminum 1.50 cm on edge... Problem 15.12P: (a) A hanging spring stretches by 35.0 cm when an object of mass 450 g is hung on it at rest. In... Problem 15.13P: Review. A particle moves along the x axis. It is initially at the position 0.270 m, moving with... Problem 15.14P: A ball dropped from a height of 4.00 m makes an elastic collision with the ground. Assuming no... Problem 15.15P: A particle moving along the x axis in simple harmonic motion starts from its equilibrium position,... Problem 15.16P: The initial position, velocity, and acceleration of an object moving in simple harmonic motion are... Problem 15.17P: A particle moves in simple harmonic motion with a frequency of 3.00 Hz and an amplitude of 5.00 cm.... Problem 15.18P: A 1.00-kg glider attached to a spring with a force constant of 25.0 N/m oscillates on a... Problem 15.19P: A 0.500-kg object attached to a spring with a force constant of 8.00 N/m vibrates in simple harmonic... Problem 15.20P: You attach an object to the bottom end of a hanging vertical spring. It hangs at rest alter... Problem 15.21P: To test the resiliency of its bumper during low-speed collisions, a 1 000-kg automobile is driven... Problem 15.22P: A 200-g block is attached to a horizontal spring and executes simple harmonic motion with a period... Problem 15.23P: A block of unknown mass is attached to a spring with a spring constant of 6.50 N/m and undergoes... Problem 15.24P: A block-spring system oscillates with an amplitude of 3.50 cm. The spring constant is 250 N/m and... Problem 15.25P: A particle executes simple harmonic motion with an amplitude of 3.00 cm. At what position does its... Problem 15.26P: The amplitude of a system moving in simple harmonic motion is doubled. Determine the change in (a)... Problem 15.27P: A 50.0-g object connected to a spring with a force constant of 35.0 N/m oscillates with an amplitude... Problem 15.28P: A 2.00-kg object is attached to a spring and placed on a frictionless, horizontal surface. A... Problem 15.29P: A simple harmonic oscillator of amplitude A has a total energy Determine E, (a) the kinetic energy... Problem 15.30P: Review. A 65.0-kg bungee jumper steps off a bridge with a light bungee cord tied to her body and to... Problem 15.31P: Review. A 0.250-kg block resting on a frictionless, horizontal surface is attached to a spring whose... Problem 15.32P Problem 15.33P: While driving behind a car traveling at 3.00 m/s, you notice that one of the cars tires has a small... Problem 15.34P: A seconds pendulum is one that moves through its equilibrium position once each second. (The period... Problem 15.35P: A simple pendulum makes 120 complete oscillations in 3.00 min at a location where g = 9.80 m/s2.... Problem 15.36P: A particle of mass m slides without friction inside a hemispherical bowl of radius R. Show that if... Problem 15.37P: A physical pendulum in the form of a planar object moves in simple harmonic motion with a frequency... Problem 15.38P: A physical pendulum in the form of a planar object moves in simple harmonic motion with a frequency... Problem 15.39P: The angular position of a pendulum is represented by the equation = 0.032 0 cos t, where is in... Problem 15.40P: Consider the physical pendulum of Figure 15.16. (a) Represent its moment of inertia about an axis... Problem 15.41P Problem 15.42P: A very light rigid rod of length 0.500 m extends straight out from one end of a meterstick. The... Problem 15.43P: Review. A simple pendulum is 5.00 m long. What is the period of small oscillations for this pendulum... Problem 15.44P: A small object is attached to the end of a string to form a simple pendulum. The period of its... Problem 15.45P: A watch balance wheel (Fig. P15.25) has a period of oscillation of 0.250 s. The wheel is constructed... Problem 15.46P: A pendulum with a length of 1.00 m is released from an initial angle of 15.0. After 1 000 s, its... Problem 15.47P: A 10.6-kg object oscillates at the end of a vertical spring that has a spring constant of 2.05 104... Problem 15.48P: Show that the time rate of change of mechanical energy for a damped, undriven oscillator is given by... Problem 15.49P: Show that Equation 15.32 is a solution of Equation 15.31 provided that b2 4 mk. Problem 15.50P: A baby bounces up and down in her crib. Her mass is 12.5 kg, and the crib mattress can be modeled as... Problem 15.51P: As you enter a fine restaurant, you realize that you have accidentally brought a small electronic... Problem 15.52P: A block weighing 40.0 N is suspended from a spring that has a force constant of 200 N/m. The system... Problem 15.53P: A 2.00-kg object attached to a spring moves without friction (b = 0) and is driven by an external... Problem 15.54P: Considering an undamped, forced oscillator (b = 0), show that Equation 15.35 is a solution of... Problem 15.55P: Damping is negligible for a 0.150-kg object hanging from a light, 6.30-N/m spring. A sinusoidal... Problem 15.56AP: The mass of the deuterium molecule (D2) is twice that of the hydrogen molecule (H2). If the... Problem 15.57AP: An object of mass m moves in simple harmonic motion with amplitude 12.0 cm on a light spring. Its... Problem 15.58AP: Review. This problem extends the reasoning of Problem 41 in Chapter 9. Two gliders are set in motion... Problem 15.59AP: A small ball of mass M is attached to the end of a uniform rod of equal mass M and length L that is... Problem 15.60AP: Review. A rock rests on a concrete sidewalk. An earthquake strikes, making the ground move... Problem 15.61AP: Four people, each with a mass of 72.4 kg, are in a car with a mass of 1 130 kg. An earthquake... Problem 15.62AP: To account for the walking speed of a bipedal or quadrupedal animal, model a leg that is not... Problem 15.63AP Problem 15.64AP: An object attached to a spring vibrates with simple harmonic motion as described by Figure P15.33.... Problem 15.65AP: Review. A large block P attached to a light spring executes horizontal, simple harmonic motion as it... Problem 15.66AP: Review. A large block P attached to a light spring executes horizontal, simple harmonic motion as it... Problem 15.67AP: A pendulum of length L and mass M has a spring of force constant k connected to it at a distance h... Problem 15.68AP: A block of mass m is connected to two springs of force constants k1 and k2 in two ways as shown in... Problem 15.69AP: A horizontal plank of mass 5.00 kg and length 2.00 m is pivoted at one end. The planks other end is... Problem 15.70AP: A horizontal plank of mass m and length L is pivoted at one end. The planks other end is supported... Problem 15.71AP: Review. A particle of mass 4.00 kg is attached to a spring with a force constant of 100 N/m. It is... Problem 15.72AP: A ball of mass m is connected to two rubber bands of length L, each under tension T as shown in... Problem 15.73AP: Review. One end of a light spring with force constant k = 100 N/m is attached to a vertical wall. A... Problem 15.74AP: People who ride motorcycles and bicycles learn to look out for bumps in the road and especially for... Problem 15.75AP: A simple pendulum with a length of 2.23 m and a mass of 6.74 kg is given an initial speed of 2.06... Problem 15.76AP: When a block of mass M, connected to the end of a spring of mass ms = 7.40 g and force constant k,... Problem 15.77AP: Review. A light balloon filled with helium of density 0.179 kg/m3 is tied to a light string of... Problem 15.78AP: Consider the damped oscillator illustrated in Figure 15.19. The mass of the object is 375 g, the... Problem 15.79AP: A particle with a mass of 0.500 kg is attached to a horizontal spring with a force constant of 50.0... Problem 15.80AP: Your thumb squeaks on a plate you have just washed. Your sneakers squeak on the gym floor. Car tires... Problem 15.81AP: Review. A lobstermans buoy is a solid wooden cylinder of radius r and mass M. It is weighted at one... Problem 15.82AP Problem 15.83AP: Two identical steel balls, each of mass 67.4 g, are moving in opposite directions at 5.00 m/s. They... Problem 15.84CP: A smaller disk of radius r and mass m is attached rigidly to the face of a second larger disk of... Problem 15.85CP: An object of mass m1 = 9.00 kg is in equilibrium when connected to a light spring of constant k =... Problem 15.86CP: Review. Why is the following situation impassible? You are in the high-speed package delivers... Problem 15.87CP: A block of mass M is connected to a spring of mass m and oscillates in simple harmonic motion on a... Problem 15.88CP: Review. A system consists of a spring with force constant k = 1 250 N/m, length L = 1.50 m, and an... Problem 15.89CP: A light, cubical container of volume a3 is initially filled with a liquid of mass density as shown... format_list_bulleted


 Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning Classical Dynamics of Particles and SystemsPhysicsISBN:9780534408961Author:Stephen T. Thornton, Jerry B. MarionPublisher:Cengage Learning
Classical Dynamics of Particles and SystemsPhysicsISBN:9780534408961Author:Stephen T. Thornton, Jerry B. MarionPublisher:Cengage Learning University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University
University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning




