Chapter 15, Problem 109PP

Doughnuts are cooked by dropping the dough into hot vegetable oil until it changes from white to a rich, golden brown. One popular brand of doughnut automates this process; the doughnuts are made on an assembly line that customers can view in operation as they wait to order. Watching the doughnuts cook gives the customers time to develop an appetite as they ponder the physics of the process.

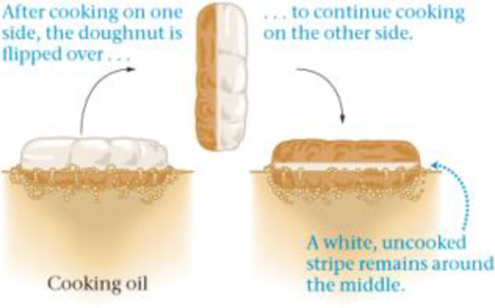
First, the uncooked doughnut is dropped into hot vegetable oil, whose density is ρ = 919 kg/m³. There it browns on one side as it floats on the oil. After cooking for the proper amount of time, a mechanical lever flips the doughnut over so it can cook on the other side. The doughnut floats fairly high in the oil, with less than half of its volume submerged. As a result, the final product has a characteristic white stripe around the middle where the dough is always out of the oil, as shown in Figure 15-54.

Figure 15-54 Steps in cooking a doughnut

The relationship between the density of the doughnut and the height of the white stripe is graphed in Figure 15-55. On the x axis we plot the density of the doughnut as a fraction of the density of the vegetable cooking oil; the y axis shows the height of the white stripe as a fraction of the total height of the doughnut. Notice that the height of the white stripe is plotted for both positive and negative values.

Figure 15-55 Cooking a floating doughnut

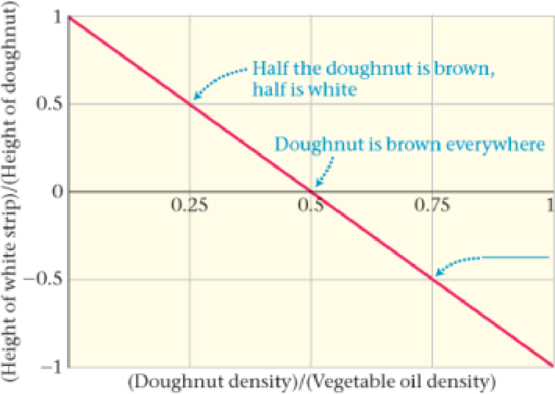
109. •• A new doughnut is being planned whose density will be 330 kg/m³. If the height of the doughnut is H, what will be the height of the white stripe?

1. A. 0.14H
2. B. 0.24H
3. C. 0.28H
4. D. 0.64H