Chapter 14.5, Problem 24E

The data from exercise 2 follow.

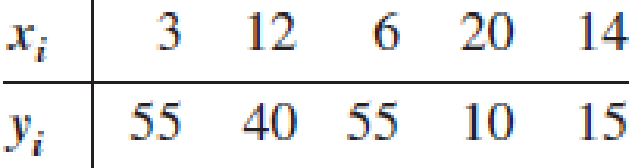
1. a. Compute the mean square error using equation (14.15).
2. b. Compute the standard error of the estimate using equation (14.16).
3. c. Compute the estimated standard deviation of b₁ using equation (14.18).
4. d. Use the t test to test the following hypotheses (α = .05):

$\begin{array}{l}{H}_0:{\beta }_1=0\\ H_a:{\beta }_1\ne 0\end{array}$

1. e. Use the F test to test the hypotheses in part (d) at a .05 level of significance. Present the results in the analysis of variance table format.