
To solve: The function is defined on the interval ,
a. Graph .
indicating the area under from 0 to 4.
Answer to Problem 15AYU
a.
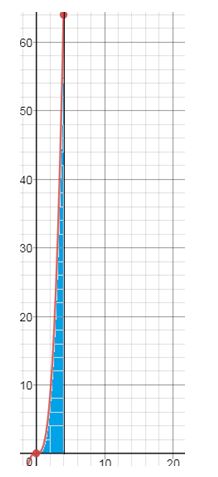
Explanation of Solution
Given:
The function is defined on the interval .
Calculation:
a. Graph
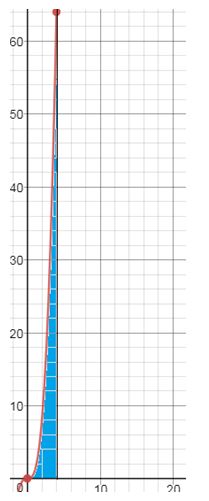
To solve: The function is defined on the interval ,
b. Approximate the area by Partition into four subintervals of equal length and choose as the left endpoint of each subinterval.
Answer to Problem 15AYU
b. 36
Explanation of Solution
Given:
The function is defined on the interval .
Calculation:
b. Partition into four subintervals of equal length 1 and choose as the left endpoint of each subinterval.
The area is approximated as
To solve: The function is defined on the interval ,
c. Approximate the area by Partition into eight subintervals of equal length and choose as the left endpoint of each subinterval.
Answer to Problem 15AYU
c. 49
Explanation of Solution
Given:
The function is defined on the interval .
Calculation:
c. Partition into eight subintervals of equal length and choose as the left endpoint of each subinterval.
The area is approximated as
To solve: The function is defined on the interval ,
d. Express the area as an integral.
Answer to Problem 15AYU
d.
Explanation of Solution
Given:
The function is defined on the interval .
Calculation:
d. Express the area as an integral.
The area as an integral is
To solve: The function is defined on the interval ,
e. Use a graphing utility to approximate the integral.
Answer to Problem 15AYU
e. 64
Explanation of Solution
Given:
The function is defined on the interval .
Calculation:
e. Use a graphing utility to approximate the integral.
That is evaluate the integral.
The value of the integral is 64, so the area under the graph of from 0 to 4 is 64.
Chapter 14 Solutions
Precalculus Enhanced with Graphing Utilities
Additional Math Textbook Solutions
Precalculus
Calculus: Early Transcendentals (2nd Edition)
Algebra and Trigonometry (6th Edition)
University Calculus: Early Transcendentals (4th Edition)
College Algebra with Modeling & Visualization (5th Edition)
College Algebra (7th Edition)
- The graph of f' is below. Use it to determine where the local minima and maxima for f are. If there are multiple answers, separate with commas. 2 f'(x) N -5 -4 3-2-1 -1 -2 -3 -4 12 3 4 5 -x Local minima at x Local maxima at xarrow_forwardThe graph of f' is below. Use it to determine the intervals where f is increasing. -5-4-32 4- 3 2 1 -2 -3 +x 2 3 4 5arrow_forwardThe graph of f' is below. Use it to determine where the inflection points are and the intervals where f is concave up and concave down. If there are multiple inflection points, separate with a comma. 6 5 4 3 2 1 f'(x) +x -6-5-4-3 -2 -1 1 2 3 4 5 6 -1 -2 -3 -4 -5 -6+ Inflection point(s) at x = Concave up: Concave down:arrow_forward
- The graph of f' is below. Use it to determine where the local minima and maxima for f are. If there are multiple answers, separate with commas. f'(x) 4- -5-4-3-8-1 3 2 1 x 1 2 3 4 5 -1 -2 -3 -4 Local minima at a Local maxima at =arrow_forwardThe graph of f' is below. Use it to determine the intervals where f is increasing. f'(xx) 4- -5 -3 -2 3 2 1 1 2 3 4 5 Cit +x 7 2arrow_forwardPlease focus on problem ii.arrow_forward
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





